Tensión superficial para niños
La tensión superficial de un líquido es como una capa elástica invisible que cubre su superficie. Esta capa hace que el líquido se resista a estirarse o a aumentar su tamaño. Gracias a ella, algunos insectos pueden caminar sobre el agua sin hundirse, como si la superficie fuera una cama elástica.
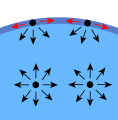
Esta "piel" elástica se forma porque las moléculas dentro de un líquido se atraen entre sí. Las moléculas en la superficie tienen menos vecinas con las que unirse que las que están en el interior, lo que crea una fuerza que las jala hacia adentro y hace que la superficie se contraiga.
La tensión superficial también es la razón por la que las gotas de agua son redondas: un círculo o una esfera es la forma que tiene la menor superficie para un volumen dado, y los líquidos siempre buscan minimizar su superficie para gastar la menor energía posible.
Contenido
¿Por qué ocurre la tensión superficial?
La tensión superficial ocurre por las fuerzas de atracción entre las moléculas de un líquido. Imagina que las moléculas son como pequeños imanes que se atraen.
Moléculas en el interior
Dentro del líquido, cada molécula está rodeada por otras moléculas que la jalan en todas direcciones. Estas fuerzas se equilibran, así que la molécula se siente cómoda y con poca energía.
Moléculas en la superficie
En la superficie, las moléculas no tienen otras moléculas por encima que las jalen. Solo tienen moléculas a los lados y hacia abajo. Esto crea una fuerza neta que las jala hacia el interior del líquido. Es como si quisieran meterse más adentro para estar rodeadas por más moléculas.
Para que el líquido tenga la menor energía posible, intenta que el número de moléculas en su superficie sea el mínimo. Por eso, la superficie se contrae y busca la forma más pequeña posible, como una esfera en el caso de una gota.
Propiedades de la tensión superficial
La tensión superficial tiene algunas características importantes:
- Siempre es positiva: Siempre se necesita energía para estirar la superficie de un líquido.
- Depende de los materiales: Su valor cambia según el tipo de líquido y con qué esté en contacto (aire, otro líquido, un sólido). Por ejemplo, el agua tiene una tensión superficial diferente si está en contacto con el aire o con aceite.
- Es una fuerza por longitud: Se mide como una fuerza que actúa a lo largo de una línea en la superficie.
- Fuerzas entre moléculas: Cuanto más fuertes sean las fuerzas que unen las moléculas de un líquido, mayor será su tensión superficial. Por ejemplo, el mercurio tiene una tensión superficial muy alta porque sus átomos se atraen fuertemente.
- Disminuye con la temperatura: Si calientas un líquido, sus moléculas se mueven más rápido y las fuerzas de atracción entre ellas se debilitan. Por eso, la tensión superficial disminuye a medida que la temperatura aumenta.
Efectos de la tensión superficial
La tensión superficial es la causa de muchos fenómenos que vemos a diario:
El agua y sus formas
- Gotas de lluvia: Cuando la lluvia cae sobre una superficie encerada (como una hoja), el agua no se pega bien a la cera, pero sí se atrae fuertemente a sí misma. Por eso, el agua se agrupa en gotas casi esféricas, ya que la esfera es la forma con la menor superficie para su volumen.
- Formación de gotas: Si dejas caer agua lentamente de un grifo, verás cómo se forma una gota. El agua se estira hasta que la tensión superficial no puede sostenerla más, se suelta y la tensión superficial la convierte en una esfera perfecta.
- Insectos sobre el agua: Algunos insectos, como los zapateros, pueden caminar sobre la superficie de un estanque. Sus patas no se mojan y su peso es tan ligero que la tensión superficial del agua los soporta. La superficie del agua se curva un poco bajo sus patas, como una cama elástica, y la fuerza de la tensión superficial los empuja hacia arriba.
- Separación de líquidos: La tensión superficial también explica por qué el aceite y el agua no se mezclan. Hay una tensión entre las superficies de los dos líquidos que los mantiene separados.

El papel de los jabones
- Burbujas de jabón: Las burbujas de agua pura son inestables y se rompen fácilmente. Pero si añades jabón (que son sustancias llamadas surfactantes), la tensión superficial del agua disminuye mucho. Esto permite que las burbujas sean estables y duren más tiempo.
- Emulsiones: Cuando intentas mezclar aceite y agua, el aceite se separa en grandes masas. Pero si añades un surfactante (como el jabón en la mayonesa), este reduce la tensión superficial y permite que el aceite se disperse en pequeñas gotas estables dentro del agua, formando una emulsión.
¿Cómo se mide la tensión superficial?
La tensión superficial se mide en unidades de fuerza por longitud, como Newtons por metro (N/m) o dinas por centímetro (dyn/cm). Un instrumento que la mide se llama tensiómetro.
Algunos métodos para medirla son:
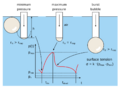
- Método del anillo de du Noüy: Se mide la fuerza máxima necesaria para levantar un anillo de la superficie del líquido.
- Método del platillo de Wilhelmy: Se usa un platillo vertical que se sumerge en el líquido y se mide la fuerza que ejerce la tensión superficial sobre él.
- Método de la gota colgante: Se analiza la forma de una gota que cuelga de una jeringa para calcular la tensión superficial.
- Método de elevación capilar: Se sumerge un tubo muy delgado (capilar) en el líquido y se mide la altura a la que el líquido sube dentro del tubo. Esta altura está relacionada con la tensión superficial.
Efectos en la vida diaria
Líquido en tubos delgados (capilaridad)
Si pones un tubo de vidrio muy delgado en agua, verás que el agua sube por el tubo, incluso en contra de la gravedad. Esto se llama acción capilar y ocurre porque el agua se adhiere a las paredes del vidrio y la tensión superficial la jala hacia arriba. Si el líquido no se adhiere al tubo (como el mercurio en vidrio), el nivel del líquido bajará en el tubo.
Charcos en superficies
Cuando viertes mercurio sobre una superficie plana de vidrio, forma un charco que tiene un grosor notable y no se extiende mucho. Esto es porque la fuerte tensión superficial del mercurio lo hace contraerse y mantener una forma más compacta. Si viertes agua sobre una superficie encerada (a la que el agua no se pega bien), verás un efecto similar.
Gotas de agua de mar
La tensión superficial del agua de mar es un poco diferente a la del agua dulce debido a la salinidad. Los científicos han desarrollado ecuaciones para calcular la tensión superficial del agua de mar en diferentes temperaturas y niveles de sal.
Datos de tensión superficial de algunos líquidos
Aquí tienes algunos ejemplos de tensión superficial de diferentes líquidos a 20°C (a menos que se indique lo contrario), medida en dinas por centímetro (dyn/cm), que es lo mismo que milinewtons por metro (mN/m):
| Líquido | Temperatura (°C) | Tensión Superficial 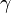 |
|---|---|---|
| Ácido acético | 20 | 27.60 |
| Acetona | 20 | 23.70 |
| Sangre | 22 | 55.89 |
| Etanol | 20 | 22.27 |
| Glicerol | 20 | 63.00 |
| Hexano | 20 | 18.40 |
| Mercurio | 15 | 487.00 |
| Metanol | 20 | 22.60 |
| Agua | 0 | 75.64 |
| Agua | 25 | 71.97 |
| Agua | 50 | 67.91 |
| Agua | 100 | 58.85 |
Galería de imágenes
Véase también
 En inglés: Surface tension Facts for Kids
En inglés: Surface tension Facts for Kids