Matemática aplicada para niños
La matemática aplicada es una rama de las matemáticas que se enfoca en usar herramientas y métodos matemáticos para resolver problemas en el mundo real. Estos problemas pueden venir de áreas como la ciencia, la ingeniería, la medicina o la economía.
Imagina que quieres diseñar un avión, predecir el clima o crear un videojuego en 3D. Para todo esto, los matemáticos aplicados usan conceptos como el cálculo, el álgebra lineal y las ecuaciones diferenciales. Su objetivo principal es llevar las matemáticas "hacia afuera", es decir, aplicarlas a otras áreas para encontrar soluciones prácticas.
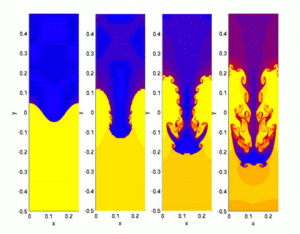
La matemática aplicada es muy útil para crear modelos, hacer simulaciones y mejorar procesos. Por ejemplo, se usa para simular cómo se comporta el aire alrededor de un transbordador espacial o para diseñar experimentos. También es fundamental para el desarrollo de simuladores y videojuegos modernos.
Contenido
Historia de la matemática aplicada
Históricamente, la matemática aplicada se centraba mucho en el análisis aplicado, especialmente en las ecuaciones diferenciales. También incluía la teoría de la aproximación y la probabilidad aplicada. Estas áreas estaban muy ligadas al desarrollo de la física newtoniana.
De hecho, durante mucho tiempo, no había una gran diferencia entre matemáticos y físicos. Materias como la mecánica clásica (que estudia el movimiento de los objetos) se enseñaban en los departamentos de matemáticas aplicadas. Hoy en día, los departamentos de ingeniería y ciencias de la computación también usan mucho la matemática aplicada.
Ramas de la matemática aplicada
Hoy en día, el término "matemática aplicada" es mucho más amplio. Incluye las áreas clásicas y muchas otras que se han vuelto importantes. Incluso campos de la matemática pura, como la teoría de números, son ahora útiles en aplicaciones como la criptografía (que se usa para proteger información).
No hay una lista única de todas las ramas de la matemática aplicada. Esto se debe a que las matemáticas y la ciencia cambian constantemente. Además, cada universidad organiza sus departamentos y cursos de manera diferente.
Algunos matemáticos distinguen entre "matemática aplicada" (que crea métodos matemáticos) y "aplicaciones de la matemática" (que usan esos métodos en otras ciencias). Por ejemplo, un biólogo que usa un modelo matemático para estudiar poblaciones de animales estaría "usando" las matemáticas, no necesariamente "haciendo" matemática aplicada. Sin embargo, los problemas de los biólogos pueden inspirar nuevas ideas en las matemáticas.
El éxito de los métodos matemáticos modernos y el software ha dado lugar a campos como la matemática computacional. Estos campos usan supercomputadoras para simular fenómenos y resolver problemas complejos en ciencia e ingeniería.
Matemáticas aplicables
A veces se usa el término "matemáticas aplicables" para diferenciar las matemáticas aplicadas tradicionales de las nuevas áreas de las matemáticas que se pueden usar en problemas del mundo real. No hay una definición exacta, pero la idea es que muchas áreas de las matemáticas, incluso las que antes se consideraban "puras", ahora tienen aplicaciones.
Por ejemplo, la criptografía usa la teoría de números, que es una parte de las matemáticas puras. Las "matemáticas aplicables" pueden verse como un conjunto de herramientas matemáticas como el análisis real, el álgebra lineal, la modelización matemática, la optimización, la combinatoria, la probabilidad y la estadística. Todas estas son útiles en muchas áreas fuera de las matemáticas tradicionales.
Utilidad de la matemática aplicada
Históricamente, las matemáticas han sido muy importantes en las ciencias naturales y la ingeniería. Pero desde la Segunda Guerra Mundial, otras áreas han impulsado nuevas ramas de las matemáticas. Por ejemplo, la teoría de los juegos y la teoría de la elección social surgieron de ideas económicas.
El uso de métodos matemáticos se ha extendido a muchos campos. Esto ha llevado a la creación de nuevas áreas como las finanzas matemáticas y la ciencia de los datos.
La llegada de las computadoras ha permitido nuevas aplicaciones. Ahora se puede estudiar y usar la tecnología informática para resolver problemas en otras ciencias (ciencia computacional). También se estudian las matemáticas de la computación, como el análisis numérico. La estadística es una disciplina matemática muy usada en las ciencias sociales.
Matemáticas básicas frente a matemáticas aplicadas
Los matemáticos siempre han tenido diferentes opiniones sobre la diferencia entre las matemáticas puras (o básicas) y las aplicadas. Un ejemplo famoso es el del matemático G.H. Hardy.
Hardy prefería las matemáticas básicas, que comparaba con la pintura y la poesía. Él pensaba que la diferencia era que las matemáticas aplicadas buscan expresar verdades "físicas" usando las matemáticas. En cambio, las matemáticas básicas expresan verdades que no dependen del mundo físico. Hardy distinguía entre matemáticas "reales" (con valor estético) y las partes "aburridas y elementales" que tienen un uso práctico.
Hardy consideraba que algunos físicos, como Albert Einstein y Paul Dirac, eran matemáticos "reales". En su momento, pensaba que la relatividad general y la mecánica cuántica eran "inútiles". Esto le permitía creer que solo las matemáticas "aburridas" eran útiles. Sin embargo, admitió que, al igual que la teoría de matrices y la teoría de grupos se aplicaron inesperadamente a la física, algún día las matemáticas "reales" y bellas también podrían ser útiles.
Otro punto de vista interesante es que las matemáticas aplicadas son un subconjunto de las matemáticas en general. Es decir, todas las matemáticas pueden ser aplicadas, pero algunas no lo son necesariamente.
También se ha argumentado que los conceptos matemáticos, como los números y las figuras, no fueron inventados de la nada. Surgieron de la observación del mundo real y de las necesidades de las personas. Aunque las leyes matemáticas se abstraen del mundo real, en cierto punto se vuelven independientes y se usan para entenderlo.
Áreas de las matemáticas con aplicaciones frecuentes
Cálculo diferencial e integral
El cálculo diferencial e integral se usa en casi todas las ramas de las ciencias naturales, la estadística, la ingeniería y la economía. También se aplica en los negocios, la medicina y la demografía. Es útil en cualquier área donde un problema se pueda representar con variables continuas y se busque una solución óptima. También sirve para entender ciclos e interacciones entre variables.
Como dijo Steven Strogatz: "El interior de un átomo, las poblaciones cambiantes de la vida salvaje, el clima… todo eso puede explicarse mediante el lenguaje del cálculo. De alguna manera este lenguaje… es simplemente la mejor herramienta que jamás hayamos inventado".
Análisis numérico
El análisis numérico tiene muchas subdisciplinas. Algunas de las principales son:
- Interpolación, extrapolación y regresión
- La interpolación ayuda a encontrar el valor de una función desconocida entre puntos de datos que ya conocemos.
- La extrapolación es similar, pero busca el valor de la función fuera de los puntos de datos conocidos.
- La regresión también es parecida, pero considera que los datos pueden tener errores. Ayuda a encontrar la función desconocida a partir de puntos de datos con mediciones imprecisas. Un método común es el de los mínimos cuadrados.
- Resolución de ecuaciones y sistemas de ecuaciones
Otro problema importante es encontrar la solución de una ecuación. Se distinguen dos casos: ecuaciones lineales y no lineales.
Se ha trabajado mucho en métodos para resolver sistemas de ecuaciones lineales. Los métodos directos incluyen la eliminación gaussiana. Los métodos iterativos, como el método de Jacobi, son preferidos para sistemas muy grandes.
Los algoritmos de búsqueda de raíces se usan para resolver ecuaciones no lineales. Si se conoce la derivada de la función, el método de Newton es una opción popular.
- Resolución de problemas de valores propios o de valores singulares
Muchos problemas importantes se pueden expresar usando la descomposición de valores propios o la descomposición de valores singulares. Por ejemplo, la compresión de imágenes se basa en la descomposición de valores singulares. En estadística, la herramienta similar se llama análisis de componentes principales.
- Optimización
Los problemas de optimización buscan el punto donde una función alcanza su valor máximo o mínimo. A menudo, este punto debe cumplir ciertas condiciones.
La optimización se divide en subcampos según la forma de la función y las restricciones. Por ejemplo, la programación lineal trata casos donde la función y las restricciones son lineales. Un método famoso es el método simplex.
Los multiplicadores de Lagrange pueden usarse para simplificar problemas de optimización con restricciones.
- Evaluación de integrales
La integración numérica, también conocida como cuadratura numérica, busca el valor de una integral definida. Métodos populares usan las fórmulas de Newton-Cotes (como la regla del punto medio) o la cuadratura gaussiana. Estos métodos dividen una integral grande en integrales más pequeñas. En dimensiones altas, donde estos métodos son muy costosos, se puede usar el método de Montecarlo.
- Ecuaciones diferenciales
El análisis numérico también se encarga de calcular soluciones aproximadas para las ecuaciones diferenciales, tanto las ordinarias como las ecuaciones en derivadas parciales.
Las ecuaciones diferenciales parciales se resuelven dividiendo la ecuación en partes más pequeñas. Esto se puede hacer con el método de elementos finitos o el método de diferencias finitas.
- Álgebra lineal
- Análisis complejo
- Análisis funcional
- Ecuaciones diferenciales
- Estadística inferencial
- Investigación operativa
- Matemática discreta
- Optimización
- Sistemas dinámicos
- Teoría de control
- Cálculo de probabilidad
- Fractales
El análisis numérico y la computación científica son partes centrales de las matemáticas aplicadas.
Galería de imágenes
-
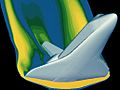
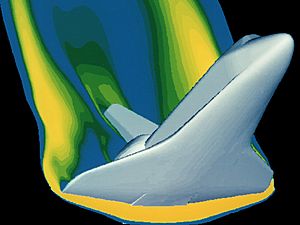
Una simulación por computador de un flujo de aire de alta velocidad alrededor de un transbordador espacial durante la reentrada. Este tipo de simulaciones requieren de complejos y poderosos métodos de matemática aplicada e ingeniería mecánica.
-
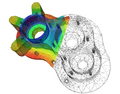
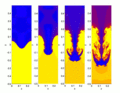
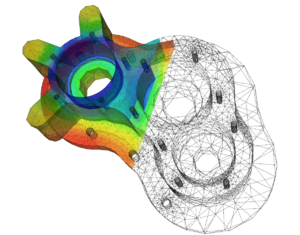
Una solución numérica de la ecuación del calor en un modelo de carcasa de bomba utilizando el método de elementos finitos.
-
La mecánica de fluidos suele considerarse una rama de la matemática aplicadas y de la ingeniería mecánica
-
En el ámbito de las finanzas se aplican las matemáticas para modelar y analizar el comportamiento de los mercados financieros
-
Tanto la mecánica clásica como la mecánica relativista utilizan el lenguaje del cálculo. Esto a su vez permite entender el movimiento de cuerpos celestes y realizar viajes espaciales o poner en órbita satélites artificiales
Véase también
En inglés: Applied mathematics Facts for Kids
