Teoría de la probabilidad para niños
La teoría de la probabilidad es una parte de las matemáticas que estudia los eventos que ocurren al azar. Imagina que lanzas un dado o una moneda: no puedes saber con seguridad qué resultado obtendrás, ¿verdad? Esos son eventos aleatorios.
A diferencia de los eventos aleatorios, existen los eventos deterministas. Estos son aquellos que siempre dan el mismo resultado si los haces bajo las mismas condiciones. Por ejemplo, si calientas agua a 100 grados Celsius al nivel del mar, siempre se convertirá en vapor. La teoría de la probabilidad nos ayuda a entender y medir la posibilidad de que ocurran los eventos aleatorios. Nos permite saber si un suceso es más probable que otro.
Muchos fenómenos en la naturaleza son aleatorios. La teoría de la probabilidad es muy útil para entenderlos, incluso si no conocemos todos los detalles.
En 1933, un matemático llamado Andréi Kolmogórov creó un sistema de reglas para la teoría de la probabilidad. Esto ayudó a que esta rama de las matemáticas fuera más precisa y se pudiera aplicar a muchos más problemas. Hoy en día, la teoría de la probabilidad se usa en muchas áreas, como la física (para entender el movimiento de partículas muy pequeñas, como el movimiento Browniano) y la economía (para analizar mercados).
Como base de la estadística, la teoría de la probabilidad es clave para analizar datos en muchas actividades humanas. También se usa para describir sistemas complejos cuando solo conocemos una parte de su estado. Un gran descubrimiento en la física del siglo XX fue que los fenómenos a nivel atómico son probabilísticos, algo que se describe en la mecánica cuántica.
Contenido
¿Qué es la probabilidad?
Origen de la probabilidad
La teoría de la probabilidad comenzó a desarrollarse gracias a preguntas que surgieron de los juegos de azar. Al principio, no había una teoría muy formal. La idea principal era calcular la probabilidad como una relación entre cuántas veces podía ocurrir un evento favorable y el número total de resultados posibles.
Por ejemplo, si lanzas una moneda, hay dos resultados posibles: cara o cruz. Si quieres saber la probabilidad de que salga cara, hay 1 caso favorable (cara) y 2 casos posibles (cara o cruz). Así, la probabilidad es 1/2.
Matemáticos como Gerolamo Cardano en el siglo XVI, y Pierre de Fermat y Blaise Pascal en el siglo XVII, fueron pioneros en estudiar estos problemas. Más tarde, en el siglo XIX, Pierre-Simon Laplace completó lo que se conoce como la definición clásica de probabilidad.
La forma moderna y más completa de definir la probabilidad fue propuesta por Andréi Kolmogórov. Su trabajo hizo que la probabilidad se convirtiera en una rama matemática muy sólida.
La probabilidad clásica: casos favorables entre casos posibles
La probabilidad de que un evento suceda es una medida de cuán posible es que ocurra. Se calcula dividiendo el número de veces que el evento puede ocurrir (casos favorables) entre el número total de resultados posibles, siempre que todos los resultados sean igual de probables.
Por ejemplo, si lanzas un dado de seis caras, ¿cuál es la probabilidad de que salga un número par? Los números pares son 2, 4 y 6 (3 casos favorables). El total de resultados posibles es 1, 2, 3, 4, 5, 6 (6 casos posibles). Entonces, la probabilidad es 3/6, que es igual a 1/2.
La probabilidad siempre es un número entre 0 y 1.
- Si un evento es imposible, su probabilidad es 0.
- Si un evento es seguro y siempre va a ocurrir, su probabilidad es 1.
Si p es la probabilidad de que un evento ocurra, y q es la probabilidad de que no ocurra, entonces siempre se cumple que p + q = 1.
La probabilidad moderna: un enfoque más amplio
La definición moderna de probabilidad es más avanzada y permite estudiar situaciones más complejas. Se basa en la idea de un "espacio muestral", que es el conjunto de todos los resultados posibles de un experimento.
Para cada resultado posible, se le asigna un valor de "probabilidad" que cumple dos reglas importantes:
- El valor de probabilidad de cada resultado debe estar entre 0 y 1.
- La suma de las probabilidades de todos los resultados posibles debe ser igual a 1.
Así, la probabilidad de un evento (que es un grupo de resultados) se calcula sumando las probabilidades de cada resultado que forma parte de ese evento.
Tipos de probabilidad
La teoría de la probabilidad se puede dividir en dos grandes tipos, dependiendo de los resultados que se estudian:
Probabilidad discreta
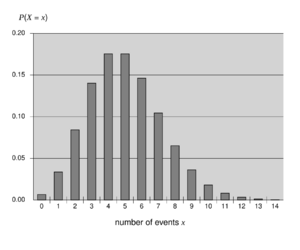
La probabilidad discreta se ocupa de eventos donde los resultados son contables. Esto significa que puedes enumerar todos los resultados posibles, incluso si son muchos.
Ejemplos de probabilidad discreta son:
En estos casos, los resultados son números enteros o categorías específicas.
Probabilidad continua
La probabilidad continua se usa cuando los resultados pueden tomar cualquier valor dentro de un rango. Por ejemplo, la altura de una persona, el tiempo que tardas en llegar a la escuela o la temperatura. Estos valores no se pueden contar uno por uno, ya que hay infinitas posibilidades entre dos puntos.
Variables aleatorias
Una variable aleatoria es una forma de asignar un número a cada resultado posible de un experimento aleatorio. Esto nos ayuda a trabajar con los resultados de manera matemática.
Por ejemplo, al lanzar una moneda, los resultados son "cara" y "cruz". Podemos definir una variable aleatoria X que asigne el número 0 a "cara" y el número 1 a "cruz". Así, en lugar de trabajar con palabras, trabajamos con números.
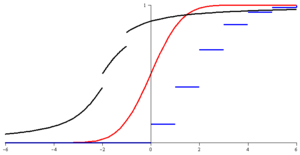
Función de distribución de probabilidad
La función de distribución de probabilidad nos dice la probabilidad de que una variable aleatoria tome un valor igual o menor que un número específico. Es como una tabla o un gráfico que muestra cómo se distribuyen las probabilidades de los diferentes resultados.
Función de densidad de probabilidad
Para las variables aleatorias continuas, usamos la función de densidad de probabilidad. Esta función nos ayuda a calcular la probabilidad de que un resultado caiga dentro de un cierto rango de valores.
Áreas de estudio en la teoría de la probabilidad
La teoría de la probabilidad moderna abarca muchos temas importantes, como:
- El estudio de las variables aleatorias y cómo se distribuyen sus probabilidades.
- La independencia probabilística, que nos dice si un evento afecta la probabilidad de otro.
- La Probabilidad condicionada, que es la probabilidad de que un evento ocurra sabiendo que otro ya ocurrió.
- Las Leyes de los grandes números, que explican cómo los promedios de muchos eventos aleatorios tienden a acercarse a un valor esperado.
- El Teorema central del límite, que es muy importante para la estadística y nos dice que la suma de muchas variables aleatorias tiende a seguir una distribución específica.
- Los procesos estocásticos, que son series de eventos aleatorios que cambian con el tiempo.
Véase también
 En inglés: Probability theory Facts for Kids
En inglés: Probability theory Facts for Kids