Programación lineal para niños
La programación lineal es una herramienta matemática que nos ayuda a encontrar la mejor manera de hacer algo. Imagina que tienes un objetivo, como ganar la mayor cantidad de dinero o gastar lo menos posible. La programación lineal te ayuda a lograr ese objetivo, pero siempre teniendo en cuenta ciertas reglas o límites que debes seguir.
Estas reglas se llaman "restricciones" y se escriben como ecuaciones o desigualdades matemáticas. Las cosas que puedes cambiar para alcanzar tu objetivo se llaman "variables". El método más conocido para resolver estos problemas es el Método Simplex.
Contenido
¿Qué es la Programación Lineal?
La programación lineal es una parte de las matemáticas que se usa para optimizar (es decir, maximizar o minimizar) una función. Esta función se llama "función objetivo" y representa lo que quieres lograr, como el beneficio de una empresa o el costo de un proyecto.
Para encontrar la mejor solución, las "variables" de esta función (que son los elementos que puedes ajustar) deben cumplir con una serie de "restricciones". Estas restricciones son como reglas o límites que se expresan con ecuaciones o desigualdades lineales. Por ejemplo, si estás fabricando juguetes, una restricción podría ser que no puedes usar más de cierta cantidad de plástico al día.
La zona donde todas las restricciones se cumplen se llama "región factible". La programación lineal busca el punto dentro de esa región que te da el mejor resultado para tu función objetivo.
Un Poco de Historia
La idea de resolver sistemas de desigualdades lineales se remonta al menos a Joseph Fourier en 1826. Sin embargo, la programación lineal como la conocemos hoy se desarrolló durante la Segunda Guerra Mundial. Se usó para planificar cómo usar los recursos de manera eficiente y reducir gastos. Al principio, esta técnica se mantuvo en secreto.
Después de la guerra, muchas industrias comenzaron a usarla en su día a día. Los principales creadores de esta técnica son:
- George Dantzig, quien publicó el algoritmo simplex en 1947.
- John von Neumann, que desarrolló una teoría importante llamada "teoría de la dualidad" en el mismo año.
- Leonid Kantoróvich, un matemático ruso que también trabajó en ideas similares antes que Dantzig y ganó un premio Nobel en economía en 1975.
En 1979, otro matemático ruso, Leonid Khachiyan, creó el Algoritmo del elipsoide, que demostró que estos problemas se pueden resolver de forma eficiente. Más tarde, en 1984, Narendra Karmarkar introdujo un nuevo método que mejoró mucho la forma de resolver estos problemas.
Un ejemplo famoso de la utilidad de la programación lineal es el de Dantzig, que buscaba la mejor manera de asignar 70 personas a 70 trabajos. Si intentaras probar todas las combinaciones posibles, ¡sería un número gigantesco, más grande que el número de partículas en el universo! Pero con la programación lineal y el algoritmo simplex, encontrar la mejor solución toma muy poco tiempo. Esta teoría reduce drásticamente la cantidad de soluciones que hay que revisar.
| Año | Acontecimiento |
|---|---|
| 1826 | Joseph Fourier trabaja con ideas relacionadas. |
| 1902 | Gyula Farkas crea un método para resolver sistemas de desigualdades. |
| 1947 | George Dantzig publica el algoritmo simplex y John von Neumann desarrolla la teoría de la dualidad. |
| 1984 | Narendra Karmarkar introduce el método del punto interior. |
¿Para qué sirve la Programación Lineal?
La programación lineal es muy útil en muchos campos. Ayuda a tomar decisiones inteligentes en situaciones donde hay recursos limitados o reglas que seguir.
Algunos ejemplos de cómo se usa son:
- Mezcla de alimentos: Para crear la receta más barata que cumpla con ciertos requisitos nutricionales.
- Gestión de inventarios: Decidir cuánto producto almacenar para satisfacer la demanda sin gastar demasiado.
- Asignación de recursos: Distribuir personas o máquinas a diferentes tareas para ser lo más eficientes posible.
- Planificación de publicidad: Decidir dónde y cuándo poner anuncios para llegar a la mayor cantidad de gente con el menor costo.
- Economía y negocios: Ayuda a las empresas a maximizar sus ganancias o minimizar sus costos de producción.
- Ingeniería: Por ejemplo, para optimizar cómo se distribuye el agua en una red o cómo se usan los recursos de una cuenca de río.
- Problemas de transporte: Encontrar la ruta más barata para llevar productos de un lugar a otro.
Aprender sobre programación lineal es importante porque nos da herramientas para mejorar la toma de decisiones en muchos aspectos de la vida y los negocios.
Un Ejemplo Práctico
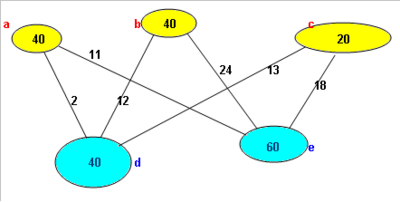
Imagina que tenemos tres minas de carbón y dos centrales eléctricas que necesitan carbón. Queremos saber cómo transportar el carbón de las minas a las centrales de la forma más barata posible.
- Producción de las minas por día:
* Mina "a": 40 toneladas * Mina "b": 40 toneladas * Mina "c": 20 toneladas
- Consumo de las centrales por día:
* Central "d": 40 toneladas * Central "e": 60 toneladas
- Costos de transporte por tonelada:
* De "a" a "d": 2 monedas * De "a" a "e": 11 monedas * De "b" a "d": 12 monedas * De "b" a "e": 24 monedas * De "c" a "d": 13 monedas * De "c" a "e": 18 monedas
Si solo nos fijamos en el costo más bajo (de "a" a "d" por 2 monedas), podríamos pensar que la mejor opción es enviar todo lo posible por ahí.
- Transporte de 40 t de "a" a "d" = 80 monedas
- Transporte de 20 t de "c" a "e" = 360 monedas (para cubrir lo que falta en "e")
- Transporte de 40 t de "b" a "e" = 960 monedas (para cubrir el resto de "e")
- Costo total: 1.400 monedas
Pero, si usamos la programación lineal, el problema se plantea con ecuaciones que representan las restricciones de producción y consumo, y una función objetivo que queremos minimizar (el costo total).
- Restricciones de producción:
* Lo que sale de la mina "a" (hacia "d" y "e") no puede ser más de 40 toneladas. * Lo que sale de la mina "b" (hacia "d" y "e") no puede ser más de 40 toneladas. * Lo que sale de la mina "c" (hacia "d" y "e") no puede ser más de 20 toneladas.
- Restricciones de consumo:
* Lo que llega a la central "d" (de "a", "b" y "c") debe ser al menos 40 toneladas. * Lo que llega a la central "e" (de "a", "b" y "c") debe ser al menos 60 toneladas.
- Función objetivo (lo que queremos minimizar):
* 2 * (toneladas de a a d) + 11 * (toneladas de a a e) + 12 * (toneladas de b a d) + 24 * (toneladas de b a e) + 13 * (toneladas de c a d) + 18 * (toneladas de c a e)
Al resolver este problema con programación lineal, la solución de costo mínimo es:
- Enviar 40 t de "b" a "d" = 12 x 40 = 480 monedas
- Enviar 40 t de "a" a "e" = 11 x 40 = 440 monedas
- Enviar 20 t de "c" a "e" = 18 x 20 = 360 monedas
- Costo total: 1.280 monedas
¡Esto es 120 monedas menos que la primera idea! Este ejemplo muestra cómo la programación lineal nos ayuda a encontrar la mejor solución, incluso cuando no es la más obvia a primera vista.
Galería de imágenes
Véase también
 En inglés: Linear programming Facts for Kids
En inglés: Linear programming Facts for Kids