Teoría de la aproximación para niños
En matemáticas, la teoría de la aproximación es el estudio de cómo podemos representar funciones complicadas usando otras funciones más sencillas. También nos ayuda a medir qué tan grande es el error cuando hacemos esa simplificación.
Lo que consideramos "mejor" o "más simple" depende de para qué queremos usar la aproximación. También influye la cantidad de cálculos que podemos hacer.
Un tema relacionado es usar series de Fourier generalizadas para aproximar funciones. Esto se hace sumando muchos términos basados en polinomios ortogonales.
Contenido
¿Por qué es importante la aproximación en las computadoras?
Un uso muy importante de la teoría de la aproximación es en las computadoras. Las computadoras necesitan calcular funciones complejas, como el logaritmo o la exponencial. Sin embargo, solo pueden hacer operaciones básicas como sumar y multiplicar.
Para resolver esto, se usan funciones más simples, como los polinomios o las funciones racionales. Estas son divisiones de polinomios. El objetivo es que el resultado sea lo más parecido posible a la función original.
Para lograr una gran precisión, se pueden usar polinomios de un grado alto. Otra forma es reducir el rango de números donde el polinomio debe funcionar.
A menudo, se divide el rango de números en partes más pequeñas. Luego, se usa un polinomio más sencillo para cada parte. Así, se mantiene la precisión sin usar polinomios demasiado complejos.
¿Cómo surgió la idea de la aproximación?
La necesidad de aproximar funciones apareció muy temprano en la geometría. Por ejemplo, con las funciones trigonométricas (como seno o coseno). Conocemos sus propiedades, pero no se pueden calcular fácilmente con operaciones básicas.
Esto llevó a la idea de "desarrollar" funciones en series. Así nacieron las tablas trigonométricas. Luego, se crearon tablas para logaritmos y otras funciones comunes en la ciencia, como la raíz cuadrada.
El objetivo es que la aproximación sea lo más precisa posible. Esto significa que los valores calculados deben ser muy cercanos a los valores reales. Se busca una precisión similar a la que usan las computadoras.
Una vez que se elige el rango de números y el tipo de polinomio, se busca el polinomio que minimice el error. Es decir, queremos que la diferencia entre la función real y el polinomio sea lo más pequeña posible.
Para una función "normal", el mejor polinomio de un cierto grado tiene una característica especial. El error entre el polinomio y la función real cambia de signo varias veces. Esto asegura que el error máximo sea el menor posible.
Polinomios Óptimos: ¿Cuál es la mejor aproximación?
Cuando elegimos un rango de números y el grado de un polinomio, buscamos el polinomio que tenga el menor error posible. Esto significa que queremos que la diferencia máxima entre el polinomio que usamos (P(x)) y la función real (f(x)) sea lo más pequeña posible.
Para funciones que se comportan bien, existe un polinomio de grado N. Este polinomio hace que la curva de error oscile entre un valor positivo (+ε) y un valor negativo (-ε) un total de N+2 veces. Esto nos da el límite del peor error posible, que es ε.
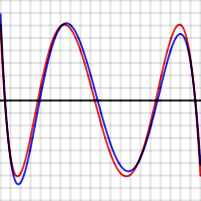
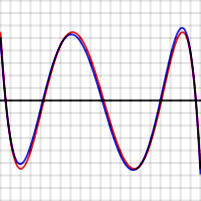
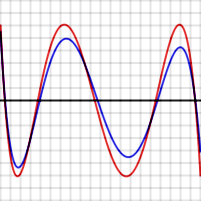
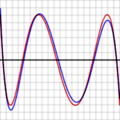
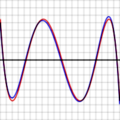
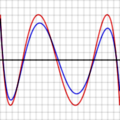
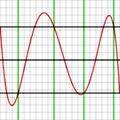
Por ejemplo, mira los gráficos de la derecha. Muestran el error al aproximar log(x) y exp(x) con un polinomio de grado 4. Las líneas rojas representan el polinomio óptimo. Estas líneas oscilan exactamente entre +ε y -ε. Observa que en cada caso, hay N+2 (es decir, 6) puntos donde el error alcanza su valor máximo o mínimo. Dos de estos puntos están en los extremos del rango.
Para entender por qué este polinomio es el mejor, imagina que hay otro polinomio que es "mejor". Si restamos el error de este supuesto "mejor" polinomio al error del polinomio óptimo, obtenemos un nuevo polinomio. Este nuevo polinomio tendría que cambiar de signo más veces de lo que es posible para su grado. Esto demuestra que el polinomio óptimo es realmente el mejor.
Aproximación de Chebyshev: Una forma práctica de aproximar
Podemos obtener polinomios muy cercanos a los óptimos usando los polinomios de Chebyshov. Para ello, "expandimos" la función que queremos aproximar usando estos polinomios. Luego, simplemente cortamos la expansión en el grado que deseamos.
Este método es parecido al análisis de Fourier. Pero en lugar de usar funciones trigonométricas, usamos los polinomios de Chebyshev.
Si calculamos los coeficientes de la expansión de Chebyshev para una función y luego cortamos la serie, obtenemos un polinomio que se acerca a la función original.
La razón por la que este polinomio es casi el mejor es que el error que queda después de cortar la serie es muy parecido a un múltiplo del siguiente polinomio de Chebyshev. Los polinomios de Chebyshev tienen la propiedad de que sus valores oscilan entre +1 y -1. Esto significa que el error de la aproximación de Chebyshev se parece mucho al error del polinomio óptimo.
En los gráficos de arriba, la línea de error azul (aproximación de Chebyshev) a veces es mejor que la roja (óptima), y a veces es peor. Esto significa que no es el polinomio óptimo, pero está muy cerca. La diferencia es menor para la función exponencial, que tiene una serie que converge muy rápido.
Algoritmo de Remez: Encontrando el polinomio perfecto
El algoritmo Remez (a veces llamado Remes) se usa para encontrar el polinomio óptimo. Este polinomio se acerca a una función dada en un rango específico. Es un proceso que se repite varias veces. Al final, el algoritmo encuentra un polinomio cuyo error tiene N+2 puntos donde alcanza sus valores máximos o mínimos, alternando entre positivo y negativo. Según lo que vimos antes, este polinomio es el mejor.
El algoritmo de Remez funciona así: 1. Se eligen N+2 puntos de partida. 2. Se resuelven unas ecuaciones para encontrar un polinomio y un valor de error (ε). 3. Se observa dónde están los errores máximos y mínimos reales de este polinomio. 4. Se mueven los puntos de partida a esas nuevas ubicaciones. 5. Se repiten los pasos 2 a 4 hasta que el resultado sea muy preciso.
Este algoritmo es muy rápido. Si los puntos de partida están cerca del resultado correcto, la precisión mejora muchísimo en cada paso.
Para empezar el algoritmo de Remez, a menudo se usan los puntos donde los polinomios de Chebyshev alcanzan sus valores extremos. Esto se debe a que el error final será similar a esos polinomios.
Galería de imágenes
-
Error entre el polinomio óptimo y log(x) (rojo), y la aproximación de Chebyshev y log(x) (azul) en el intervalo [2, 4]. Las divisiones verticales son de 10−5. El error máximo para el polinomio óptimo es de 6.07 × 10−5
-
Error entre el polinomio óptimo y exp(x) (rojo), y la aproximación de Chebyshev y exp(x) (azul) durante el intervalo [−1, 1]. Las divisiones verticales son de 10−4. El error máximo para el polinomio óptimo es 5.47 × 10−4
-
Error P(x) − f(x) para el polinomio de nivel (rojo), y para el supuesto mejor polinomio (azul).
-
Error del polinomio producido por el primer paso del algoritmo de Remez, aproximando ex en el intervalo [−1, 1]. Las divisiones verticales son de 10−4
Véase también
En inglés: Approximation theory Facts for Kids
- Polinomios de Chebyshov
- Estimación estadística
- Series de Fourier generalizadas
- Polinomios ortogonales
- Base ortonormal
- Serie de Fourier
- Base de Schauder
- Aproximante de Padé
- Función de aproximación
