Electromagnetismo para niños
El electromagnetismo es una parte de la física que estudia cómo la electricidad y el magnetismo están conectados. Imagina que son como dos caras de una misma moneda. Esta rama de la ciencia nos ayuda a entender cómo las partículas con carga eléctrica interactúan con los campos eléctricos y magnéticos. Es una de las fuerzas más importantes del universo.
El electromagnetismo explica muchos fenómenos que vemos a diario, como la luz. La luz es una especie de onda electromagnética que viaja por el espacio. La mayoría de las fuerzas que experimentamos, aparte de la gravedad, son resultado del electromagnetismo.
Los principios del electromagnetismo se usan en muchas áreas, como las microondas, las antenas, las máquinas eléctricas, las comunicaciones por satélite, la fibra óptica y la meteorología con radar. También se encuentran en dispositivos como transformadores, relés, radios, televisores, teléfonos, motores eléctricos y láseres.
Los científicos Michael Faraday y James Clerk Maxwell fueron clave en el desarrollo de la teoría del electromagnetismo. Maxwell, en 1865, formuló un conjunto de ecuaciones que describen cómo se relacionan los campos eléctricos y magnéticos. Esto fue un gran avance en la física.
El estudio de los campos electromagnéticos se divide en:
- Electrostática: que estudia las interacciones entre cargas eléctricas que están quietas.
- Electrodinámica: que estudia las interacciones entre cargas eléctricas que se mueven y la radiación.
El electromagnetismo es una teoría que usa conceptos como campos para explicar cómo las cargas eléctricas, tanto quietas como en movimiento, afectan a diferentes materiales.

Contenido
Descubriendo el Electromagnetismo

La historia del electromagnetismo se remonta a más de dos mil años. Desde la antigüedad, la gente conocía los efectos de la electricidad en la atmósfera, como los rayos y el fuego de San Telmo. Sin embargo, no entendían bien cómo funcionaban.
Durante los siglos XVII y XVIII, científicos como William Gilbert, Otto von Guericke, Stephen Gray, Benjamin Franklin y Alessandro Volta investigaron la electricidad y el magnetismo por separado, obteniendo resultados importantes.
A principios del siglo XIX, Hans Christian Ørsted descubrió que los fenómenos magnéticos y eléctricos estaban relacionados. A partir de ahí, el trabajo de físicos como André-Marie Ampère, William Sturgeon, Joseph Henry, Georg Simon Ohm y Michael Faraday fue unificado por James Clerk Maxwell en 1861. Maxwell creó un conjunto de ecuaciones que describían ambos fenómenos como uno solo: el electromagnetismo.
Las ecuaciones de Maxwell mostraron que los campos eléctricos y magnéticos eran parte de un único campo electromagnético. Además, explicaron que la luz es una onda electromagnética. Gracias a esta teoría, los científicos pudieron hacer grandes inventos, como la bombilla eléctrica de Thomas Alva Edison y el generador de corriente alterna de Nikola Tesla. El éxito de la teoría de Maxwell también llevó a Albert Einstein a desarrollar su teoría de la relatividad.
En la primera mitad del siglo XX, con el surgimiento de la mecánica cuántica, el electromagnetismo se adaptó a esta nueva teoría, dando lugar a la electrodinámica cuántica en la década de 1940.
¿Cómo se unieron la electricidad y el magnetismo?
Al principio, la electricidad y el magnetismo se veían como cosas separadas. Pero esto cambió con el trabajo de James Clerk Maxwell en 1873. Él demostró que la interacción entre cargas eléctricas positivas y negativas es parte de una misma fuerza.
Hay cuatro efectos principales que se han demostrado con experimentos:
- Las cargas eléctricas se atraen o se repelen. Las cargas diferentes se atraen (como un imán que atrae metal), y las cargas iguales se repelen (como dos imanes que se empujan). La fuerza disminuye si las cargas están más lejos.
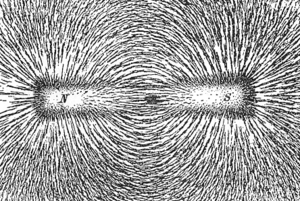
- Los polos magnéticos (norte y sur) también se atraen o se repelen de forma similar. Un polo norte siempre va con un polo sur; no existen solos.
- Una corriente eléctrica en un cable crea un campo magnético alrededor del cable. La dirección de este campo depende de cómo fluye la corriente.
- Se puede crear una corriente eléctrica en un cable si se mueve cerca de un campo magnético, o si un imán se mueve cerca del cable. La dirección de la corriente depende de cómo se muevan.
En 1820, el científico Hans Christian Ørsted hizo un descubrimiento sorprendente. Notó que la aguja de una brújula se movía cuando encendía o apagaba una corriente eléctrica cerca. Esto le hizo pensar que la electricidad y el magnetismo estaban conectados.
Ørsted no pudo explicarlo con fórmulas al principio, pero siguió investigando. Poco después, publicó sus resultados, mostrando que una corriente eléctrica crea un campo magnético. En honor a su trabajo, una unidad de medida para la inducción electromagnética se llama "Oersted".
El descubrimiento de Ørsted impulsó a muchos científicos a estudiar la relación entre electricidad y magnetismo. Dominique François Arago notó que un cable con corriente atraía limaduras de hierro y pudo magnetizar metales. También Michael Faraday hizo importantes descubrimientos.
Las ideas de Ørsted también influyeron en André-Marie Ampere, quien formuló leyes matemáticas para la interacción electromagnética.
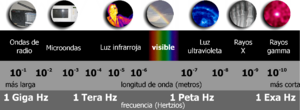
La unificación de estos conceptos, desarrollada por Michael Faraday, completada por James Clerk Maxwell, y mejorada por Oliver Heaviside y Heinrich Hertz, fue uno de los mayores logros del siglo XIX en la física. Este descubrimiento nos ayudó a entender la naturaleza de la luz. La luz y otras ondas electromagnéticas son como pequeñas "partículas" de energía llamadas fotones. Dependiendo de su frecuencia, estas ondas pueden ser ondas de radio, luz visible o incluso rayos gamma.
Ørsted no fue el único en notar esta conexión. En 1802, Giovanni Domenico Romagnosi, un jurista italiano, también desvió una aguja magnética con electricidad estática. Sin embargo, su descubrimiento no usaba corriente continua y no fue muy conocido en ese momento.
Ramas del Electromagnetismo
Electrostática: Cargas en Reposo
La electrostática estudia los fenómenos relacionados con los objetos que tienen carga eléctrica y están quietos. Estos objetos ejercen fuerzas entre sí, como se describe en la ley de Coulomb. Si las cargas son diferentes, se atraen; si son iguales, se repelen.
Podemos entender esto pensando en un campo eléctrico alrededor de cualquier objeto cargado. Si otro objeto cargado entra en este campo, sentirá una fuerza. La electrostática tiene muchas aplicaciones, desde entender las tormentas eléctricas hasta el funcionamiento de algunos tubos electrónicos.
La carga eléctrica es una propiedad fundamental de la materia. La carga más pequeña que conocemos es la del electrón. Un objeto tiene carga eléctrica si tiene demasiados o muy pocos electrones en sus átomos. Si le faltan electrones, tiene carga positiva; si le sobran, tiene carga negativa.
La unidad de carga eléctrica en el Sistema Internacional de Unidades es el culombio (C). Un culombio es la cantidad de carga que pasa en un segundo por un cable con una corriente de un amperio. Es una cantidad muy grande de electrones.
El movimiento de electrones por un material se llama corriente eléctrica. La cantidad de carga que pasa por unidad de tiempo es la intensidad de corriente. Otros conceptos importantes son la diferencia de potencial (o voltaje) y la resistencia eléctrica.
La ley de Coulomb, descubierta por Coulomb en 1785, describe la fuerza entre dos cargas eléctricas puntuales. Dice que la fuerza es más fuerte cuanto más cerca estén las cargas y cuanto mayores sean sus cargas.
Cuando tenemos muchas cargas, usamos el concepto de campo eléctrico. El campo eléctrico es una región del espacio donde actúan las fuerzas eléctricas. Nos permite saber la intensidad de la fuerza en cualquier punto sin necesidad de conocer todas las cargas que la provocan.
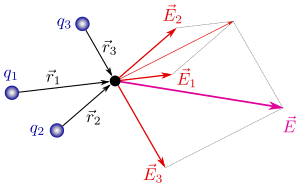
Otro concepto útil es el flujo eléctrico, que mide cuánta "fuerza" eléctrica atraviesa una superficie. El matemático Carl Friedrich Gauss demostró que el flujo eléctrico a través de una superficie cerrada es proporcional a la carga total dentro de esa superficie. Esto se conoce como la ley de Gauss.
Magnetostática: Magnetismo Constante
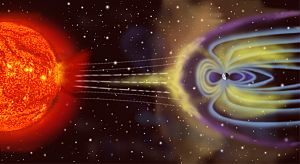
Antes de 1820, el magnetismo se estudiaba por separado. Pero cuando Hans Christian Ørsted descubrió la conexión con la electricidad, se empezó a desarrollar una teoría científica para el magnetismo. Una corriente eléctrica (cargas en movimiento) crea una fuerza magnética que no cambia con el tiempo.
Si una carga eléctrica se mueve en un campo magnético, sentirá una fuerza magnética. Esta fuerza depende de la velocidad de la carga y de la intensidad del campo magnético.
Jean Baptiste Biot y Félix Savart desarrollaron una ley, la ley de Biot-Savart, para calcular el campo magnético creado por corrientes eléctricas que no cambian. Esta ley nos ayuda a entender cómo se genera el magnetismo.
Se ha demostrado experimentalmente que las líneas de fuerza de los campos magnéticos siempre son cerradas, lo que significa que no existen "polos magnéticos" aislados (siempre hay un polo norte y un polo sur juntos). Esto se describe en la ley de Gauss para el campo magnético.
También existe la ley de Ampère, que es similar a la ley de Gauss para la electricidad. Esta ley nos dice que la "circulación" de un campo magnético alrededor de un camino cerrado es igual a la corriente eléctrica que pasa a través de la superficie encerrada por ese camino.
Electrodinámica Clásica: Cargas en Movimiento y Campos Variables
La electrodinámica estudia los fenómenos relacionados con las cargas eléctricas en movimiento y los campos eléctricos y magnéticos que cambian con el tiempo. Como una carga en movimiento produce un campo magnético, la electrodinámica abarca el magnetismo, la radiación electromagnética y la inducción electromagnética. Esto incluye aplicaciones prácticas como los generadores eléctricos y los motores eléctricos.
Esta área, conocida como electrodinámica clásica, fue explicada de forma completa por James Clerk Maxwell con sus famosas ecuaciones. Más recientemente, la electrodinámica cuántica combina las leyes de la teoría cuántica para explicar cómo la radiación electromagnética interactúa con la materia.
En las secciones anteriores, hablamos de campos eléctricos y magnéticos que no cambiaban. Pero a finales del siglo XIX, los físicos descubrieron que estos campos están conectados: un campo eléctrico que cambia (o una corriente eléctrica que varía) genera un campo magnético, y un campo magnético que cambia genera un campo eléctrico.
La fuerza que siente una partícula cargada que se mueve en un campo magnético y eléctrico se conoce como la fuerza de Lorentz. Esta fuerza combina los efectos eléctricos y magnéticos.
Michael Faraday descubrió que un campo magnético que cambia con el tiempo puede generar una corriente eléctrica en un circuito. Esto se llama inducción electromagnética y es la base de cómo funcionan los generadores.
James Clerk Maxwell unió todas estas ideas en sus cuatro ecuaciones, que son la base del electromagnetismo. Él también introdujo el concepto de "corriente de desplazamiento", que es clave para entender cómo los campos eléctricos que cambian pueden generar campos magnéticos.

La gran contribución de Maxwell fue que sus ecuaciones describen un campo electromagnético donde el campo eléctrico y el magnético están unidos, son perpendiculares entre sí y a la dirección en que se propagan. Estas ecuaciones predijeron la existencia de ondas que viajan a la velocidad de la luz, unificando así la electricidad, el magnetismo y la óptica.
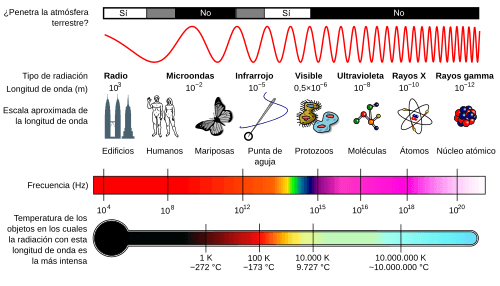
Esta onda electromagnética no necesita un medio para propagarse; puede viajar en el vacío gracias a la generación mutua de los campos magnéticos y eléctricos. Aunque su velocidad es constante (la velocidad de la luz), puede tener diferentes longitudes de onda y transportar energía. La radiación electromagnética recibe diferentes nombres según su longitud de onda, como rayos gamma, rayos X o espectro visible, y en conjunto forman el espectro electromagnético.
Electrodinámica Cuántica: El Nivel Más Pequeño
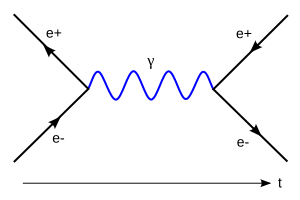
Después de la revolución de la mecánica cuántica a principios del siglo XX, los físicos buscaron una teoría cuántica para el electromagnetismo. El trabajo de Albert Einstein sobre el efecto fotoeléctrico sugirió que la interacción electromagnética ocurre mediante el intercambio de partículas llamadas fotones.
La electrodinámica cuántica (QED, por sus siglas en inglés) es una teoría que describe cómo interactúan los bosones (partículas que transmiten la fuerza, como los fotones) con otras partículas de materia (los fermiones). Fue desarrollada por científicos como Sinitiro Tomonaga, Julian Schwinger, Richard Feynman y Freeman Dyson entre 1947 y 1949.
En la electrodinámica cuántica, la interacción entre partículas se describe con un lenguaje matemático que incluye la idea de "simetría". El campo electromagnético se ve como estados de fotones que transmiten la interacción.
Unidades de Medida del Electromagnetismo en el SI
|
Unidades de electromagnetismo del SI Unidades de electromagnetismo del SI
|
|||||
|---|---|---|---|---|---|
|
Esta sección es un extracto de Unidades de electromagnetismo del SI.
Las Unidades de electromagnetismo del SI son las unidades usadas para medir fenómenos electromagnéticos dentro del Sistema Internacional de unidades. Solo la corriente eléctrica es una de las siete unidades básicas; las demás son unidades derivadas. {- |
Símbolo | Magnitud | Nombre de la unidad | Símbolo de la unidad | Fórmula de la unidad |
Véase también
 En inglés: Electromagnetism Facts for Kids
En inglés: Electromagnetism Facts for Kids