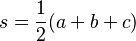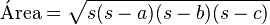Triángulo para niños
Datos para niños Triángulo |
||
|---|---|---|
 Varios tipos de triángulos
|
||
| Características | ||
| Lados | 3 | |
| Vértices | 3 | |
| Símbolo de Schläfli | {3} (para el triángulo equilátero) | |
| Área | varios métodos; véase artículo |
|
| Ángulo interior | 60° (para el triángulo equilátero) | |
En geometría, un triángulo es una figura plana que tiene tres lados rectos. También se le conoce como trígono. Los puntos donde se unen los lados se llaman vértices.
Un triángulo siempre tiene tres ángulos interiores, tres lados y tres vértices.
Contenido
- ¿Qué es un triángulo y dónde se encuentra?
- Partes principales de un triángulo
- Tipos de triángulos: ¿Cómo se clasifican?
- Triángulos iguales (Congruencia)
- Triángulos parecidos (Semejanza)
- Propiedades importantes de los triángulos
- Puntos especiales en un triángulo
- Cómo calcular lados y ángulos
- Elementos especiales de un triángulo
- Cómo calcular el área de un triángulo
- Triángulos en el espacio
- Historia del triángulo
- Más sobre triángulos
- Véase también
¿Qué es un triángulo y dónde se encuentra?
Si un triángulo está en una superficie plana, como una hoja de papel, se le llama simplemente triángulo o trígono. Si está en una superficie curva, como una esfera, se le llama triángulo esférico. Cuando se dibuja en mapas de la Tierra, se le conoce como triángulo geodésico.
Partes principales de un triángulo
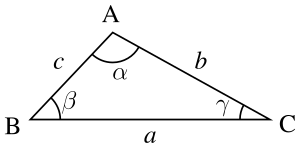
Vértices: Los puntos de unión
Los vértices son los puntos que forman un triángulo. Se suelen nombrar con letras mayúsculas, como A, B, C. Para que exista un triángulo, los tres puntos no deben estar en una misma línea recta.
Un triángulo se nombra usando sus vértices, por ejemplo, ABC. El orden de las letras no cambia el triángulo.
Lados: Las líneas que forman el triángulo
Cada par de vértices forma un segmento, que es un lado del triángulo. Los lados se nombran con las letras de sus vértices, como AB, BC y AC.
La longitud de un lado se suele representar con la letra minúscula del vértice opuesto. Por ejemplo, el lado opuesto al vértice A se llama a.
La suma de las longitudes de los tres lados de un triángulo se llama perímetro.
Ángulos: Las aberturas entre los lados
Un ángulo del triángulo es la abertura que se forma entre dos lados que se unen en un vértice. Se pueden nombrar con letras griegas como alfa (α), beta (β) y gamma (γ), o con la letra del vértice con un acento circunflejo, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \widehat{A} .
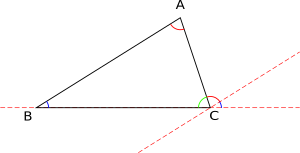
Un ángulo externo es el que se forma al prolongar uno de los lados del triángulo.
Tipos de triángulos: ¿Cómo se clasifican?
Los triángulos se pueden clasificar de dos maneras: por la longitud de sus lados o por la medida de sus ángulos.
Clasificación por la longitud de sus lados
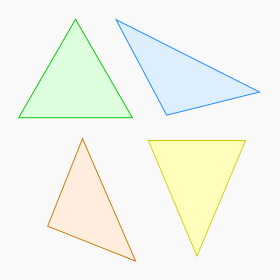
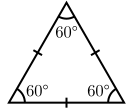
- Triángulo equilátero: Tiene sus tres lados de la misma longitud. Sus tres ángulos interiores también son iguales y miden 60 grados cada uno.
- Triángulo isósceles: Tiene al menos dos lados de la misma longitud. Los ángulos opuestos a esos lados iguales también tienen la misma medida. Un triángulo equilátero es un tipo especial de triángulo isósceles.
- Triángulo escaleno: Todos sus lados tienen longitudes diferentes. Por lo tanto, todos sus ángulos también son diferentes.
 |
 |
 |
|---|---|---|
| Equilátero | Isósceles | Escaleno |
Clasificación por la medida de sus ángulos
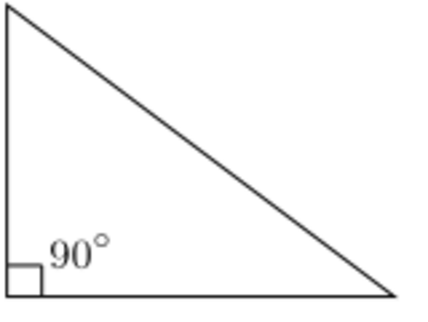
- Triángulo rectángulo: Tiene un ángulo interior que mide exactamente 90 grados (un ángulo recto). Los dos lados que forman el ángulo recto se llaman catetos, y el lado más largo, opuesto al ángulo recto, se llama hipotenusa.
- Triángulo oblicuángulo: Ninguno de sus ángulos interiores mide 90 grados. Los triángulos obtusángulos y acutángulos son oblicuángulos.
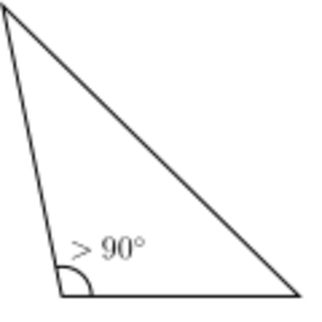
- Triángulo obtusángulo: Tiene un ángulo interior que mide más de 90 grados (un ángulo obtuso). Los otros dos ángulos son agudos (menores de 90 grados).
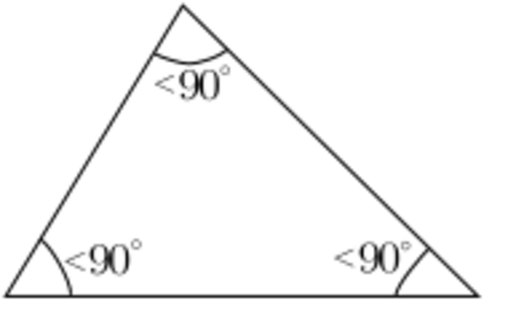
- Triángulo acutángulo: Sus tres ángulos interiores son agudos (todos miden menos de 90 grados).
-
Triángulo Rectángulo
-
Triángulo Obtusángulo
-
Triángulo Acutángulo
Combinando lados y ángulos
Los triángulos también se pueden clasificar combinando las dos formas anteriores:
- Acutángulo isósceles: Todos los ángulos son agudos, y dos lados son iguales.
- Acutángulo escaleno: Todos los ángulos son agudos y todos los lados son diferentes.
- Acutángulo equilátero: Sus tres lados y tres ángulos son iguales (todos 60 grados).
- Rectángulo isósceles: Tiene un ángulo recto y los dos catetos son iguales. Los otros dos ángulos miden 45 grados cada uno.
- Rectángulo escaleno: Tiene un ángulo recto y todos sus lados y ángulos son diferentes.
- Obtusángulo isósceles: Tiene un ángulo obtuso y los dos lados que forman ese ángulo son iguales.
- Obtusángulo escaleno: Tiene un ángulo obtuso y todos sus lados son diferentes.
| Triángulo | equilátero | isósceles | escaleno |
|---|---|---|---|
| acutángulo |  |
 |
 |
| rectángulo |  |
 |
|
| obtusángulo |  |
 |
Triángulos iguales (Congruencia)
Congruencia de triángulos Dos triángulos son congruentes si son exactamente iguales en forma y tamaño. Esto significa que si los superpones, encajan perfectamente.
Reglas para saber si son congruentes
Hay algunas reglas que nos ayudan a saber si dos triángulos son congruentes sin tener que medir todos sus lados y ángulos:
| Triángulo | Reglas de congruencia |
|---|---|
 |
LAL (Lado, Ángulo, Lado)
Si dos lados y el ángulo entre ellos en un triángulo son iguales a los de otro triángulo, entonces son congruentes. |
 |
ALA (Ángulo, Lado, Ángulo)
Si dos ángulos y el lado entre ellos en un triángulo son iguales a los de otro triángulo, entonces son congruentes. |
 |
LLL (Lado, Lado, Lado)
Si los tres lados de un triángulo son iguales a los tres lados de otro triángulo, entonces son congruentes. |
También existe el teorema AAL (Ángulo, Ángulo, Lado), que dice que si dos ángulos y un lado no comprendido entre ellos son iguales, los triángulos son congruentes.
Triángulos parecidos (Semejanza)
Triángulos semejantes Dos triángulos son semejantes si tienen la misma forma, pero no necesariamente el mismo tamaño. Uno puede ser una versión más grande o más pequeña del otro. Sus ángulos son iguales y sus lados son proporcionales.
Reglas para saber si son semejantes
- AA (Ángulo, Ángulo): Si dos ángulos de un triángulo son iguales a dos ángulos de otro, son semejantes.
- LAL (Lado, Ángulo, Lado): Si dos lados son proporcionales y el ángulo entre ellos es igual, son semejantes.
- LLL (Lado, Lado, Lado): Si los tres lados son proporcionales, son semejantes.
Propiedades importantes de los triángulos
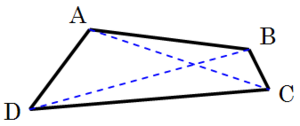
Un triángulo es el polígono más sencillo. Es la única figura con lados rectos que no tiene diagonal. Tres puntos que no están en la misma línea siempre forman un triángulo.
Si añades un cuarto punto en el mismo plano, puedes formar un cuadrilátero y dividirlo en triángulos. Si el cuarto punto no está en el mismo plano, puedes formar un tetraedro, que es una figura 3D con cuatro caras triangulares.
Cualquier figura con muchos lados (polígono) se puede dividir en triángulos.
La suma de los ángulos interiores
En la geometría que estudiamos normalmente (geometría euclidiana), la suma de los tres ángulos interiores de cualquier triángulo siempre es 180 grados.
Esto se puede demostrar dibujando una línea paralela a uno de los lados que pase por el vértice opuesto. Los ángulos que se forman te ayudarán a ver que la suma es 180°.
Otras propiedades
- La suma de las longitudes de dos lados de un triángulo siempre es mayor que la longitud del tercer lado.
- Los triángulos son siempre convexos, lo que significa que ninguno de sus ángulos puede ser mayor de 180 grados.
- El Teorema del seno dice que los lados de un triángulo son proporcionales a los senos de los ángulos opuestos.
- El Teorema del coseno relaciona la longitud de un lado con los otros dos lados y el coseno del ángulo entre ellos.
- Para los triángulos rectángulos, el famoso Teorema de Pitágoras dice que el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados (catetos):
.
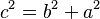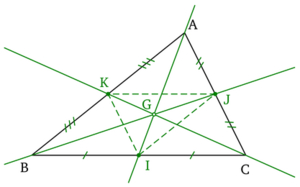
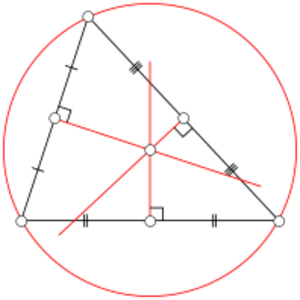
Puntos especiales en un triángulo
En un triángulo, hay varios puntos importantes:
- Baricentro: Es el punto donde se cruzan las medianas (líneas que van de un vértice al punto medio del lado opuesto). Es como el centro de equilibrio del triángulo.
- Circuncentro: Es el centro de la circunferencia que pasa por los tres vértices del triángulo. Se encuentra donde se cruzan las mediatrices (líneas perpendiculares a cada lado que pasan por su punto medio).
- Incentro: Es el centro de la circunferencia que está dentro del triángulo y toca sus tres lados. Se encuentra donde se cruzan las bisectrices (líneas que dividen cada ángulo en dos partes iguales).
- Ortocentro: Es el punto donde se cruzan las alturas (líneas perpendiculares que van de un vértice al lado opuesto).
En un triángulo equilátero, todos estos puntos coinciden en el mismo lugar.
Cómo calcular lados y ángulos
Para encontrar las medidas de los lados y ángulos de un triángulo, se usan diferentes herramientas:
- Para cualquier triángulo, se usan el Teorema del seno y el Teorema del coseno.
- Para triángulos rectángulos, se usa el Teorema de Pitágoras y las razones trigonométricas.
Razones trigonométricas en triángulos rectángulos
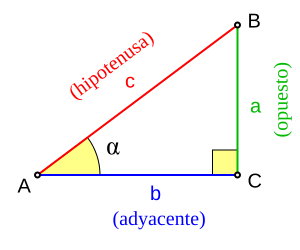
En los triángulos rectángulos, podemos usar el seno, coseno y tangente para encontrar lados y ángulos.
- La hipotenusa es el lado más largo, opuesto al ángulo recto.
- El cateto opuesto es el lado frente al ángulo agudo que estamos mirando.
- El cateto adyacente es el lado que está al lado del ángulo agudo que estamos mirando (sin ser la hipotenusa).
- Seno (sen): Cateto opuesto dividido por la hipotenusa.
- Coseno (cos): Cateto adyacente dividido por la hipotenusa.
- Tangente (tan): Cateto opuesto dividido por el cateto adyacente.
También existen las funciones inversas (arcsin, arccos, arctan) que nos permiten calcular los ángulos si conocemos las longitudes de los lados.
Elementos especiales de un triángulo
Mediana
Una mediana es un segmento de línea que va desde un vértice hasta el punto medio del lado opuesto.
- Las tres medianas de un triángulo se encuentran en un punto llamado baricentro.
- Cada mediana divide al triángulo en dos triángulos con la misma área.
- Las tres medianas dividen el triángulo en 6 triángulos más pequeños con áreas iguales.
Mediatriz y circunferencia circunscrita
La mediatriz de un lado es una línea perpendicular que pasa por el punto medio de ese lado.
Las tres mediatrices de un triángulo se encuentran en un punto llamado circuncentro. Este punto es el centro de la circunferencia circunscrita, que es la circunferencia que pasa por los tres vértices del triángulo.
- Si el triángulo es acutángulo, el circuncentro está dentro.
- Si es obtusángulo, está fuera.
- Si es rectángulo, está en el punto medio de la hipotenusa.
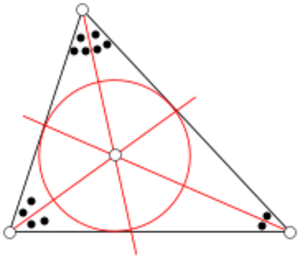
Bisectriz y circunferencias
Las bisectrices de un triángulo son las líneas que dividen cada ángulo interior en dos partes iguales.
Las tres bisectrices internas se encuentran en un punto llamado incentro. Este punto es el centro de la circunferencia inscrita, que es la circunferencia más grande que cabe dentro del triángulo y toca sus tres lados.
También hay circunferencias exinscritas que tocan un lado y las prolongaciones de los otros dos.
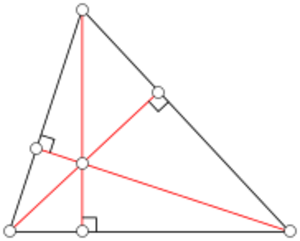
Alturas y ortocentro
Una altura de un triángulo es un segmento de línea perpendicular que va desde un vértice hasta el lado opuesto (o su prolongación). El lado opuesto se llama base.
Las tres alturas de un triángulo se cruzan en un punto único llamado ortocentro.
- Si el triángulo es rectángulo, el ortocentro es el vértice del ángulo recto.
- Si es obtusángulo, el ortocentro está fuera del triángulo.
- Si es acutángulo, el ortocentro está dentro del triángulo.
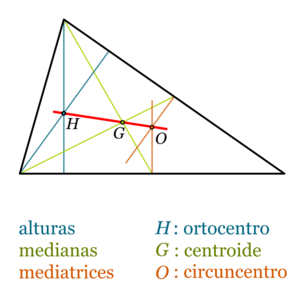
Recta de Euler
El ortocentro, el baricentro y el circuncentro de cualquier triángulo (excepto el equilátero) siempre están en una misma línea recta, llamada la recta de Euler.
Cómo calcular el área de un triángulo
Fórmula básica
La forma más común de calcular el área de un triángulo es multiplicando la longitud de su base por su altura y dividiendo el resultado entre dos.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac{\text{base} \times \text{altura}}{2}
Esta fórmula funciona para cualquier triángulo plano.
Fórmula de Herón
Fórmula de Herón Si conoces la longitud de los tres lados (a, b, c) de un triángulo, puedes calcular su área usando la Fórmula de Herón. Primero, calculas el semiperímetro (s), que es la mitad del perímetro:
Luego, aplicas la fórmula:
Área con dos lados y el ángulo entre ellos
Si conoces la longitud de dos lados y la medida del ángulo que está entre ellos, puedes usar esta fórmula:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathrm{\acute{A}rea} = \frac{a \times b \times \text{seno del ángulo C}}{2}
Donde 'a' y 'b' son los lados, y 'C' es el ángulo entre ellos.
Triángulos en el espacio
Los triángulos son las caras de algunos poliedros (figuras 3D con caras planas):
- tetraedro: Tiene 4 caras triangulares.
- octaedro: Tiene 8 caras triangulares.
- icosaedro: Tiene 20 caras triangulares.
Historia del triángulo
.png)
Los antiguos egipcios y mesopotámicos ya conocían mucho sobre los triángulos. Sus grandes construcciones, como las pirámides, muestran que tenían conocimientos avanzados de geometría.
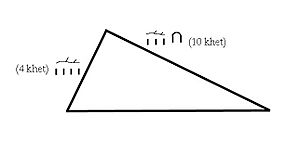
Uno de los documentos más antiguos que habla sobre el cálculo del área de un triángulo es el papiro Rhind, de Egipto, que data de hace miles de años. En él, se explica cómo calcular el área de un triángulo usando la fórmula de base por altura dividido entre dos, ¡igual que hoy!
También sabían que un triángulo con lados de 3, 4 y 5 unidades es un triángulo rectángulo.
Euclides, un matemático griego que vivió alrededor del año 300 antes de Cristo, demostró en su libro "Elementos" que la suma de los ángulos de un triángulo es siempre 180 grados.
Más sobre triángulos
- Relaciones métricas en el triángulo
- Congruencia de triángulos
- Triángulos semejantes
- Altura de un triángulo
- Teorema de la altura (para triángulos rectángulos)
- Vértice
- Teorema de Pitágoras
- Teorema de Tales
- Teorema del cateto
- Teorema del seno
- Teorema del coseno
- Teorema de Apolonio (teorema de las medianas)
- Teorema de Ceva
- Teorema de Routh
- Recta de Euler
- Anexo:Ecuaciones de figuras geométricas
- Fórmula de Herón
- Cateto
Tipos de triángulos especiales:
- triángulo equilátero, si tiene los tres ángulos y los tres lados iguales;
- triángulo rectángulo, si tiene uno de sus ángulos recto;
- triángulo de Kepler, un triángulo rectángulo especial relacionado con el número áureo;
- triángulo sagrado egipcio, un triángulo rectángulo con lados que miden 3, 4 y 5 unidades;
- triángulo esférico, si está en una superficie curva como una esfera;
- triángulo Bézier, una superficie geométrica con lados curvos;
- triángulo de Sierpinski, un patrón fractal que se forma a partir de un triángulo.
Véase también
En inglés: Triangle Facts for Kids
