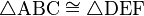Congruencia (geometría) para niños
En geometría, dos figuras u objetos son congruentes si tienen exactamente la misma forma y el mismo tamaño. Imagina que puedes mover, girar o voltear una figura y hacer que encaje perfectamente sobre la otra. Si lo logras, ¡son congruentes!
Esto significa que una figura puede transformarse en la otra mediante movimientos rígidos. Estos movimientos son:
- Una traslación: mover la figura de un lugar a otro sin girarla.
- Una rotación: girar la figura alrededor de un punto.
- Una reflexión: voltear la figura como si la vieras en un espejo.
Si dos figuras planas en un papel son congruentes, puedes recortar una y hacer que coincida por completo con la otra, incluso si tienes que darle la vuelta al papel.
La congruencia es un tipo de movimiento que mantiene las distancias y la orientación de las figuras.

En geometría básica, la palabra congruente se usa a menudo para describir:
- Dos segmentos de línea son congruentes si tienen la misma longitud.
- Dos ángulos son congruentes si tienen la misma medida.
- Dos círculos son congruentes si tienen el mismo diámetro.
Cuando decimos que "dos figuras planas son congruentes", esto implica que todas sus partes correspondientes son también congruentes o iguales. Esto incluye sus lados, ángulos, diagonales, perímetros y áreas.
El concepto de semejanza es parecido, pero se aplica cuando los objetos tienen la misma forma, pero no necesariamente el mismo tamaño. La congruencia es un caso especial de semejanza, donde el tamaño también es el mismo.
Contenido
- ¿Qué significa el concepto de congruencia?
- ¿Cómo determinar la congruencia de polígonos?
- ¿Cómo se define la congruencia en geometría analítica?
- Ángulos congruentes especiales
- Congruencia de triángulos
- ¿Pueden ser congruentes las secciones cónicas?
- ¿Y los poliedros congruentes?
- Galería de imágenes
- Véase también
¿Qué significa el concepto de congruencia?
Dos o más figuras son congruentes si son iguales en forma y tamaño. Esto significa que sus lados y ángulos correspondientes tienen la misma medida, aunque estén en posiciones u orientaciones diferentes.
El símbolo de congruencia es ( ≅ ).
Las partes que coinciden en figuras congruentes se llaman homólogas o correspondientes.
En matemáticas, dos figuras geométricas son congruentes si tienen las mismas dimensiones y la misma forma, sin importar su posición u orientación. Esto ocurre si una isometría (una transformación como traslación, rotación o reflexión) las relaciona. Las partes que se corresponden entre figuras congruentes se llaman homólogas o correspondientes.
¿Cómo determinar la congruencia de polígonos?
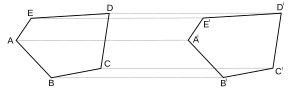
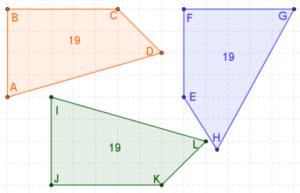
Para que dos polígonos sean congruentes, deben tener el mismo número de lados y de vértices. Dos polígonos con n lados son congruentes si tienen secuencias idénticas de lado-ángulo-lado-ángulo-... para sus n lados y n ángulos. Esta secuencia puede ser en el sentido de las agujas del reloj para un polígono y en sentido contrario para el otro.
Puedes verificar la congruencia de polígonos siguiendo estos pasos:
- Primero, empareja y etiqueta los vértices que se corresponden en ambas figuras.
- Segundo, dibuja una flecha (vector) desde un vértice de la primera figura hasta su vértice correspondiente en la segunda. Luego, traslada la primera figura usando esta flecha para que esos dos vértices coincidan.
- Tercero, gira la figura trasladada alrededor del vértice que ahora coincide, hasta que un par de lados correspondientes también coincidan.
- Cuarto, refleja la figura girada sobre este lado que coincide, hasta que ambas figuras se superpongan exactamente.
Si en algún momento no puedes completar un paso, los polígonos no son congruentes.
¿Cómo se define la congruencia en geometría analítica?
En la geometría euclidiana, la congruencia es como la igualdad en aritmética y álgebra. En geometría analítica, podemos definir la congruencia de forma sencilla: dos figuras dibujadas en un sistema de coordenadas cartesianas son congruentes si la distancia euclidiana entre cualquier par de puntos de la primera figura es igual a la distancia entre los puntos correspondientes de la segunda figura.
Más formalmente, dos conjuntos de puntos A y B en un espacio euclídeo se llaman congruentes si existe una isometría que transforma A en B. La congruencia es una relación de equivalencia, lo que significa que cumple ciertas propiedades (reflexiva, simétrica y transitiva).
Ángulos congruentes especiales
Algunos ángulos son siempre congruentes debido a su posición:
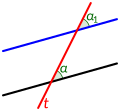
- Los ángulos opuestos por el vértice son congruentes. Si giras 180° uno de ellos alrededor de su vértice, coincidirá con el otro.
- Una recta que corta dos paralelas crea varios pares de ángulos congruentes.
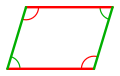
- Los ángulos opuestos de un paralelogramo son congruentes.
Congruencia de triángulos
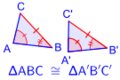
Dos triángulos son congruentes cuando sus lados correspondientes tienen la misma longitud y sus ángulos correspondientes tienen la misma medida.
Simbólicamente, escribimos la congruencia de dos triángulos △ABC y △A′B′C′ así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ABC\cong A'B'C'
Y si no son congruentes:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ABC\ncong A'B'C'
Para demostrar que dos triángulos son congruentes, no siempre necesitas conocer todas sus seis partes (tres lados y tres ángulos). A menudo, basta con conocer solo tres partes específicas.
Notación: Si dos triángulos 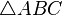 y
y 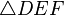 son congruentes, se escribe:
son congruentes, se escribe:
Criterios para la congruencia de triángulos
Existen reglas o "criterios" que nos permiten saber si dos triángulos son congruentes con la menor cantidad de información posible.
1. Caso ALA (Ángulo-Lado-Ángulo) o AAL (Ángulo-Ángulo-Lado): Dos triángulos son congruentes si tienen dos de sus ángulos respectivos iguales y el lado entre ellos también es igual. Si conoces dos ángulos de un triángulo, el tercer ángulo ya está determinado.
2. Caso LAL (Lado-Ángulo-Lado): Dos triángulos son congruentes si tienen dos lados iguales y el ángulo que está entre esos dos lados también es igual.
3. Caso LLL (Lado-Lado-Lado): Dos triángulos son congruentes si sus tres lados son iguales.
4. Caso LLA (Lado-Lado-Ángulo): Esta condición (dos lados y un ángulo que no está entre ellos) no siempre garantiza la congruencia. Para que funcione, se necesita más información, como que el triángulo sea un triángulo rectángulo o que el lado opuesto al ángulo sea más largo que el lado adyacente. Por ejemplo, en un triángulo rectángulo, si la hipotenusa y un cateto son iguales en ambos triángulos, entonces son congruentes (conocido como criterio HL o Hipotenusa-Cateto).
¿Por qué Ángulo-Ángulo-Ángulo (AAA) no es suficiente para la congruencia?
En la geometría euclidiana, si dos triángulos tienen los mismos tres ángulos (AAA), solo podemos decir que son similares, no necesariamente congruentes. Esto se debe a que pueden tener la misma forma, pero tamaños diferentes. Por ejemplo, un triángulo pequeño y uno grande pueden tener los mismos ángulos.
Sin embargo, en otras geometrías (como la esférica o la hiperbólica), AAA sí es suficiente para la congruencia.
CPCTC: Partes correspondientes de triángulos congruentes son congruentes
Este acrónimo viene del inglés Corresponding Parts of Congruent Triangles are Congruent. Significa que si dos triángulos son congruentes, entonces todas sus partes correspondientes (lados y ángulos) también son congruentes.
Por ejemplo, si los triángulos ABC y DEF son congruentes, es decir:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \triangle ABC \cong \triangle DEF,
con los vértices A y D correspondientes, B y E correspondientes, y C y F correspondientes, entonces se cumplen estas afirmaciones:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \overline{AB} \cong \overline{DE} (el lado AB es congruente con DE)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \overline{BC} \cong \overline{EF} (el lado BC es congruente con EF)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \overline{AC} \cong \overline{DF} (el lado AC es congruente con DF)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \angle BAC \cong \angle EDF (el ángulo BAC es congruente con EDF)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \angle ABC \cong \angle DEF (el ángulo ABC es congruente con DEF)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \angle BCA \cong \angle EFD. (el ángulo BCA es congruente con EFD)
Esta idea se usa mucho en las demostraciones de geometría. Si ya probaste que dos triángulos son congruentes (por ejemplo, usando LLL), y luego necesitas demostrar que uno de sus ángulos correspondientes es igual, puedes usar CPCTC como justificación.
Existe un teorema similar llamado CPCFC, donde "triángulos" se reemplaza por "figuras", y se aplica a cualquier par de polígonos o poliedros que sean congruentes.
¿Pueden ser congruentes las secciones cónicas?
Sí, dos secciones cónicas (como círculos, parábolas o hipérbolas) son congruentes si tienen la misma excentricidad (que define su forma) y otro parámetro que define su tamaño. Por ejemplo, dos circunferencias son congruentes si tienen el mismo radio (o diámetro).
¿Y los poliedros congruentes?
Para dos poliedros (figuras 3D con caras planas) que tienen el mismo tipo de caras y aristas, se necesita un conjunto de medidas para saber si son congruentes. Por ejemplo, los cubos tienen 12 aristas, pero con solo 9 medidas se puede decidir si un poliedro es congruente con un cubo regular.
Galería de imágenes
Véase también
 En inglés: Congruence (geometry) Facts for Kids
En inglés: Congruence (geometry) Facts for Kids


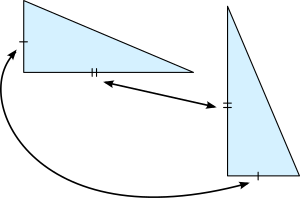
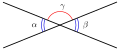
 y
y 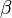 son congruentes y opuestos por el vértice.
son congruentes y opuestos por el vértice.