Triángulo de Sierpinski para niños
El triángulo de Sierpinski es una figura geométrica muy especial, conocida como fractal. Un fractal es una forma que se repite a sí misma en diferentes tamaños, como si pudieras hacerle zoom y siempre vieras el mismo patrón. Este triángulo se puede construir a partir de cualquier triángulo.
Contenido
¿Quién creó el Triángulo de Sierpinski?
El matemático polaco Waclaw Sierpinski (nacido en Varsovia en 1882 y fallecido en 1969) fue quien ideó este famoso triángulo, entre otras figuras fractales. Su trabajo nos ayuda a entender cómo las formas complejas pueden surgir de reglas sencillas que se repiten.
¿Cómo se construye el Triángulo de Sierpinski?
La construcción de este triángulo es como un juego de ir quitando partes. Imagina que tienes un triángulo y sigues estos pasos:
Pasos para construir el Triángulo de Sierpinski
- Paso 1: El primer corte. Empieza con un triángulo grande, por ejemplo, un triángulo equilátero (todos sus lados son iguales). Encuentra el punto medio de cada lado y únelos. Esto formará un triángulo más pequeño justo en el centro. ¡Quita ese triángulo central! Te quedarán tres triángulos más pequeños en las esquinas.
- Paso 2: Repetir el proceso. Ahora, toma cada uno de esos tres triángulos pequeños que te quedaron. En cada uno de ellos, repite el mismo proceso: encuentra los puntos medios de sus lados, únelos y quita el triángulo central. Después de este paso, tendrás nueve triángulos aún más pequeños.
- Paso 3: Continuar sin parar. Sigue repitiendo este proceso una y otra vez en cada nuevo triángulo que aparece. Cuantas más veces lo hagas, más se parecerá la figura al verdadero triángulo de Sierpinski. Es un proceso que, en teoría, nunca termina.

¿Qué pasa con el área del triángulo?
Aunque parezca que siempre quedan triángulos, si pudieras repetir este proceso infinitas veces, ¡el área total de la figura que queda sería cero! Es como si el triángulo se convirtiera en una "nube" de puntos que están muy juntos, pero no forman una superficie sólida. Esto es una característica sorprendente de los fractales.
Construcción con funciones matemáticas
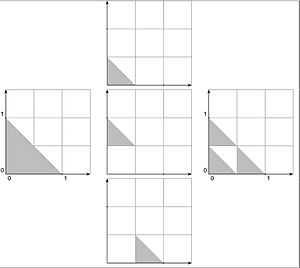
El triángulo de Sierpinski también se puede crear usando un método llamado "Sistema de Funciones Iteradas" (SFI).
¿Qué es un Sistema de Funciones Iteradas?
Un SFI es como una receta que usa varias instrucciones matemáticas para transformar una figura. Cada instrucción es una "función" que encoge y mueve la figura. Cuando aplicas estas funciones una y otra vez, la figura se va transformando hasta convertirse en el fractal.
Para el triángulo de Sierpinski, se usan tres funciones. Cada una de ellas encoge el triángulo a la mitad y lo mueve a una de las tres esquinas. Al juntar los resultados de estas tres funciones, se forma una versión más pequeña del triángulo de Sierpinski.
Lo más asombroso de los SFI es que, no importa con qué figura empieces (podría ser un cuadrado, una estrella o incluso un dibujo de un gato), si aplicas estas funciones una y otra vez, ¡siempre terminarás con el triángulo de Sierpinski! La forma inicial se "atrae" hacia el fractal.
Construcción con puntos aleatorios
Otra forma curiosa de dibujar el triángulo de Sierpinski es usando un método con puntos aleatorios, a veces llamado "juego del caos".
¿Cómo funciona el método de los puntos?
Imagina que tienes tres puntos que forman los vértices de un triángulo.
- Elige un punto cualquiera dentro del triángulo.
- Lanza un dado (o elige un número al azar) para seleccionar uno de los tres vértices del triángulo.
- Dibuja un nuevo punto exactamente a la mitad del camino entre tu punto actual y el vértice que elegiste al azar.
- Ahora, ese nuevo punto es tu "punto actual" y repite los pasos 2 y 3 miles de veces.
Si haces esto muchas veces, verás que los puntos que dibujas empiezan a formar el patrón del triángulo de Sierpinski.
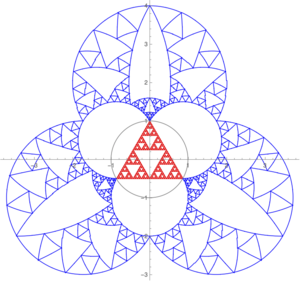
El Triángulo de Sierpinski y la inversión circular
La inversión circular es una transformación geométrica que cambia las figuras de una manera especial. Cuando aplicas la inversión circular al triángulo de Sierpinski, se crean imágenes muy bonitas y complejas que muestran cómo interactúan la geometría clásica y la geometría fractal.
¿Cuál es la dimensión del Triángulo de Sierpinski?
Normalmente, una línea tiene 1 dimensión y una superficie (como un cuadrado) tiene 2 dimensiones. Pero los fractales tienen una "dimensión fractal" que puede ser un número con decimales. El triángulo de Sierpinski tiene una dimensión fractal de aproximadamente 1.585. Esto significa que es más que una línea, pero menos que una superficie completa, lo cual es otra de sus características fascinantes.
Véase también
 En inglés: Sierpiński triangle Facts for Kids
En inglés: Sierpiński triangle Facts for Kids