Teorema del seno para niños
En el mundo de la trigonometría plana, existe una regla muy útil llamada el Teorema del Seno o Ley de los Senos. Esta regla nos muestra una relación especial entre los lados de un triángulo y los senos de sus ángulos opuestos. Es como una proporción que siempre se cumple.
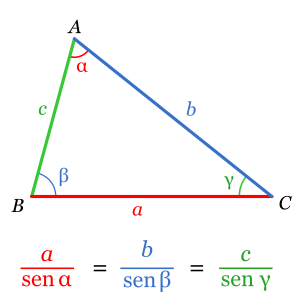
Imagina un triángulo llamado ABC. Sus ángulos internos son α (alfa), β (beta) y γ (gamma). Los lados opuestos a estos ángulos se llaman a, b y c respectivamente. El Teorema del Seno dice que si divides la longitud de un lado por el seno de su ángulo opuesto, ¡el resultado siempre será el mismo para los tres lados!
|
Contenido
Un Viaje en el Tiempo: La Historia del Teorema
El Teorema del Seno tiene una historia interesante que se remonta a muchos siglos atrás.
¿Quiénes lo Descubrieron?
Se cree que la versión para triángulos en una esfera (llamada ley esférica de los senos) fue descubierta en el siglo X. Varios matemáticos importantes de esa época, como Abu-Mahmud Khojandi, Abu al-Wafa' Buzjani, Nasir al-Din al-Tusi y Abu Nasr Mansur, son mencionados como posibles descubridores.
En el siglo XI, un matemático llamado Ibn Muʿādh al-Jayyānī escribió un libro donde presentó la ley general de los senos. Más tarde, en el siglo XIII, Nasīr al-Dīn al-Tūsī describió la ley para triángulos planos en su obra Sobre la figura del sector, donde también dio pruebas de esta ley.
También se menciona a Johann Regiomontanus, un matemático alemán del siglo XV, quien usó la ley de los senos en sus soluciones para diferentes tipos de triángulos.
¿Cómo se Demuestra este Teorema?
Aunque es uno de los teoremas más usados en trigonometría, su demostración es bastante sencilla y no siempre se explica en los cursos.
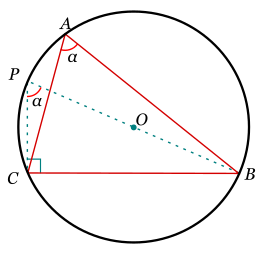
Imagina un triángulo ABC. Podemos dibujar un círculo que pase por sus tres vértices. Este círculo se llama circunferencia circunscrita, y su centro se llama circuncentro (lo llamaremos O).
Si dibujamos una línea desde el vértice B que pase por el centro O y llegue al otro lado del círculo, obtenemos un diámetro BP. El triángulo PCB es un triángulo rectángulo (tiene un ángulo de 90 grados) porque BP es un diámetro.
Además, los ángulos A y P son iguales. Esto es porque ambos son ángulos inscritos que "abren" el mismo segmento BC del círculo.
Usando la definición de la función seno en el triángulo PCB, tenemos que el seno del ángulo P es igual al lado opuesto (BC, que es a) dividido por la hipotenusa (BP, que es el diámetro del círculo, o sea, 2R, donde R es el radio).
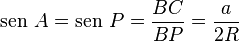
Si reorganizamos esta ecuación, obtenemos:
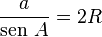
Si hacemos lo mismo para los otros lados y ángulos del triángulo, veremos que la misma relación se cumple. Esto significa que las tres fracciones son iguales al mismo valor, que es el diámetro de la circunferencia circunscrita.
Esta es la forma generalizada del Teorema del Seno:
|
En resumen, el teorema dice que en cualquier triángulo, la división de cada lado por el seno de su ángulo opuesto siempre da el mismo resultado, y ese resultado es igual al diámetro del círculo que pasa por los tres vértices del triángulo.
¿Para Qué Sirve el Teorema del Seno?
El Teorema del Seno es muy útil para resolver problemas con triángulos.
¿Cuándo se Utiliza?
Se usa principalmente en dos situaciones:
- Cuando conoces dos ángulos de un triángulo y la medida de cualquiera de sus lados.
- Cuando conoces dos lados del triángulo y el ángulo opuesto a uno de esos lados.
Ejemplos de Aplicación
La Ley de los Senos se puede aplicar en muchas situaciones prácticas, como:
- Calcular la altura de objetos altos como árboles o edificios.
- Determinar el ángulo de elevación del suelo en un terreno.
- Ayudar en el diseño y la construcción de puentes.
- Estudiar y dibujar los caminos de una autopista.
- Planificar la ruta de un planeador.
- Localizar la posición de un punto específico, como un foco de incendio.
- Resolver problemas que involucran vectores (cantidades con dirección y magnitud).
- Calcular la altitud de una montaña.
El Teorema del Seno y el Área del Triángulo
El Teorema del Seno también nos ayuda a encontrar el área de un triángulo de una manera diferente.
Normalmente, el área de un triángulo se calcula multiplicando la base por la altura y dividiendo entre dos (Area = ah/2). Si usamos la definición de seno, podemos decir que la altura h es igual a b multiplicado por el seno del ángulo C (h = b sen C).
Así, el área también se puede calcular como:
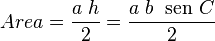 .
.
Pero, como el Teorema del Seno nos dice que c = 2R sen C, podemos reemplazar sen C en la fórmula del área. Esto nos da una nueva forma de calcular el área:
|
Esta fórmula es muy útil cuando conocemos los tres lados del triángulo y el radio del círculo que lo rodea.
Véase también
 En inglés: Law of sines Facts for Kids
En inglés: Law of sines Facts for Kids
- Trigonometría
- Triangulación
- Trigonometría esférica
- Función trigonométrica
- Geometría del triángulo
- Teorema del coseno
- Teorema de Pitágoras


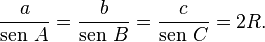
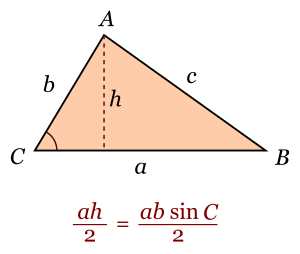
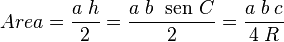 .
.