Teoremas de incompletitud de Gödel para niños

Los teoremas de incompletitud de Gödel son dos ideas muy importantes en la lógica matemática, que fueron demostradas por un matemático llamado Kurt Gödel en 1931. Estos teoremas nos dicen que hay límites en lo que podemos probar dentro de ciertos sistemas matemáticos. Se relacionan con la existencia de afirmaciones que no se pueden decidir (ni probar ni refutar) en algunas teorías que describen los números naturales.
Contenido
¿Qué son los Teoremas de Incompletitud de Gödel?
El Primer Teorema de Incompletitud
El primer teorema de incompletitud nos dice que si tenemos una teoría matemática formal (un conjunto de reglas y símbolos para hacer matemáticas) que es lo suficientemente potente como para describir los números naturales y sus operaciones (como sumar y multiplicar), entonces no puede ser a la vez:
- Consistente: Que no tenga contradicciones. Es decir, que no se pueda probar que algo es verdadero y falso al mismo tiempo.
- Completa: Que pueda probar o refutar cualquier afirmación dentro de ella.
En otras palabras, si los axiomas (las reglas básicas) de esa teoría no se contradicen entre sí, entonces siempre habrá afirmaciones que no se podrán probar ni refutar usando solo esas reglas. Es como si hubiera preguntas que el sistema no puede responder por sí mismo. Esto se aplica si el sistema puede seguir un algoritmo, es decir, una serie de pasos claros y definidos.
El Segundo Teorema de Incompletitud
El segundo teorema de incompletitud es una consecuencia del primero. Afirma que una de las afirmaciones que no se pueden decidir en una teoría así es precisamente la que dice que la teoría es consistente (que no tiene contradicciones). Esto significa que si un sistema de reglas matemáticas es consistente, no es posible demostrar esa consistencia usando solo las reglas de ese mismo sistema. Es como si el sistema no pudiera probar su propia perfección.
Estos teoremas de Gödel son considerados uno de los avances más grandes en la lógica matemática. Mostraron que los sistemas de reglas matemáticas tienen limitaciones importantes para ser la base de todas las matemáticas.
¿Por qué son importantes estos teoremas?
Entendiendo las Teorías Formales
Para entender mejor los teoremas de Gödel, necesitamos saber qué es una "teoría formal". Imagina que es un juego con reglas muy estrictas. Una teoría formal tiene:
- Un conjunto de símbolos (como números, signos de suma, etc.).
- Un conjunto de reglas para combinar esos símbolos y formar "fórmulas" (como oraciones matemáticas).
- Un conjunto de reglas para demostrar que algunas fórmulas son "teoremas" (como verdades que se pueden probar).
Los axiomas son las fórmulas iniciales que se aceptan como verdaderas sin necesidad de demostración.
Propiedades de las Teorías Formales
Las teorías formales pueden tener ciertas propiedades:
- Consistente: Una teoría es consistente si no contiene contradicciones. Es decir, no puedes probar una afirmación y su opuesto al mismo tiempo. Si una teoría no es consistente, no sirve de mucho, porque podrías probar cualquier cosa.
- Completa: Una teoría es completa si puede responder a cualquier pregunta. Esto significa que para cada afirmación, o bien se puede probar que es verdadera, o bien se puede probar que es falsa.
El primer teorema de incompletitud de Gödel nos dice que, bajo ciertas condiciones, una teoría formal no puede tener ambas propiedades a la vez. Las condiciones son:
- Que sea una teoría aritmética: Que sus símbolos puedan describir los números naturales y sus operaciones básicas.
- Que sea una teoría recursiva: Que las reglas para manipular los símbolos y las fórmulas puedan ejecutarse mediante un algoritmo (un conjunto de pasos claros y finitos, como un programa de computadora).
El Primer Teorema de Incompletitud en Detalle
El primer teorema de incompletitud de Gödel dice:
|
Para demostrar esto, Gödel construyó una fórmula especial, a la que se le llama la "sentencia de Gödel" (representada como G). Esta fórmula es muy particular: no se puede probar ni refutar dentro de la teoría matemática. Es decir, ni G ni su negación (¬G) son teoremas de la teoría. Se dice que G es una afirmación indecidible o independiente.
¿Cómo se construye la Sentencia de Gödel?
Gödel usó un método llamado "numeración de Gödel". Imagina que a cada símbolo, cada fórmula y cada demostración en matemáticas se le asigna un número único. Así, las propiedades de las fórmulas y las demostraciones se pueden traducir a propiedades de números.
La sentencia de Gödel G es una fórmula matemática cuyo significado es: "No existe una demostración de G en esta teoría". En otras palabras, G dice: "Yo no puedo ser demostrada en esta teoría".
Consecuencias del Primer Teorema
La sentencia de Gödel G no se puede demostrar, pero es verdadera, porque precisamente afirma que no se puede demostrar, ¡y así es! Esto significa que ninguna teoría aritmética que cumpla las condiciones del teorema puede demostrar todas las afirmaciones verdaderas sobre los números naturales. Siempre habrá verdades que no se puedan alcanzar con ese sistema de reglas.
El Segundo Teorema de Incompletitud en Detalle
El segundo teorema de incompletitud nos da otro ejemplo de una fórmula que ninguna teoría aritmética puede demostrar. Usando la numeración de Gödel, se puede crear una fórmula llamada "Consis T", que significa: "No se puede encontrar una contradicción en la teoría T", o sea, "La teoría T es consistente".
|
Esto significa que una teoría matemática no puede probar su propia consistencia. Si pudiera, eso llevaría a una contradicción con el primer teorema.
Consecuencias del Segundo Teorema
El segundo teorema de incompletitud nos dice que no podemos demostrar que un sistema formal es consistente usando solo las reglas de ese mismo sistema. Si queremos probar la consistencia de un sistema, necesitamos usar un sistema más potente, pero la consistencia de ese sistema más potente tampoco podrá probarse dentro de sí mismo. Esto fue un golpe para la idea de que se podría crear un sistema matemático perfecto que lo abarcara todo y probara su propia validez.
Afirmaciones Indecidibles
Los teoremas de Gödel demuestran que existen afirmaciones que no se pueden decidir en la aritmética. Además de la sentencia de Gödel y la afirmación de consistencia, se han encontrado otros ejemplos de afirmaciones que son independientes de los axiomas de Peano (un conjunto de axiomas para los números naturales).
También hay ejemplos de afirmaciones indecidibles en otras teorías matemáticas, como la hipótesis del continuo en la teoría de conjuntos, o el postulado de las paralelas en la geometría euclídea.
Reflexiones e Implicaciones
Los resultados de Gödel tienen un gran impacto en la filosofía de las matemáticas. Una forma sencilla de entender el primer teorema es que "nunca podremos encontrar un sistema de reglas matemáticas que sea capaz de demostrar todas las verdades matemáticas y ninguna falsedad".
El segundo teorema, reformulado, es aún más sorprendente: "Si se puede demostrar que un sistema de reglas es consistente usando solo sus propias reglas, entonces ese sistema es inconsistente". Esto significa que para estar seguros de que un sistema es consistente, necesitamos una prueba que venga de "fuera" de ese sistema.
Los teoremas de Gödel solo se aplican a sistemas de reglas que son "suficientemente fuertes", es decir, que tienen la capacidad de describir la aritmética básica (suma y multiplicación). Hay sistemas más simples que sí pueden ser consistentes y completos.
El trabajo de Gödel también inspiró a Alan Turing a investigar qué problemas pueden ser resueltos por una computadora y cuáles no. Turing demostró que existen problemas que ninguna computadora puede resolver, como el famoso "Problema de parada", que pregunta si un programa de computadora terminará de ejecutarse o seguirá calculando indefinidamente.
En esencia, la prueba del primer teorema de Gödel es como una versión matemática de la paradoja del mentiroso ("Esta frase es falsa"). La sentencia de Gödel dice: "Esta afirmación no se puede probar". Si fuera demostrable, entonces sería falsa (porque dice que no se puede probar), lo que es una contradicción. Si no es demostrable, entonces es verdadera (porque dice que no se puede probar, y así es). Por lo tanto, es una verdad que no se puede probar dentro del sistema.
Algunos pensadores, como Roger Penrose, han sugerido que esta diferencia entre lo que se puede probar con reglas mecánicas y lo que los humanos pueden entender como verdadero, podría significar que la inteligencia humana no es puramente mecánica. Sin embargo, esta idea no es aceptada por todos.
Galería de imágenes
Véase también


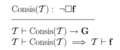
 En inglés:
En inglés: