Teorema de Taylor para niños
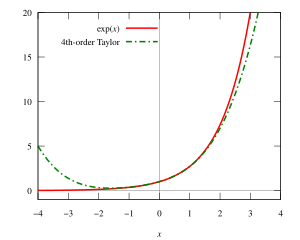
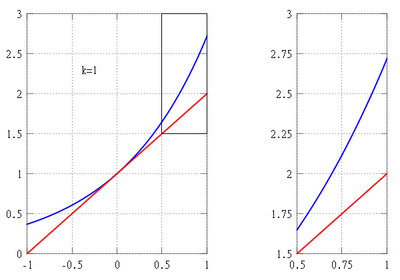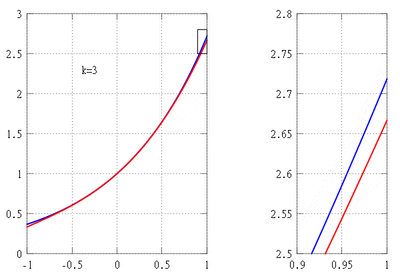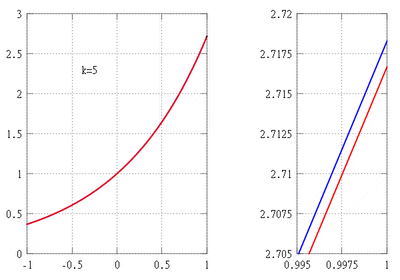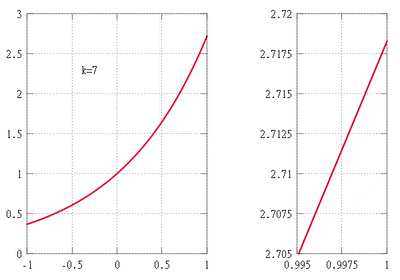
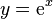 (línea roja continua) y su aproximación mediante un polinomio de Taylor alrededor del origen de coordenadas (línea verde discontinua)
(línea roja continua) y su aproximación mediante un polinomio de Taylor alrededor del origen de coordenadas (línea verde discontinua)El teorema de Taylor es una herramienta muy importante en el cálculo diferencial. Lleva el nombre del matemático británico Brook Taylor, quien lo presentó de forma más completa en 1712. Sin embargo, otro matemático, James Gregory, ya lo había descubierto en 1671.
Este teorema nos permite crear "polinomios" que se parecen mucho a una función más complicada. Es como si usáramos un dibujo sencillo (el polinomio) para representar un dibujo más complejo (la función original) en un lugar específico. Además, el teorema nos ayuda a saber qué tan preciso es ese dibujo sencillo, es decir, cuánto error tiene nuestra aproximación.
|
Contenido
¿Qué es el Teorema de Taylor?
El teorema de Taylor nos ayuda a aproximar funciones. Una función es como una máquina matemática que toma un número y lo transforma en otro. Por ejemplo, la función 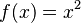 toma el 3 y lo convierte en 9.
toma el 3 y lo convierte en 9.
Polinomios de Taylor: Aproximaciones Útiles
Un polinomio es una expresión matemática más sencilla, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 + 2x + 1 . El teorema de Taylor nos dice que podemos usar un polinomio para "imitar" el comportamiento de una función más compleja cerca de un punto específico.
El polinomio que se usa para esta aproximación se llama polinomio de Taylor. Cuanto más alto sea el "orden" de este polinomio (es decir, cuantas más partes tenga), mejor será la aproximación.
La parte que nos dice cuánto nos equivocamos al usar el polinomio se llama término del resto. Es la diferencia entre el valor real de la función y el valor que nos da el polinomio.
¿Cómo se calcula el error de la aproximación?
Existen diferentes maneras de calcular este "término del resto" para saber qué tan buena es nuestra aproximación. Algunas de las formas más conocidas son:
- Forma de Lagrange del resto: Esta forma nos da una idea de dónde podría estar el error.
- Forma de Cauchy del resto: Es otra manera de expresar el error, similar a la de Lagrange.
- Forma integral del resto: Esta forma usa integrales para calcular el error, lo que es útil en matemáticas más avanzadas.
Estas fórmulas nos permiten poner un límite al error. Así, podemos estar seguros de que nuestra aproximación es lo suficientemente precisa para lo que la necesitamos.
Ejemplo Práctico: Aproximando la función ex
Imagina que queremos calcular el valor de la función 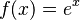 (la función exponencial) con mucha precisión, por ejemplo, con un error menor a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0.00001 .
(la función exponencial) con mucha precisión, por ejemplo, con un error menor a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0.00001 .
Sabemos que la función 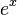 tiene una propiedad especial: su derivada (la forma en que cambia) es siempre ella misma,
tiene una propiedad especial: su derivada (la forma en que cambia) es siempre ella misma, 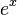 . También sabemos que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^0 = 1 .
. También sabemos que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^0 = 1 .
Usando el teorema de Taylor, podemos construir un polinomio que se parezca a 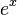 cerca del punto
cerca del punto 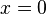 : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P_k(x) = 1+x+\frac{x^2}{2!}+\cdots+\frac{x^k}{k!}
: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P_k(x) = 1+x+\frac{x^2}{2!}+\cdots+\frac{x^k}{k!}
Y el error de esta aproximación es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): R_k(x)=\frac{e^\xi}{(k+1)!}x^{k+1} donde 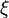 es un número entre
es un número entre 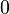 y
y  .
.
Para que el error sea menor a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0.00001 en el intervalo de 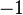 a
a 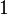 , necesitamos que el polinomio tenga al menos 9 términos (es decir, que
, necesitamos que el polinomio tenga al menos 9 términos (es decir, que 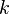 sea igual o mayor que 9).
sea igual o mayor que 9).
Así, podemos aproximar 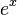 con mucha precisión: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^x = 1+x+\frac{x^2}{2!} + \cdots + \frac{x^9}{9!} + R_9(x) donde el error Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |R_9(x)| es menor a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0.00001 .
con mucha precisión: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^x = 1+x+\frac{x^2}{2!} + \cdots + \frac{x^9}{9!} + R_9(x) donde el error Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |R_9(x)| es menor a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0.00001 .
Gracias a esto, podemos calcular el valor de  (que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^1 ) como aproximadamente Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2.71828 , ¡con cinco decimales correctos!
(que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^1 ) como aproximadamente Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2.71828 , ¡con cinco decimales correctos!
Teorema de Taylor para varias variables
El teorema de Taylor no solo funciona para funciones que dependen de una sola variable (como  ), sino que también se puede usar para funciones que dependen de varias variables (como
), sino que también se puede usar para funciones que dependen de varias variables (como  ,
,  y
y 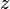 ).
).
La idea es la misma: aproximar una función compleja con un polinomio más sencillo. Sin embargo, las fórmulas se vuelven un poco más complicadas porque hay que considerar cómo la función cambia en todas las direcciones.
Véase también
 En inglés: Taylor's theorem Facts for Kids
En inglés: Taylor's theorem Facts for Kids


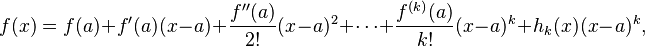
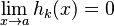 . Esta es la llamada forma de
. Esta es la llamada forma de