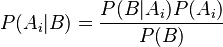Teorema de Bayes para niños
El teorema de Bayes es una idea muy importante en la teoría de la probabilidad. Fue propuesta por un matemático inglés llamado Thomas Bayes hace mucho tiempo, en el siglo XVIII. Este teorema nos ayuda a entender cómo cambia la probabilidad de que algo ocurra cuando tenemos nueva información.
Imagina que quieres saber la probabilidad de que llueva (evento A) si ves nubes oscuras (evento B). El teorema de Bayes te permite usar la probabilidad de ver nubes oscuras si llueve para calcular la probabilidad de que llueva si ves nubes oscuras. Es como una herramienta que conecta dos tipos de probabilidades: la probabilidad de un evento dado otro, y la probabilidad del segundo evento dado el primero. Esto es muy útil en muchas áreas de la ciencia, porque nos ayuda a entender las causas de las cosas basándonos en lo que observamos.
Una de las formas más importantes de usar el teorema de Bayes es en la inferencia bayesiana. Esta es una manera especial de hacer inferencia estadística, que es como sacar conclusiones de los datos. Cuando usamos el teorema de Bayes, las probabilidades pueden interpretarse de diferentes maneras. Para algunos, el teorema muestra cómo nuestra creencia en algo (expresada como una probabilidad) debería cambiar de forma lógica cuando tenemos nuevas pruebas o información. La inferencia bayesiana es tan fundamental para la estadística bayesiana que se ha dicho que es "a la teoría de la probabilidad lo que el teorema de Pitágoras es a la geometría".
Contenido
Historia del Teorema de Bayes
El teorema lleva el nombre del reverendo Thomas Bayes, quien también era un experto en estadística y filosofía. Bayes usó la idea de la probabilidad condicional para crear un método que usa la información disponible para calcular los límites de un valor desconocido. Su trabajo se publicó en 1763, después de su fallecimiento, con el título Un ensayo para resolver un problema de la doctrina de las probabilidades. Bayes investigó cómo calcular una distribución para el parámetro de probabilidad de una distribución binomial.
Cuando Bayes murió, su familia entregó sus escritos a un amigo, el ministro, filósofo y matemático Richard Price. Durante dos años, Richard Price revisó y editó el manuscrito de Bayes antes de enviarlo a un amigo para que lo leyera en la Royal Society el 23 de diciembre de 1763. Price escribió una introducción al documento que explica algunas de las ideas filosóficas detrás de la estadística bayesiana. En 1765, Price fue elegido miembro de la Royal Society por su importante trabajo con el legado de Bayes.
De forma independiente a Bayes, el científico Pierre-Simon Laplace también trabajó en ideas similares. En 1774, y más tarde en su libro Théorie analytique des probabilités de 1812, Laplace usó la probabilidad condicional para explicar cómo una probabilidad actualizada (llamada probabilidad posterior) se obtiene de una probabilidad anterior, cuando se tiene nueva información. Él reprodujo y amplió los resultados de Bayes en 1774, sin saber del trabajo de Bayes en ese momento. Laplace mejoró el teorema de Bayes a lo largo de varias décadas. La interpretación bayesiana de la probabilidad fue desarrollada principalmente por Laplace.
Casi 200 años después, Sir Harold Jeffreys estableció el método de Bayes y la formulación de Laplace sobre una base sólida, como un sistema axiomático. En un libro de 1973, escribió que el teorema de Bayes "es a la teoría de la probabilidad lo que el teorema de Pitágoras es a la geometría".
Algunos historiadores, como Stephen Stigler, han sugerido que el teorema de Bayes pudo haber sido descubierto antes por Nicholas Saunderson, un matemático inglés ciego. Sin embargo, esta idea ha sido debatida. Martyn Hooper y Sharon McGrayne han argumentado que la contribución de Richard Price fue muy importante. Ellos creen que deberíamos referirnos a la "regla de Bayes-Price", porque Price descubrió el trabajo de Bayes, vio su importancia, lo corrigió, contribuyó al artículo y le encontró un uso práctico.
¿Cómo funciona el Teorema de Bayes?
El teorema de Bayes se expresa con una fórmula matemática. Imagina que tienes un grupo de eventos que no pueden ocurrir al mismo tiempo y que cubren todas las posibilidades (como si un día llueve, está nublado o hace sol, y solo puede ser una de esas cosas). Si conoces la probabilidad de que ocurra un evento B, dado que ocurrió uno de esos eventos iniciales, el teorema de Bayes te ayuda a calcular la probabilidad de que uno de esos eventos iniciales haya ocurrido, dado que ya sabes que el evento B sucedió.
La fórmula se ve así:
Donde:
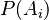son las probabilidades a priori, que son tus creencias iniciales sobre la probabilidad de cada evento 
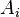antes de tener nueva información.
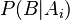es la probabilidad de que ocurra el evento 
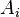si ya sabes que el evento ocurrió.
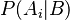son las probabilidades a posteriori, que son las probabilidades actualizadas de cada evento 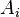después de que sabes que el evento ocurrió.
Aplicaciones del Teorema de Bayes
El teorema de Bayes es útil en todas las áreas donde se usa la teoría de la probabilidad. Sin embargo, hay un debate sobre qué tipo de probabilidades se deben usar. Algunos expertos en estadística solo aceptan probabilidades que se basan en experimentos que se pueden repetir y que tienen pruebas reales. Otros, llamados estadísticos bayesianos, permiten usar probabilidades que se basan en el conocimiento o la creencia personal, que luego se ajustan con nueva información.
El teorema de Bayes puede mostrar cómo debemos cambiar nuestras creencias iniciales cuando obtenemos información adicional de un experimento. La estadística bayesiana es muy útil para hacer estimaciones basadas en lo que ya sabemos, y la posibilidad de revisar esas estimaciones con pruebas reales está abriendo nuevas formas de entender el conocimiento.
Algunas aplicaciones prácticas del teorema de Bayes incluyen:
- Los clasificadores bayesianos, que se usan a menudo en los filtros de correo no deseado (spam) para aprender y adaptarse con el uso.
- La combinación de información de diferentes sensores, lo que se conoce como fusión de datos.
- El diagnóstico de ciertas condiciones médicas.
- La evaluación de probabilidades en juegos de cartas como el bridge.
- El estudio de probabilidades iniciales y finales en diferentes situaciones.
- El análisis de hipótesis en ciencias sociales.
- En la estadística bayesiana en general.
Uso en Genética
En genética, el teorema de Bayes se puede usar para calcular la probabilidad de que una persona tenga un genotipo específico. Muchas personas quieren saber sus posibilidades de tener una enfermedad genética o de ser portadoras de un gen que podría causar una enfermedad. Se puede hacer un análisis bayesiano usando la información de los antecedentes familiares o de pruebas genéticas. Esto ayuda a predecir si una persona desarrollará una enfermedad o si la transmitirá a sus hijos. Las pruebas y predicciones genéticas son comunes entre parejas que planean tener hijos y están preocupadas por la posibilidad de que ambos sean portadores de una enfermedad, especialmente en comunidades donde hay poca variación genética.
El primer paso en un análisis bayesiano para la genética es proponer ideas que no pueden ser ciertas al mismo tiempo. Por ejemplo, para un alelo específico, una persona es portadora o no lo es. Luego, se calculan cuatro tipos de probabilidades:
- Probabilidad Previa: La probabilidad de cada idea antes de tener nueva información, considerando los antecedentes familiares o las predicciones basadas en la Herencia Mendeliana.
- Probabilidad Condicional: La probabilidad de un resultado específico si una de las ideas es cierta.
- Probabilidad Conjunta: El resultado de multiplicar las dos probabilidades anteriores.
- Probabilidad Posterior: Una probabilidad ajustada que se calcula dividiendo la Probabilidad Conjunta de cada idea por la suma de todas las probabilidades conjuntas.
Galería de imágenes
-
Un letrero de neón que muestra el enunciado del teorema de Bayes
Véase también
En inglés: Bayes' theorem Facts for Kids
- Inferencia bayesiana
- Estadística bayesiana
