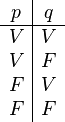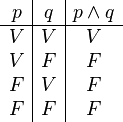Tautología para niños
Datos para niños Tautología |
||
|---|---|---|
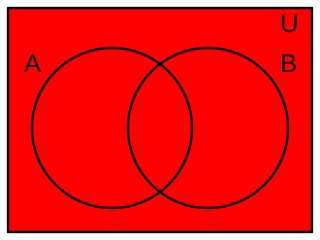 Diagrama de Venn de la conectiva
|
||
| Nomenclatura | ||
| Lenguaje formal |  |
|
| Tabla de verdad | ||
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{c|c||c} A & B & \top \ \hline V & V & V \ V & F & V \ F & V & V \ F & F & V \ \end{array} | ||
En lógica, una tautología es una afirmación o frase que siempre es verdadera. Esto ocurre sin importar cómo interpretemos sus partes. Imagina una frase que, no importa lo que pase, siempre resulta ser cierta. Por ejemplo, "Está lloviendo o no está lloviendo" es una tautología. Siempre será verdad, porque una de las dos opciones debe ser cierta.
Para saber si una frase lógica es una tautología, podemos usar una herramienta llamada tabla de verdad.
Contenido
¿Qué son las Tablas de Verdad?
Una tabla de verdad nos ayuda a analizar todas las posibles situaciones de una frase lógica. Nos muestra si la frase completa es verdadera o falsa en cada una de esas situaciones.
¿Cómo se Construye una Tabla de Verdad?
Para construir una tabla de verdad, primero identificamos las partes más pequeñas de nuestra frase. A estas partes las llamamos "fórmulas atómicas" o "proposiciones". Luego, asignamos todos los posibles valores de "verdadero" (V) o "falso" (F) a cada una de estas partes.
Por ejemplo, si tenemos la frase "p y q" (que se escribe como p ∧ q):
- p y q son nuestras proposiciones.
- Cada una puede ser V o F.
- Hay 22 = 4 combinaciones posibles para p y q.
Aquí vemos las combinaciones:
Analizando una Frase con una Tabla de Verdad
Ahora, vamos a calcular el valor de verdad de la frase completa "p y q" para cada combinación:
Como puedes ver, la frase "p y q" solo es verdadera cuando tanto p como q son verdaderas. En los otros casos, es falsa. Por lo tanto, "p y q" no es una tautología, porque no siempre es verdadera.
Un Ejemplo de Tautología
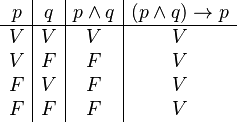
Ahora, veamos una frase que sí es una tautología: "(p y q) entonces p" (que se escribe como (p ∧ q) → p).
¡Mira la última columna! Todos los resultados son "V" (Verdadero). Esto significa que la frase "(p y q) entonces p" siempre es verdadera, sin importar los valores de p y q. ¡Es una tautología!
Si una frase tiene n proposiciones diferentes, habrá 2n combinaciones posibles. Las tablas pueden ser grandes, pero siempre nos permiten saber si una frase es una tautología o no.
Tautologías en las Reglas Lógicas
En lógica, las tautologías también se usan como "reglas de reemplazo". Esto significa que podemos usar una tautología para simplificar o cambiar una frase lógica sin alterar su significado. Ayudan a evitar la repetición en las demostraciones lógicas.
Hay dos principios importantes relacionados con esto:
- El principio de idempotencia de la disyunción: Si tienes "P o P", es lo mismo que solo "P".
: 
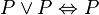
- El principio de idempotencia de la conjunción: Si tienes "P y P", es lo mismo que solo "P".
: 
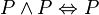Estos principios nos dicen que repetir una afirmación en una "o" o en una "y" no cambia el resultado final.
Galería de imágenes
-
Diagrama de Venn para una tautología sin variables.
-
Diagrama de Venn para una tautología con una variable.
-
Diagrama de Venn para una tautología con dos variables.
Véase también
En inglés: Tautology (logic) Facts for Kids
- Cálculo lógico
- Principio de identidad
- Verdad lógica
