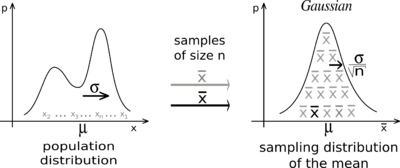Teorema del límite central para niños
El teorema central del límite es una idea muy importante en las matemáticas y la estadística. Nos dice que si sumamos muchas variables aleatorias independientes (como los resultados de muchos lanzamientos de un dado), la forma de la distribución de esa suma se parecerá mucho a una distribución normal. La distribución normal también se conoce como campana de Gauss por su forma.
Esto significa que, aunque las variables individuales no sigan una distribución normal, su suma sí lo hará, siempre que tengamos suficientes variables. Es como si, al juntar muchos elementos diferentes, el resultado final siempre tendiera a un patrón común.
El nombre de este teorema fue popularizado por el matemático George Pólya en 1920. Sin embargo, las ideas detrás de él son mucho más antiguas, ¡se remontan a 1811! Este teorema es un puente entre las matemáticas de la probabilidad antiguas y las modernas.
Por ejemplo, imagina que lanzas una moneda muchas veces y anotas cuántas veces sale cara. Si repites este experimento muchas veces y calculas el promedio de caras en cada serie de lanzamientos, el teorema central del límite nos dice que la distribución de esos promedios se parecerá a una campana de Gauss.
Este teorema tiene varias versiones. La más común es para variables que son independientes y tienen la misma distribución. Pero también hay versiones para variables que no son idénticas o no son completamente independientes, siempre que cumplan ciertas condiciones.
La versión más antigua de este teorema, que explica cómo la distribución normal puede aproximar la distribución binomial, se conoce como el teorema de De Moivre-Laplace.
Contenido
¿Qué es una variable aleatoria?
Para entender el teorema, primero necesitamos saber qué es una variable aleatoria. Una variable aleatoria es un valor que depende del resultado de un evento al azar. Por ejemplo, si lanzas un dado, el número que sale es una variable aleatoria.
Cada variable aleatoria tiene una media (el valor promedio que esperamos obtener) y una varianza (que nos dice qué tan dispersos están los valores). El teorema central del límite funciona cuando estas medias y varianzas son valores finitos (no infinitos).
¿Cómo funciona el teorema central del límite?
Imagina que tienes una serie de variables aleatorias, digamos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): X_1, X_2, \dots, X_n . Cada una de estas variables es independiente de las demás y tiene la misma media (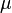 ) y varianza (
) y varianza (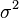 ).
).
Si sumamos estas variables para obtener Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S_n = X_1 + \cdots + X_n , el teorema nos dice que, a medida que el número de variables ( ) se hace muy grande, la distribución de
) se hace muy grande, la distribución de 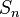 se acerca a una distribución normal.
se acerca a una distribución normal.
Para que sea más fácil de usar, a menudo se "estandariza" esta suma. Esto significa que se ajusta para que su media sea 0 y su desviación estándar sea 1. La variable estandarizada se ve así:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Z_n:=\frac{S_n-n\mu}{\sigma\sqrt{n}}
Cuando  es muy grande, la distribución de
es muy grande, la distribución de 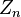 se parece mucho a la distribución normal estándar.
se parece mucho a la distribución normal estándar.
El teorema clásico
El teorema clásico del límite central se aplica cuando las variables aleatorias son independientes y tienen la misma distribución. Nos dice que la media muestral (el promedio de las muestras) se acerca a la media real de la población a medida que tomamos más y más muestras.
Más específicamente, el teorema explica cómo se comportan las pequeñas variaciones alrededor de esa media. Dice que si multiplicamos la diferencia entre la media muestral y la media real por la raíz cuadrada del número de muestras, el resultado se distribuye de forma normal.
Esto es muy útil porque no necesitamos saber cómo se distribuyen las variables individuales. El teorema nos asegura que, si tenemos suficientes datos, el promedio de esos datos se comportará de una manera predecible y conocida (la distribución normal).
Características importantes
- El teorema central del límite asegura que la distribución será aproximadamente normal cuando el número de datos (
 ) es lo suficientemente grande.
) es lo suficientemente grande. - Hay diferentes versiones del teorema, pero la más simple dice que las variables deben ser independientes, tener la misma distribución y tener una media y varianza finitas.
- La aproximación a la distribución normal es mejor en el centro de la distribución que en los extremos. Por eso se llama "central" al límite.
- Este teorema es fundamental en la teoría de probabilidad y se usa en muchos campos, como la inferencia estadística, que nos permite sacar conclusiones sobre una población a partir de una muestra.
¿Qué pasa si la varianza es nula o infinita?
El teorema central del límite funciona si la varianza de las variables es un número finito y mayor que cero. Si la varianza es nula o infinita, la distribución de la suma de las variables no se acercará a una distribución normal.
Varianza infinita
Un ejemplo de una distribución con varianza infinita es la distribución de Cauchy. Si sumamos variables que siguen una distribución de Cauchy, la suma también seguirá una distribución de Cauchy, no una normal. Esto significa que el teorema central del límite no se aplica en este caso.
Varianza nula
Si la varianza es nula, significa que todas las variables tienen exactamente el mismo valor. En este caso, la suma de las variables simplemente será ese valor multiplicado por el número de variables, y su distribución no cambiará, no se parecerá a una normal.
Galería de imágenes
Véase también
 En inglés: Central limit theorem Facts for Kids
En inglés: Central limit theorem Facts for Kids