Conjetura para niños
Una conjetura es una idea o una suposición que se cree que es cierta, pero que todavía no ha sido demostrada. Es como una hipótesis que se basa en observaciones o indicios.
En el mundo de las matemáticas, una conjetura es una afirmación que se piensa que es verdadera, pero que aún no se ha podido probar o refutar. Cuando una conjetura se demuestra que es cierta, se convierte en un teorema. Los teoremas son verdades matemáticas que ya han sido probadas y se pueden usar para demostrar otras cosas. Algunas conjeturas, como la hipótesis de Riemann o el último teorema de Fermat, han sido muy importantes en la historia de las matemáticas. Han impulsado a los matemáticos a crear nuevas áreas de estudio para poder resolverlas.
Contenido
¿Qué son las conjeturas en matemáticas?
Durante mucho tiempo, una de las conjeturas más famosas fue el último teorema de Fermat. Se le llamó "teorema" aunque no estaba demostrado. Pierre de Fermat dijo que tenía una prueba, pero nunca se encontró entre sus escritos. Esta conjetura fue un desafío para los matemáticos durante más de 300 años. Finalmente, Andrew Wiles la demostró en 1993, y entonces sí se convirtió en un teorema.
Aquí tienes algunas de las conjeturas más conocidas:
- No existen números perfectos impares.
- Conjetura de Goldbach
- Conjetura de los números primos gemelos
- Conjetura de Collatz
- Hipótesis de Riemann
- P ≠ NP
- Conjetura de Poincaré (demostrada por Grigori Perelmán)
- Conjetura abc
El Último Teorema de Fermat: Un Gran Desafío
En la teoría de números, el último teorema de Fermat dice que no hay tres números enteros positivos (llamémoslos a, b y c) que puedan cumplir la ecuación a^n + b^n = c^n si el número n es mayor que dos.
Pierre de Fermat propuso esta idea en 1637. La escribió en el margen de un libro, diciendo que tenía una prueba, pero que era demasiado larga para caber allí. Después de 358 años de intentos por parte de muchos matemáticos, Andrew Wiles presentó la primera prueba exitosa en 1994, y se publicó en 1995. Este problema sin resolver impulsó el desarrollo de la teoría algebraica de números en el siglo XIX. Es uno de los teoremas más importantes en la historia de las matemáticas. Antes de ser demostrado, estuvo en el Libro Guinness de los Récords Mundiales como uno de los "problemas matemáticos más difíciles".
El Teorema de los Cuatro Colores: Coloreando Mapas
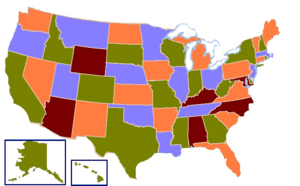
El teorema de los cuatro colores dice que, si tienes un mapa con regiones que se tocan, solo necesitas cuatro colores para pintar todas las regiones. La regla es que dos regiones que se tocan no pueden tener el mismo color. Dos regiones se tocan si comparten una línea, no solo una esquina. Por ejemplo, en el mapa de los Estados Unidos, Utah y Arizona se tocan, pero Utah y Nuevo México no, porque solo comparten un punto.
La idea de este problema surgió en 1852, cuando Francis Guthrie intentaba colorear un mapa de Inglaterra y notó que solo necesitaba cuatro colores. A finales del siglo XIX, se demostró el teorema de los cinco colores, que es más sencillo. Pero probar que cuatro colores eran suficientes fue mucho más difícil. Hubo muchas pruebas falsas y ejemplos que parecían refutarlo.
Finalmente, el teorema de los cuatro colores fue demostrado en 1976 por Kenneth Appel y Wolfgang Haken. Fue el primer teorema importante que se demostró usando una computadora. Ellos mostraron que había un grupo de 1936 mapas que no podían ser parte de un contraejemplo. Usaron un programa de computadora para verificar esto. Aunque al principio la prueba asistida por computadora generó dudas, con el tiempo ha sido más aceptada.
La Conjetura de Poincaré: Formas en el Espacio
La conjetura de Poincaré es un teorema sobre cómo se puede describir la 3-esfera. La 3-esfera es como la superficie de una pelota, pero en cuatro dimensiones. La conjetura dice que:
La esfera de cuatro dimensiones, también llamada 3-esfera o hiperesfera, es la única forma compacta de cuatro dimensiones donde cualquier lazo o círculo cerrado se puede encoger hasta un punto. Esto significa que solo hay una forma cerrada y "simplemente conexa" (sin agujeros) de tres dimensiones: la esfera de cuatro dimensiones.
Henri Poincaré propuso esta conjetura. Se refiere a un espacio que, de cerca, parece un espacio tridimensional normal, pero está conectado, tiene un tamaño finito y no tiene bordes. La conjetura de Poincaré afirma que si un espacio así tiene la propiedad de que cada bucle se puede encoger a un punto, entonces debe ser una esfera tridimensional.
Después de casi un siglo de trabajo de muchos matemáticos, Grigori Perelman presentó una prueba de la conjetura en 2002 y 2003. Su prueba se basó en el trabajo de Richard S. Hamilton. Varios equipos de matemáticos han confirmado que la prueba de Perelman es correcta. Antes de ser probada, la conjetura de Poincaré era uno de los problemas más importantes sin resolver en topología.
El Problema P versus NP: ¿Qué tan Rápido es un Ordenador?
El problema P versus NP es un gran problema sin resolver en informática. En pocas palabras, se pregunta si cualquier problema cuya solución puede ser verificada rápidamente por un ordenador, también puede ser resuelto rápidamente por un ordenador. La mayoría de los expertos creen que la respuesta es no.
Este problema fue mencionado por primera vez en 1956 por Kurt Gödel. La forma precisa del problema P=NP fue presentada en 1971 por Stephen Cook. Muchos lo consideran el problema abierto más importante en este campo. Es uno de los siete Problemas del milenio elegidos por el Instituto Clay de Matemáticas. Ofrecen un premio de un millón de dólares a quien encuentre la primera solución correcta.
¿Cómo se resuelven las conjeturas?
La Demostración: Convirtiendo una Conjetura en Teorema
Las matemáticas se basan en verdades que se pueden demostrar. En matemáticas, no importa cuántos ejemplos apoyen una conjetura; si no hay una prueba lógica, no es suficiente para decir que es verdad. Un solo ejemplo que demuestre que es falsa (un "contraejemplo") puede echar abajo toda la conjetura.
A veces, las revistas de matemáticas publican resultados de investigaciones que han buscado contraejemplos más allá de lo que se había hecho antes. Por ejemplo, la conjetura de Collatz ha sido probada para números muy grandes (más de un billón). Sin embargo, no encontrar un contraejemplo después de una búsqueda extensa no prueba que la conjetura sea verdadera. Podría ser falsa, pero con un contraejemplo muy, muy grande.
Los matemáticos a menudo creen que una conjetura es muy probable que sea cierta, incluso si aún no está probada. Esto puede ser porque sus consecuencias se han verificado o porque está muy relacionada con otros resultados conocidos.
Una conjetura se considera probada solo cuando se ha demostrado que es imposible que sea falsa. Hay varios métodos para hacer esto, que se estudian en las demostraciones matemáticas.
Un método de prueba, cuando solo hay un número limitado de casos que podrían ser contraejemplos, se llama "fuerza bruta". En este método, se revisan todos los casos posibles y se demuestra que ninguno es un contraejemplo. A veces, el número de casos es tan grande que se necesita una computadora para verificar todos. Por ejemplo, las pruebas por computadora del teorema de los cuatro colores en 1976 y 1997 fueron dudosas al principio, pero luego se confirmaron.
Cuando una conjetura ha sido demostrada, deja de ser una conjetura y se convierte en un teorema. Muchos teoremas importantes fueron conjeturas en el pasado, como el teorema de geometrización (que resolvió la conjetura de Poincaré) y el último teorema de Fermat.
La Refutación: Cuando una Conjetura es Falsa
Las conjeturas que se demuestran falsas con un contraejemplo a veces se llaman "conjeturas falsas". Un ejemplo es la conjetura de la suma de potencias de Euler. El primer contraejemplo encontrado para esta conjetura involucraba números muy grandes, aunque luego se encontró uno más pequeño.
Conjeturas Independientes: Ni Verdaderas Ni Falsas
No todas las conjeturas terminan siendo verdaderas o falsas. La hipótesis del continuo, que trata sobre el tamaño de ciertos conjuntos infinitos, se demostró que es independiente de los axiomas de la teoría de conjuntos que se usan normalmente. Esto significa que se puede aceptar esta afirmación o su negación como un nuevo axioma sin que haya contradicciones.
En estos casos, si una prueba usa una de estas afirmaciones, los investigadores a menudo buscan una nueva prueba que no la necesite. La única excepción importante es el axioma de elección, que muchos investigadores usan sin preocuparse si un resultado lo requiere.
Demostraciones Condicionales: Usando Conjeturas como Base
A veces, una conjetura se llama "hipótesis" cuando se usa mucho como una suposición para demostrar otros resultados. Por ejemplo, la hipótesis de Riemann es una conjetura que predice cómo se distribuyen los números primos. Pocos matemáticos dudan de que la hipótesis de Riemann sea cierta. De hecho, algunos han desarrollado otras pruebas que dependen de que esta conjetura sea verdad. A estas se les llama "demostraciones condicionales": las conjeturas que se asumen aparecen en las condiciones del teorema, por el momento.
Sin embargo, estas "demostraciones" dejarían de ser válidas si la hipótesis resultara ser falsa. Por eso, hay mucho interés en verificar si estas conjeturas son verdaderas o falsas.
Véase también
 En inglés: Conjecture Facts for Kids
En inglés: Conjecture Facts for Kids
- Lista de conjeturas matemáticas
- Hipótesis
- Experimento mental