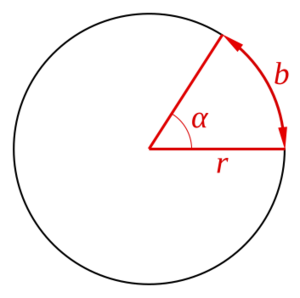robot de la enciclopedia para niños

Radián para niños

Enciclopedia para niños

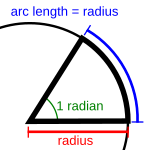
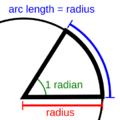
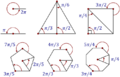
El radián (símbolo: rad) es una unidad especial que usamos para medir la amplitud de los ángulos. Imagina un círculo: un radián mide un ángulo que tiene su vértice en el centro del círculo. La característica principal de este ángulo es que el arco de la circunferencia que abarca tiene la misma longitud que el radio del círculo. Es como si el radio "se doblara" para formar el arco.

Hasta 1995, el radián era una unidad "suplementaria" en el Sistema Internacional de Unidades, junto con el estereorradián. Después de ese año, se clasificó como una unidad derivada. El radián se considera una unidad sin dimensiones, lo que significa que no tiene una unidad física como metros o segundos.

Esta unidad es muy importante y se usa mucho en física, cálculo infinitesimal, trigonometría y otras áreas de las matemáticas.

Archivo:Radian measure-def2
Un ángulo de 1 radián corresponde al arco de circunferencia cuya longitud es su radio. Una circunferencia completa corresponde a 2π radianes.

¿Qué es un radián?

Un radián es la medida de un ángulo que se forma en el centro de un círculo. Los lados de este ángulo cortan la circunferencia, y la parte de la circunferencia que queda entre esos lados (llamada arco) mide exactamente lo mismo que el radio del círculo.

Archivo:Radian cropped color
Un radián es el ángulo donde el arco es igual al radio.

Para calcular un ángulo en radianes, dividimos la longitud del arco (s) entre la longitud del radio (r). La fórmula es: θ = s/r. Aquí, θ (la letra griega "theta") representa el ángulo en radianes.

Por ejemplo, si queremos saber cuántos radianes tiene un círculo completo, sabemos que la longitud de toda la circunferencia es 2π veces el radio (2πr). Si dividimos esto entre el radio (r), obtenemos: 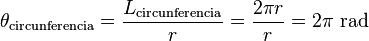\theta_\text{circunferencia}=\frac {L_\text{circunferencia}}{r} =\frac {2 \pi r}{r}=2 \pi\ \text{rad}\, Esto significa que un círculo completo tiene 2π radianes. Un ángulo recto (90°) es exactamente π/2 radianes.

¿Para qué sirve el radián?

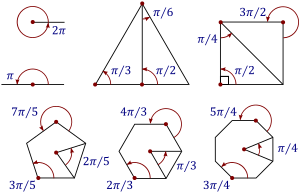
El radián es una unidad muy útil para medir ángulos porque simplifica muchos cálculos en matemáticas y física. Los ángulos más comunes se pueden expresar con números sencillos que incluyen π (pi).

Símbolo del radián

El símbolo oficial para el radián es rad. Así lo establecen la Oficina Internacional de Pesas y Medidas y la Organización Internacional de Normalización. Antes se usaban otros símbolos como c o R, pero ya no son comunes para evitar confusiones.

Por ejemplo, un ángulo de 1.2 radianes se escribe como 1.2 rad. En muchos textos de matemáticas, el símbolo "rad" a menudo se omite. Si ves un número sin el símbolo de grado (°) al lado, se asume que el ángulo está en radianes.

Equivalencias importantes

La relación más importante es entre grados sexagesimales y radianes:

  • π rad = 180°

Esto significa que:

  • 1 radián es aproximadamente 57.29577951 grados (180/π).
  • 1 grado sexagesimal es aproximadamente 0.01745329252 radianes (π/180).

También existe una equivalencia con los grados centesimales:

  • π rad = 200g

La siguiente tabla muestra la conversión de algunos ángulos comunes:

Conversión de ángulos comunes
Revolución Radian Grado
sexagesimal		 Gradián Miliradián Puntos del compás
0 de circulo 0 rad 0° 0g 0 mrad 0 pt
1/72 de circulo π/36 rad 𝜏/72 rad  ≈ 0,08727 rad 5° 50/9g 250π/9 mrad 125𝜏/9 mrad ≈ 87,266 mrad 4/9 pt
1/24 de circulo π/12 rad 𝜏/24 rad ≈ 0,2618 rad 15° 50/3g 250π/3 mrad 125𝜏/3 mrad ≈ 261,799 mrad 4/3 pt
1/16 de circulo π/8 rad 𝜏/16 rad ≈ 0,3927 rad 22,5° o 22°30′ 25g 125π mrad 125𝜏/2 mrad ≈ 392,699 mrad 2 pt
1/12 de circulo π/6 rad 𝜏/12 rad ≈ 0,5236 rad 30° 100/3g 500π/3 mrad 250𝜏/3 mrad ≈ 523,599 mrad 8/3 pt
1/10 de circulo π/5 rad 𝜏/10 rad ≈ 0,6283 rad 36° 40g 200π mrad 100𝜏 mrad ≈ 628,319 mrad 16/5 pt
1/8 de circulo π/4 rad 𝜏/8 rad ≈ 0,7854 rad 45° 50g 250π mrad 125𝜏 mrad ≈ 785,398 mrad 4 pt
1/2π de circulo 1 rad 180/π° 200/πg 1000 mrad 16/π pt
1/6 de circulo π/3 rad 𝜏/6 rad ≈ 1,047 rad 60° 200/3g 1000π/3 mrad 500𝜏/3 mrad ≈ 1047,198 mrad 16/3 pt
1/5 de circulo 2π/5 rad 𝜏/5 rad ≈ 1,257 rad 72° 80g 400π mrad 200𝜏 mrad ≈ 1256,637 mrad 32/5 pt
1/4 de circulo π/2 rad 𝜏/4 rad ≈ 1,571 rad 90° 100g 500π mrad 250𝜏 mrad ≈ 1570,796 mrad 8 pt
1/3 de circulo 2π/3 rad 𝜏/3 rad ≈ 2,094 rad 120° 400/3g 2000π/3 mrad 1000𝜏/3 mrad ≈ 2094,395 mrad 32/3 pt
2/5 de circulo 4π/5 rad 2𝜏/5 rad ≈ 2,513 rad 144° 160g 800π mrad 400𝜏 mrad ≈ 2513,274 mrad 64/5 pt
1/2 de circulo π rad 𝜏/2 rad ≈ 3,142 rad 180° 200g 1000π mrad 500𝜏 mrad ≈ 3141,593 mrad 16 pt
3/4 de circulo 3π/2 rad 3𝜏/4 rad ≈ 4,712 rad 270° 300g 1500π mrad 750𝜏 mrad ≈ 4712,389 mrad 24 pt
1 circulo 2π rad 𝜏 rad ≈ 6,283 rad 360° 400g 2000π mrad 1000𝜏 mrad ≈ 6283,185 mrad 32 pt


Otras unidades para medir ángulos son el grado sexagesimal, el grado centesimal y, en astronomía, la hora.

El radián también se usa para medir la velocidad angular, que es qué tan rápido gira algo. La unidad para esto es el radián por segundo (rad/s).

Cómo convertir entre grados y radianes

Los grados y los radianes son dos formas diferentes de medir ángulos. Recuerda que un círculo completo (360°) equivale a 2π radianes.

Convertir grados a radianes

Para convertir un ángulo de grados a radianes, usamos la relación que 180° es igual a π radianes.

Por ejemplo, para convertir 137° a radianes: Sabemos que 1° = π/180 radianes. Entonces, multiplicamos 137° por (π/180): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 137^\circ \cdot \frac{\pi}{180^\circ} = \frac{137\pi}{180} Así, 137° es igual a 137π/180 radianes.

Convertir radianes a grados

Para convertir un ángulo de radianes a grados, usamos la misma relación, pero al revés. Multiplicamos la medida en radianes por (180°/π).

Por ejemplo, para convertir 137π/180 radianes a grados: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{137\pi}{180} \cdot \frac{180^\circ}{\pi} = \frac{24660^\circ}{180} = 137^\circ El resultado es 137°.

Archivo:Radian-common
Ángulos de los polígonos más comunes medidos en radianes, expresados como fracciones de π
Archivo:Degree-Radian Conversion
Tabla de conversión entre grados sexagesimales y radianes

Radián, gradián y grado sexagesimal: ¿Cuál es la diferencia?

Estas tres son unidades para medir ángulos planos, y se distinguen así:

  • Radián (rad): Es el ángulo que abarca un arco cuya longitud es igual a la del radio del círculo.
  • Gradián o grado centesimal (g): Es el ángulo que abarca un arco que mide la 1/400 parte de una circunferencia completa.
  • Grado sexagesimal (°): Es el ángulo que abarca un arco que mide la 1/360 parte de una circunferencia completa.

Conversión de ángulos comunes

Unidades Valores
Revolución   0 1/72 1/12 1/8 1/6 1/4 1/2 3/4 1
Grados (sexagesimales)   0° 5° 30° 45° 60° 90° 180° 270° 360°
Radianes 0 rad π/36 rad π/6 rad π/4 rad π/3 rad π/2 rad π rad 3π/2 rad 2π rad
𝜏/72 rad 𝜏/12 rad 𝜏/8 rad 𝜏/6 rad 𝜏/4 rad 𝜏/2 rad 3𝜏/4 rad 𝜏 rad
Gradianes (grados centesimales) 0g 50g/9 100g/3 50g 200g/3 100g 200g 300g 400g

Galería de imágenes

  • Radian measure-def2

    Un ángulo de 1 radián corresponde al arco de circunferencia cuya longitud es su radio. Una circunferencia completa corresponde a 2π radianes.

  • Radian cropped color

    Un radián es el ángulo donde el arco es igual al radio.

  • Radian-common

    Ángulos de los polígonos más comunes medidos en radianes, expresados como fracciones de π

  • Degree-Radian Conversion

    Tabla de conversión entre grados sexagesimales y radianes

Ver también

Véase también

Kids robot.svg En inglés: Radian Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Radián&oldid=4897232»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Radián para Niños. Enciclopedia Kiddle.