robot de la enciclopedia para niños

Unidad imaginaria para niños

Enciclopedia para niños


Archivo:ImaginaryUnit5
i en el plano complejo o de Argand. Los números reales se encuentran en el eje horizontal y los números imaginarios en el eje vertical.

La unidad imaginaria es un número especial en matemáticas que se representa con la letra i. Este número es muy importante porque nos ayuda a resolver problemas que no se pueden solucionar solo con los números que usamos normalmente (los números reales).

La característica principal de la unidad imaginaria es que, cuando la multiplicas por sí misma (la elevas al cuadrado), el resultado es -1. Esto se escribe así: 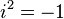i^2 = -1.

Aunque no existe un número real que, al multiplicarse por sí mismo, dé un resultado negativo, la unidad imaginaria nos permite crear un nuevo tipo de números llamados números complejos. Estos números combinan una parte real y una parte imaginaria, como por ejemplo, 2+3i.

Los números imaginarios son muy útiles porque amplían el mundo de las matemáticas. Gracias a ellos, podemos encontrar soluciones para ecuaciones que antes no tenían respuesta en el conjunto de los números reales.

Existen dos números complejos que, al elevarse al cuadrado, dan -1: son i y -i.

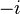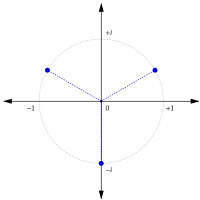
En algunos campos, como la ingeniería eléctrica, la unidad imaginaria se representa con la letra j en lugar de i. Esto se hace para evitar confusiones, ya que la letra i se usa comúnmente para representar la corriente eléctrica.

¿Qué es la unidad imaginaria?

Las potencias de i

siguen un patrón:
... (El patrón se repite)
i−3 = i
i−2 = −1
i−1 = −i
i0 = 1
i1 = i
i2 = −1
i3 = −i
i4 = 1
i5 = i
i6 = −1
... (El patrón se repite)

La unidad imaginaria i se define por una única propiedad: su cuadrado es -1. Esto significa que: i^2=-1

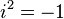
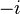A partir de esta definición, podemos ver que tanto i como -i son las raíces cuadradas de -1.

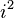Aunque se le llama "imaginaria", esta construcción es completamente válida en matemáticas. Podemos realizar operaciones con números imaginarios y complejos de la misma manera que con números reales. Simplemente tratamos a i como una cantidad desconocida y, cada vez que aparece i^2, lo reemplazamos por -1.

Las potencias más altas de i también siguen un patrón:

  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i^3 = i^2 \cdot i = (-1) \cdot i = -i
  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i^4 = i^3 \cdot i = (-i) \cdot i = -(i^2) = -(-1) = 1
  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i^5 = i^4 \cdot i = (1) \cdot i = i

Este patrón se repite cada cuatro potencias.

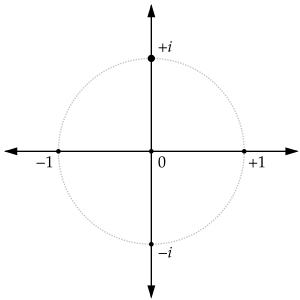
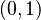En el plano complejo, que es como un plano cartesiano especial, i se representa como el punto (0,1). Esto significa que está a una unidad de distancia del origen, sobre el eje que representa los números imaginarios.

¿Por qué hay dos soluciones, i y -i?

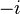La ecuación x^2=-1 tiene dos soluciones diferentes: i y -i. Ambas son igualmente válidas. Una vez que elegimos una de ellas para llamarla i, la otra se convierte automáticamente en -i.

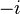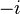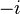No hay una diferencia matemática fundamental entre i y -i. Ambas son "opuestas" entre sí, pero ambas cumplen la condición de que su cuadrado es -1. La elección de cuál es i y cuál es -i es solo una forma de nombrarlas.

Cuidado al usar la unidad imaginaria

A veces, la unidad imaginaria se escribe como \sqrt{-1}. Sin embargo, hay que tener mucho cuidado al usar esta notación, especialmente con las reglas de las raíces cuadradas. Las reglas que usamos para las raíces de números reales positivos no siempre funcionan igual con los números imaginarios.

Por ejemplo, si no tenemos cuidado, podríamos cometer un error como este: 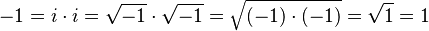-1 = i \cdot i = \sqrt{-1} \cdot \sqrt{-1} = \sqrt{(-1) \cdot (-1)} = \sqrt{1} = 1 (¡Esto es incorrecto!)

Las reglas de multiplicación y división de raíces, como 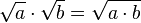\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}, solo son válidas cuando los números a y b son reales y no negativos.

Propiedades de la unidad imaginaria

Raíces cuadradas de i

Archivo:Imaginary2Root
Las dos raíces cuadradas de i en el plano complejo
Archivo:Imaginary3Root
Las tres raíces cúbicas de i en el plano complejo

El número i tiene dos raíces cuadradas, al igual que la mayoría de los números complejos (excepto el cero). Estas dos raíces se pueden encontrar resolviendo la ecuación Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 = i .

Las raíces cuadradas de i son: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \pm \left( \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i \right)

Si elevamos al cuadrado cualquiera de estas expresiones, obtenemos i.

Raíces cúbicas de i

Las tres raíces cúbicas de i son:

  • -i
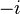
  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\sqrt{3}}{2} + \frac{i}{2}
  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -\frac{\sqrt{3}}{2} + \frac{i}{2}

Estas raíces, al igual que las raíces de 1, forman los vértices de polígonos regulares si los dibujamos en el plano complejo.

Multiplicación y división por i

Multiplicar un número complejo por i es como girarlo 90 grados en sentido contrario a las agujas del reloj en el plano complejo. Por ejemplo, si tienes un número complejo a+bi:

  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i \cdot (a+bi) = ai + bi^2 = ai - b = -b+ai

Dividir por i es lo mismo que multiplicar por -i.

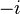  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{i} = \frac{1}{i} \cdot \frac{i}{i} = \frac{i}{i^2} = \frac{i}{-1} = -i

Entonces, dividir un número complejo por i es como girarlo 90 grados en el sentido de las agujas del reloj:

  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a+bi}{i} = (a+bi) \cdot (-i) = -ai - bi^2 = -ai + b = b-ai

Potencias de i

Las potencias de i se repiten en un ciclo de cuatro valores:

  • i^1 = i
  • i^2 = -1
  • i^3 = -i
  • i^4 = 1
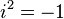
  • i^5 = i (el ciclo se repite)

Para saber el valor de i elevado a cualquier número entero n, solo tienes que dividir n entre 4 y ver el resto. El resultado será el mismo que i elevado a ese resto. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i^{25} es igual a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i^1 porque 25 dividido por 4 da un resto de 1.

i elevado a la i

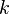Una curiosidad matemática es el valor de i elevado a la i. Usando una fórmula especial llamada fórmula de Euler, se puede demostrar que: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i^i = e^{- (\pi/2 + 2k \pi)} donde k es cualquier número entero. El valor principal (cuando k=0) es aproximadamente Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0.207879576... , que es un número real.

Factorial de i

El factorial de la unidad imaginaria i se calcula usando una función matemática llamada función gamma. Su valor aproximado es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i! = \Gamma(1+i) \approx 0.4980 - 0.1549i

Otras operaciones

Muchas operaciones matemáticas que conoces para los números reales también se pueden hacer con i y los números complejos. Esto incluye elevar a potencias, sacar raíces, usar logaritmos y funciones trigonométricas.

Por ejemplo:

  • El coseno de i es un número real:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos(i) = \cosh(1) \approx 1.543

  • El seno de i es un número puramente imaginario:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin(i) = i \sinh(1) \approx 1.175i

Nombres alternativos

  • En ingeniería eléctrica y campos relacionados, la unidad imaginaria se suele escribir como j. Esto es para evitar confundirla con la letra i que se usa para la corriente eléctrica.
  • Algunos textos usan la letra griega iota (ι) para la unidad imaginaria, especialmente para evitar confusiones con índices.

Véase también

Kids robot.svg En inglés: Imaginary unit Facts for Kids

  • Multiplicidad (matemáticas)
  • Raíz de unidad
  • Unidad número complejo

Galería de imágenes

  • ImaginaryUnit5

    i en el plano complejo o de Argand. Los números reales se encuentran en el eje horizontal y los números imaginarios en el eje vertical.

  • Imaginary2Root

    Las dos raíces cuadradas de i en el plano complejo

  • Imaginary3Root

    Las tres raíces de cubo de i en el plano complejo

Obtenido de «https://ninos.kiddle.co/index.php?title=Unidad_imaginaria&oldid=5051523»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Unidad imaginaria para Niños. Enciclopedia Kiddle.