Fórmula de De Moivre para niños
La fórmula de De Moivre es una regla matemática muy útil que conecta los números complejos con la trigonometría. Fue nombrada en honor al matemático Abraham de Moivre.
Esta fórmula dice que para cualquier número real x y para cualquier número entero n, se cumple lo siguiente:
 .
.
Aquí, i representa la unidad imaginaria, que es la base de los números complejos. La expresión 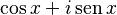 a veces se escribe de forma más corta como
a veces se escribe de forma más corta como 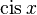 .
.
Al usar esta fórmula, podemos encontrar maneras de calcular 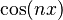 y
y 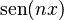 usando
usando 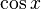 y
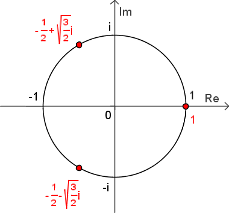
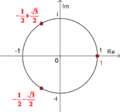
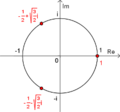
y 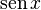 . También nos ayuda a encontrar las raíces de la unidad, que son números complejos que, al elevarlos a una potencia n, dan como resultado 1.
. También nos ayuda a encontrar las raíces de la unidad, que son números complejos que, al elevarlos a una potencia n, dan como resultado 1.
Contenido
Historia de la Fórmula de De Moivre
La idea detrás de la fórmula de De Moivre apareció por primera vez en los trabajos del matemático Abraham de Moivre alrededor de 1707. Él la usó para entender las raíces de los números complejos.
Más tarde, en 1748, el famoso matemático Leonhard Euler presentó la fórmula en su libro Introductio in analysin infinitorum de la forma en que la conocemos hoy. Euler demostró que la fórmula funciona para todos los números enteros positivos.

Conexión con la Fórmula de Euler
La fórmula de De Moivre está muy relacionada con otra fórmula importante en matemáticas, la fórmula de Euler. Esta fórmula dice que:
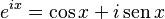
Si elevamos ambos lados de la fórmula de Euler a la potencia n, obtenemos:
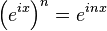
Y si aplicamos la fórmula de Euler de nuevo al lado derecho, vemos que:
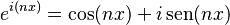 .
.
Así, la fórmula de De Moivre se puede entender como una consecuencia de la fórmula de Euler.
La Identidad de Euler
Un resultado muy interesante que se obtiene de la fórmula de Euler es la identidad de Euler. Si en la fórmula de Euler (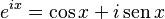 ) sustituimos x por el número pi (
) sustituimos x por el número pi ( ), obtenemos:
), obtenemos:
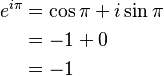
Esto nos da la famosa identidad:

Esta identidad es considerada una de las más bellas en matemáticas porque conecta cinco números fundamentales: e, i,  , 1 y 0.
, 1 y 0.
¿Para qué se usa la Fórmula de De Moivre?
La fórmula de De Moivre es muy útil para trabajar con números complejos, especialmente cuando están escritos en su forma polar. Un número complejo en forma polar se ve así:
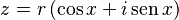
Aquí, r es la distancia del número al origen en el plano complejo (llamado módulo), y x es el ángulo que forma con el eje positivo.
Calcular potencias de números complejos
Para elevar un número complejo a una potencia n, usamos la fórmula de De Moivre de esta manera:
![z^n=\left[|z|\left(\cos(x)+i\sen(x)\right)\right]^n=|z|^n\left[\cos(nx)+i\sen(nx)\right]](/images/math/f/a/d/fad3b17f2ade088806cb4182ec28625f.png)
Esto significa que para elevar un número complejo a una potencia, elevamos su módulo a esa potencia y multiplicamos su ángulo por esa misma potencia.
Encontrar raíces de números complejos
La fórmula también nos permite encontrar las n raíces de un número complejo. Esto es, encontrar los números que, al elevarlos a la potencia n, nos dan el número original. La fórmula para esto es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z^{1/n}=\left[r\left(\cos x+i\sen x\right)\right]^{1/n}=r^{1/n}\left[\cos\left( \frac{x+2k\pi}{n}\right)+i\sen\left(\frac{x+2k\pi}{n}\right)\right]
En esta fórmula, k es un número entero que va desde 0 hasta n-1. Al cambiar el valor de k, obtenemos las n raíces diferentes del número complejo z.
Galería de imágenes
Véase también
 En inglés: De Moivre's formula Facts for Kids
En inglés: De Moivre's formula Facts for Kids
- Fórmula de Euler
- Raíz de la unidad
- Números imaginarios