Teoría de cuerpos para niños

La teoría de cuerpos es una parte de las matemáticas que estudia las propiedades de los cuerpos. En matemáticas, un "cuerpo" es un conjunto de números donde puedes sumar, restar, multiplicar y dividir (excepto por cero) de una manera que siempre funciona y sigue ciertas reglas. Piensa en ellos como sistemas numéricos especiales donde estas operaciones básicas están "bien definidas".

Los cuerpos más conocidos son los números racionales (fracciones), los números reales (todos los números que conoces, incluyendo decimales) y los números complejos (números que incluyen la unidad imaginaria i). Otros cuerpos, como los cuerpos de funciones o los cuerpos de números algebraicos, se usan en áreas más avanzadas de las matemáticas, como la teoría de números y la geometría algebraica. Incluso, muchos sistemas de seguridad en internet (como los protocolos criptográficos) usan cuerpos finitos, que son cuerpos con un número limitado de elementos.

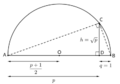
La relación entre diferentes cuerpos se estudia con la idea de "extensión de cuerpos". La teoría de Galois, creada por Évariste Galois en el siglo XIX, nos ayuda a entender las simetrías de estas extensiones. Gracias a esta teoría, sabemos que algunos problemas antiguos, como dividir un ángulo en tres partes iguales o construir un cuadrado con la misma área que un círculo usando solo regla y compás, son imposibles de resolver de esa manera. También muestra que no siempre hay una fórmula sencilla para resolver ecuaciones muy complicadas.

Los cuerpos son muy importantes en varias ramas de las matemáticas. Por ejemplo, en el análisis matemático, que estudia funciones y límites, las propiedades de los números reales son fundamentales. Además, cualquier cuerpo puede usarse para definir espacios vectoriales, que son la base del álgebra lineal, una herramienta clave en muchas ciencias. Los cuerpos de números se estudian a fondo en la teoría de números, y los cuerpos de funciones ayudan a describir formas geométricas.

¿Qué es un Cuerpo Matemático?

Un "cuerpo" en matemáticas es como un club especial de números. En este club, puedes hacer cuatro cosas principales: sumar, restar, multiplicar y dividir (¡pero nunca por cero!). Lo más importante es que estas operaciones siempre funcionan dentro del club y siguen reglas muy específicas, como las que ya conoces para los números normales.

Reglas de un Cuerpo

Imagina que tienes un conjunto de elementos (números) y dos operaciones: suma (+) y multiplicación (⋅). Para que este conjunto sea un cuerpo, debe cumplir estas reglas:

• Asociatividad: No importa cómo agrupes los números al sumar o multiplicar. Por ejemplo, (a + b) + c es lo mismo que a + (b + c).
• Conmutatividad: El orden de los números no cambia el resultado al sumar o multiplicar. Por ejemplo, a + b es lo mismo que b + a.
• Elementos Neutros: Hay un número "cero" (0) que no cambia nada al sumar (a + 0 = a), y un número "uno" (1) que no cambia nada al multiplicar (a ⋅ 1 = a). Además, 0 y 1 deben ser diferentes.
• Inversos Aditivos: Para cada número "a", hay otro número "-a" que, al sumarlo, da cero (a + (-a) = 0). Piensa en el 5 y el -5.
• Inversos Multiplicativos: Para cada número "a" que no sea cero, hay otro número "a⁻¹" que, al multiplicarlo, da uno (a ⋅ a⁻¹ = 1). Piensa en el 2 y el 1/2.
• Distributividad: La multiplicación se "distribuye" sobre la suma. Por ejemplo, a ⋅ (b + c) es lo mismo que (a ⋅ b) + (a ⋅ c).

Si un conjunto de números con estas dos operaciones cumple todas estas reglas, ¡entonces es un cuerpo!

Historia de los Cuerpos Matemáticos

La idea de los cuerpos no apareció de repente. Los matemáticos la usaron sin darle un nombre específico al principio.

• Niels Henrik Abel y Évariste Galois usaron estas ideas en el siglo XIX para resolver ecuaciones complicadas.
• En 1871, Richard Dedekind fue el primero en usar la palabra "cuerpo" para describir conjuntos de números que se comportan bien con las cuatro operaciones básicas.
• Más tarde, en 1893, Heinrich Martin Weber dio una definición más clara y formal de lo que es un cuerpo.
• Ernst Steinitz publicó un trabajo muy importante en 1910 que estudió los cuerpos de forma más profunda y definió conceptos clave que usamos hoy.
• Aunque Galois no usó el término "cuerpo", se le reconoce por ser el primero en conectar la teoría de grupos con estas ideas, lo que llevó a la famosa teoría de Galois.

Ejemplos Famosos de Cuerpos

Números Racionales (Fracciones)

Los números racionales son los que puedes escribir como una fracción (por ejemplo, 1/2, 3/4, -7/5). Aquí, el número de abajo (el denominador) no puede ser cero.

• Puedes sumar y restar fracciones.
• Puedes multiplicar fracciones.
• Puedes dividir fracciones (multiplicando por el inverso).
• Cada fracción tiene un inverso aditivo (por ejemplo, el inverso de 3/4 es -3/4).
• Cada fracción (excepto el cero) tiene un inverso multiplicativo (por ejemplo, el inverso de 3/4 es 4/3).

Por eso, los números racionales forman un cuerpo.

Números Reales (Todos los Números de la Recta)

La recta numérica representa todos los números reales.

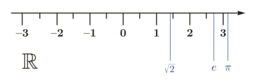
Los números reales son todos los números que puedes imaginar en una línea recta, incluyendo los números racionales (fracciones), los números enteros (como 1, 2, -3) y los números irracionales (como pi o la raíz cuadrada de 2). Con las operaciones normales de suma y multiplicación, los números reales también forman un cuerpo. Son la base de muchas áreas de las matemáticas y las ciencias.

Números Complejos (Con la Unidad Imaginaria)

La multiplicación de números complejos puede verse como giros y cambios de tamaño en un plano.

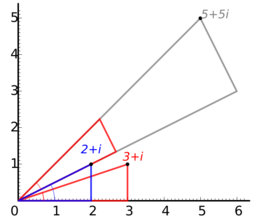
Los números complejos son un tipo de número que se escribe como a + bi, donde a y b son números reales, e i es la unidad imaginaria. La característica especial de i es que i² = -1. Aunque parezcan extraños, los números complejos también forman un cuerpo con sus propias reglas de suma y multiplicación. Se usan mucho en física, ingeniería y otras ciencias. Geométricamente, puedes pensar en ellos como puntos en un plano, donde la suma es como combinar flechas y la multiplicación es como girar y estirar esas flechas.

Un Cuerpo con Cuatro Elementos

Además de los números que ya conoces, existen cuerpos con un número limitado de elementos. Por ejemplo, hay un cuerpo con solo cuatro elementos: O, I, A y B. En este cuerpo, O es como el cero y I es como el uno. Las tablas de la derecha muestran cómo se suman y multiplican estos elementos.

Este tipo de cuerpos se llaman cuerpos finitos. El subconjunto formado por O e I (resaltado en azul en las tablas) es también un cuerpo, conocido como el cuerpo binario. En la informática, O e I a menudo representan "falso" y "verdadero", y la suma es como la operación lógica XOR. Esto significa que los cuerpos binarios son la base para trabajar con bits en las computadoras.

Aplicaciones de la Teoría de Cuerpos

La teoría de cuerpos es muy útil en diferentes áreas:

• Álgebra Lineal: Los cuerpos se usan para definir vectores y matrices. Estas son herramientas fundamentales para resolver sistemas de ecuaciones y entender transformaciones en el espacio.
• Criptografía: Los cuerpos finitos son esenciales para crear códigos seguros y proteger la información en internet. Muchos sistemas de seguridad se basan en las propiedades de estos cuerpos.
• Teoría de Números: Los cuerpos ayudan a estudiar las propiedades de los números y sus relaciones.
• Ciencias de la Computación: Los cuerpos binarios (con solo dos elementos) son la base de cómo funcionan las computadoras y la lógica digital.

Galería de imágenes

• 

  El teorema de la media geométrica muestra cómo construir la raíz cuadrada de un número usando regla y compás.

Véase también

En inglés: Field (mathematics) Facts for Kids