Sólidos arquimedianos para niños

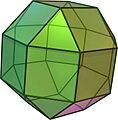
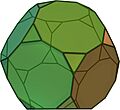
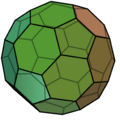
Los sólidos arquimedianos son un grupo especial de 13 figuras geométricas tridimensionales. Son poliedros, lo que significa que tienen caras planas. Lo interesante de estos sólidos es que sus caras están formadas por dos o más tipos de polígonos regulares. Un polígono regular es una figura con todos sus lados y ángulos iguales, como un cuadrado o un triángulo equilátero.

Además, todos los sólidos arquimedianos tienen algo llamado "vértices uniformes". Esto significa que si te paras en cualquiera de sus esquinas (vértices), verás el mismo patrón de caras y aristas a tu alrededor.

La mayoría de estos sólidos se pueden obtener a partir de los sólidos platónicos mediante un proceso llamado truncamiento. Imagina que "cortas" las esquinas o los bordes de un sólido platónico para crear nuevas caras.

El famoso matemático griego Arquímedes fue quien describió estos cuerpos hace mucho tiempo. Sus escritos originales se perdieron, pero fueron redescubiertos por artistas y matemáticos durante el Renacimiento, un periodo de gran avance en el arte y la ciencia.

¿Cómo se forman los sólidos arquimedianos?

Muchos sólidos arquimedianos se crean a partir de los sólidos platónicos, que son cinco poliedros muy simétricos (tetraedro, cubo, octaedro, dodecaedro, icosaedro).

Sólidos obtenidos por truncamiento directo

Siete de los sólidos arquimedianos se forman directamente al "cortar" las esquinas de los sólidos platónicos:

• el tetraedro truncado
• el cuboctaedro
• el cubo truncado
• el octaedro truncado
• el icosidodecaedro
• el dodecaedro truncado
• el icosaedro truncado

Sólidos formados por operaciones más complejas

Otros sólidos arquimedianos se obtienen a partir de los ya mencionados, con operaciones un poco más elaboradas:

• Los dos rombicuboctaedros se pueden formar a partir del cuboctaedro. Esto se logra cortando y moviendo las caras de una manera específica.
• De manera similar, los dos rombicosidodecaedros se obtienen del icosidodecaedro con operaciones parecidas.

Sólidos con formas de espejo (enantiomorfas)

Algunos sólidos arquimedianos tienen dos versiones que son como imágenes de espejo una de la otra, pero no se pueden superponer. A estas se les llama formas "enantiomorfas".

• El cubo romo (o cuboctaedro romo) tiene dos formas enantiomorfas. Se obtienen de un rombicuboctaedro menor mediante una transformación que incluye rotar algunas de sus caras y cambiar la forma de otras. La dirección de la rotación decide si obtienes la versión "izquierda" o "derecha".
• Lo mismo ocurre con el dodecaedro romo (o icosidodecaedro romo), que también tiene dos formas enantiomorfas. Se forman de manera similar a partir del rombicosidodecaedro menor.

Características especiales de algunos sólidos arquimedianos

El cuboctaedro y el icosidodecaedro son casos especiales. El cuboctaedro es el resultado de truncar tanto un cubo como un octaedro de una manera específica. El icosidodecaedro es el resultado de truncar un dodecaedro y un icosaedro de forma similar.

Estos dos sólidos son los únicos arquimedianos que tienen todas sus aristas (los bordes donde se unen dos caras) de la misma longitud. Por esta razón, se les considera sólidos semirregulares.

¿Cómo se describen los vértices?

Como en los vértices de los sólidos arquimedianos se juntan diferentes tipos de polígonos, existe una forma de describirlos. Por ejemplo, si en un vértice se encuentran un triángulo y dos pentágonos, se dice que ese vértice tiene una "configuración" 3.5.5. El número 3 representa el triángulo, y los dos 5 representan los dos pentágonos. Este sistema ayuda a entender la estructura de cada vértice.

Sólidos arquimedianos
Número de Sólido	Nombre	Imagen	Caras		Aristas	Vértices	Grupo puntual
1	Tetraedro truncado	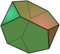Animación	8	4 × {6} 4 × {3}	18	12 × 3.6.6	Td
2	Cuboctaedro	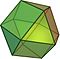Animación	14	6 × {4} 8 × {3}	24	12 × 3.4.3.4	Oh
3	Cubo truncado	Animación	14	6 × {8} 8 × {3}	36	24 × 3.8.8	Oh
4	Octaedro truncado	Animación	14	8 × {6} 6 × {4}	36	24 × 4.6.6	Oh
5	Rombicuboctaedro o rombicuboctaedro menor	Animación	26	18 × {4} 8 × {3}	48	24 × 3.4.4.4	Oh
6	Cuboctaedro truncado o rombicuboctaedro mayor	Animación	26	6 × {8} 8 × {6} 12 × {4}	72	48 × 4.6.8	Oh
7	Cubo romo o cuboctaedro romo (2 formas enantiomorfas)	Animación Animación	38	6 × {4} 32 × {3}	60	24 × 3.3.3.3.4	O
8	Icosidodecaedro	Animación	32	12 × {5} 20 × {3}	60	30 × 3.5.3.5	Ih
9	Dodecaedro truncado	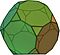Animación	32	12 × {10} 20 × {3}	90	60 × 3.10.10	Ih
10	Icosaedro truncado	Animación	32	20 × {6} 12 × {5}	90	60 × 5.6.6	Ih
11	Rombicosidodecaedro o rombicosidodecaedro menor	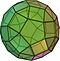Animación	62	12 × {5} 30 × {4} 20 × {3}	120	60 × 3.4.5.4	Ih
12	Icosidodecaedro truncado o rombicosidodecaedro mayor	Animación	62	30 × {4} 20 × {6} 12 × {10}	180	120 × 4.6.10	Ih
13	Dodecaedro romo o icosidodecaedro romo (2 formas enantiomorfas)	Animación Animación	92	12 × {5} 80 × {3}	150	60 × 3.3.3.3.5	Ih

Galería de imágenes

• 

  Tetraedro truncado

• 

  Cuboctaedro

• 

  Cubo truncado

• 

  Octaedro truncado

• 

  Rombicuboctaedro

• 

  Cuboctaedro truncado

• 

  Cubo romo (una forma)

• 

  Icosidodecaedro

• 

  Dodecaedro truncado

• 

  Icosaedro truncado

• 

  Rombicosidodecaedro

• 

  Icosidodecaedro truncado

• 

  Dodecaedro romo (una forma)

Véase también

En inglés: Archimedean solid Facts for Kids

• Arquímedes
• Sólidos de Catalan
• Truncamiento (geometría)