Politopo para niños
En geometría, un politopo es una forma geométrica que generaliza ideas como los polígonos (figuras de dos dimensiones como un cuadrado o un triángulo) y los poliedros (figuras de tres dimensiones como un cubo o una pirámide). Piensa en un politopo como una figura con muchas "caras" o "lados", pero que puede existir en cualquier número de dimensiones, no solo en dos o tres.
El nombre "politopo" viene del alemán polytop, que significa "muchos lugares". Fue creado por Alicia Boole Stott, la hija del famoso matemático y filósofo irlandés George Boole.
Los sólidos platónicos, que son politopos muy especiales de tres dimensiones (como el cubo o el dodecaedro), fueron estudiados por los matemáticos de la Grecia Antigua. Hoy en día, los politopos se usan en muchas áreas, como en los gráficos por computadora para crear imágenes y animaciones, y en la optimización para encontrar las mejores soluciones a problemas.
Contenido
¿Qué son los politopos convexos?
Una clase importante de politopos son los politopos convexos. Imagina que tienes un grupo de puntos. El politopo convexo es la forma más pequeña que puedes crear que encierra todos esos puntos. Es como estirar una goma elástica alrededor de ellos.
También puedes pensar en un politopo convexo como el área donde se cruzan varios "semiespacios". Un semiespacio es como la mitad de un espacio, dividido por una superficie plana. Por ejemplo, en dos dimensiones, una línea divide el plano en dos semiespacios. En tres dimensiones, un plano divide el espacio en dos semiespacios.
Partes de un politopo convexo
Un politopo convexo tiene diferentes partes, que se llaman "caras".
- Una cara de dimensión 0 es un vértice (una esquina).
- Una cara de dimensión 1 es una arista (un borde o línea que conecta dos vértices).
- Las caras de dimensión 2 son las superficies planas que forman el politopo (como los lados de un cubo).
- Las caras de dimensión 3 se llaman celdas.
Estas partes se conectan entre sí. Por ejemplo, dos caras de un politopo se encuentran en una arista.
¿Cómo se construyen los politopos?
Podemos entender los politopos pensando en cómo se construyen a partir de formas más simples.
Construyendo con segmentos de línea
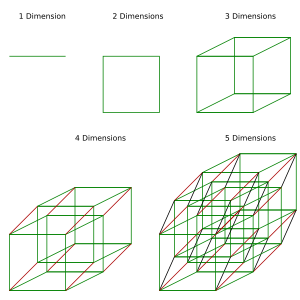
Comencemos con un segmento de línea, que es un politopo de 1 dimensión. Si unimos varios segmentos de línea por sus extremos, podemos formar una curva poligonal.
Si una curva poligonal se cierra (es decir, el punto inicial y final se unen) y no se cruza a sí misma, forma un polígono. Los polígonos son politopos de 2 dimensiones. Por ejemplo, un cuadrado es un polígono.
De polígonos a poliedros y más allá
Podemos seguir este proceso. Si unimos varios polígonos por sus lados, podemos crear superficies tridimensionales. Si estas superficies se cierran, forman un poliedro. Los poliedros son politopos de 3 dimensiones, como un cubo o una pirámide.
De la misma manera, podemos unir poliedros para construir formas de 4 dimensiones, que a veces se llaman "polícoros", y así sucesivamente para dimensiones aún mayores.
Usos de los politopos
Los politopos son muy útiles en el campo de la optimización. Por ejemplo, en la programación lineal, se usan para encontrar los valores máximos o mínimos de una función, pero solo dentro de los límites de un politopo. Esto ayuda a resolver problemas donde se busca la mejor solución posible, como planificar rutas de entrega o asignar recursos.
Véase también
 En inglés: Polytope Facts for Kids
En inglés: Polytope Facts for Kids
- Politopo abstracto
- Politopo regular
- Poliforma
- Polícoro
- Poliedro
- Polígono
- Simplex