Cuboctaedro para niños
Datos para niños Cuboctaedro |
||
|---|---|---|
| Familia: Sólidos de Arquímedes | ||
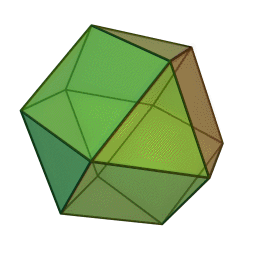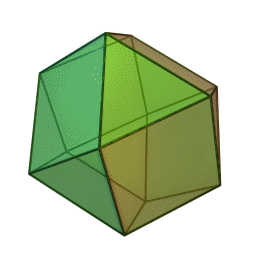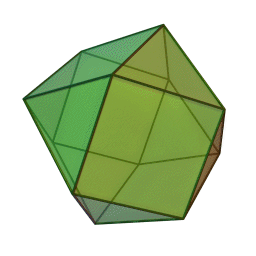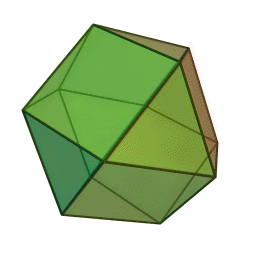 Imagen del sólido
|
||
| Caras | 14 | |
| Aristas | 24 | |
| Vértices | 12 | |
| Configuración de vértices | Uniforme de Orden 4 2 Triángulos 2 Cuadrados En serie:3, 4, 3, 4 |
|
| Grupo de simetría | Octaédrico (Oh) | |
| Poliedro dual | Rombododecaedro | |
| Ángulo diedro | 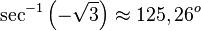 |
|
| Símbolo de Wythoff | 2 | 3 4 | |
| Propiedades | ||
| Poliedro convexo, de vértices uniformes y aristas uniformes | ||
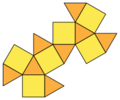
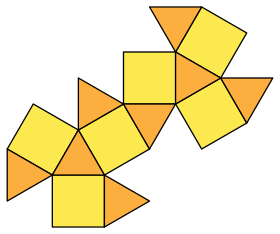
| Desarrollo | ||
 |
||
El cuboctaedro es una forma geométrica tridimensional muy especial. Pertenece a un grupo de figuras llamadas Sólidos de Arquímedes. Imagina una figura con caras planas, bordes rectos y esquinas puntiagudas; el cuboctaedro es una de ellas.
Este sólido tiene 14 caras en total: 6 de ellas son cuadradas y las otras 8 son triángulos equiláteros. Además, cuenta con 24 aristas (los bordes donde se unen las caras) y 12 vértices (las esquinas).
Contenido
Cuboctaedro: Una Forma Geométrica Fascinante
El cuboctaedro es un ejemplo de Sólidos de Arquímedes. Estos son poliedros (formas 3D con caras planas) que tienen caras de diferentes tipos de polígonos regulares. Además, todos sus vértices son iguales, lo que significa que en cada esquina se unen las mismas caras en el mismo orden.
¿Cómo se Forma un Cuboctaedro?
Una de las maneras más interesantes de entender el cuboctaedro es viendo cómo se puede crear a partir de otras formas más simples.
Cortando un Cubo
Imagina un cubo perfecto. Si "cortas" o "truncas" cada una de sus 8 esquinas (vértices) de una manera específica, justo hasta el punto medio de cada arista, ¡obtienes un cuboctaedro! Las 6 caras cuadradas originales del cubo se hacen más pequeñas, y en el lugar de cada esquina cortada, aparece una nueva cara triangular.
Cortando un Octaedro
De forma similar, puedes empezar con un octaedro regular. Un octaedro es una forma con 8 caras triangulares. Si cortas las esquinas de un octaedro de la misma manera, también obtendrás un cuboctaedro. Esto demuestra que el cuboctaedro tiene una relación muy cercana tanto con el cubo como con el octaedro.
Características Especiales del Cuboctaedro
El cuboctaedro tiene propiedades que lo hacen único y simétrico.
Simetría y Equilibrio
Este sólido es muy simétrico. Esto significa que puedes girarlo de muchas maneras y seguirá luciendo igual. Su grupo de simetría es octaédrico, lo que indica que comparte muchas de las simetrías de un octaedro y un cubo.
Caras y Vértices
Como mencionamos, el cuboctaedro tiene 14 caras: 6 cuadrados y 8 triángulos. En cada uno de sus 12 vértices, se unen exactamente dos triángulos y dos cuadrados. Este patrón es siempre el mismo en todas las esquinas, lo que lo convierte en un poliedro de vértices uniformes.
El Poliedro Dual: Rombododecaedro
Cada poliedro tiene un "poliedro dual". Piensa en ello como su forma "opuesta" o "complementaria". Para el cuboctaedro, su poliedro dual es el Rombododecaedro. En un poliedro dual, las caras de uno corresponden a los vértices del otro, y viceversa.
Medidas del Cuboctaedro
Si conoces la longitud de una de las aristas (llamémosla 'a'), puedes calcular el área de su superficie y su volumen.
- El área total de la superficie de un cuboctaedro se calcula con la fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = (6+2\sqrt{3})a^2
- Y su volumen se calcula con:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V = \frac{5}{3} \sqrt{2}a^3
Estas fórmulas nos permiten saber cuánto espacio ocupa y cuánta superficie tiene, dependiendo del tamaño de sus aristas.
Galería de imágenes
Véase también
 En inglés: Archimedean solid Facts for Kids
En inglés: Archimedean solid Facts for Kids
- Sólidos platónicos
- Sólidos de Johnson
- Sólidos de Catalan
- Poliedros duales