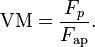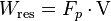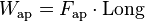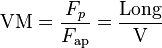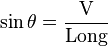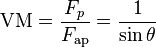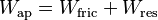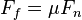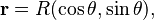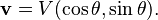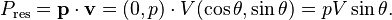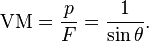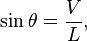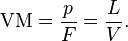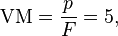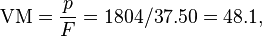Plano inclinado para niños

El plano inclinado (también conocido como rampa o pendiente) es una máquina simple. Imagina una superficie plana que está inclinada, formando un ángulo con el suelo. Se usa para subir objetos a cierta altura. La ventaja principal es que necesitas menos fuerza para mover un objeto por una rampa que si lo levantaras directamente hacia arriba. Eso sí, el objeto recorrerá una distancia mayor y tendrás que vencer la fuerza de rozamiento.

¿Qué es un plano inclinado?

Plano inclinado usado para la educación, Museo Galileo, Florencia

Plano inclinado y las fuerzas que actúan sobre el sólido

Un plano inclinado es una superficie de apoyo que está inclinada, con un extremo más alto que el otro. Se usa para ayudar a subir o bajar cargas. Es una de las seis máquinas simples clásicas que los científicos del Renacimiento identificaron. Se usan mucho para mover cosas pesadas sobre obstáculos altos. Algunos ejemplos son una rampa para cargar cosas en un camión, una persona subiendo una rampa para peatones, o un coche o tren subiendo una cuesta.

Mover un objeto por un plano inclinado requiere menos fuerza que levantarlo directamente. A cambio, el objeto recorre una distancia más larga. La ventaja mecánica de un plano inclinado es la relación entre la longitud de la superficie inclinada y la altura que se sube. Gracias al principio de conservación de la energía, se necesita la misma cantidad de energía mecánica (trabajo) para levantar un objeto a una altura determinada, sin contar las pérdidas por fricción. Sin embargo, el plano inclinado permite hacer el mismo trabajo con menos fuerza, pero aplicándola a lo largo de una distancia mayor.

El ángulo de fricción (a veces llamado ángulo de reposo) es el ángulo máximo en el que un objeto puede quedarse quieto en un plano inclinado sin deslizarse hacia abajo, debido a la fricción. Este ángulo es igual al arcotangente del coeficiente de fricción entre las superficies.

Otras dos máquinas simples se consideran derivadas del plano inclinado. La cuña puede verse como un plano inclinado en movimiento o como dos planos inclinados unidos por la base. El tornillo es como un plano inclinado estrecho que se enrolla alrededor de un cilindro.

El término "plano inclinado" también puede referirse a una aplicación específica, como una rampa recta excavada en una ladera empinada para transportar cosas. Puede incluir vagones sobre raíles o tirados por cables, como un funicular o ferrocarril por cable. Un ejemplo famoso es el Plano Inclinado de Johnstown.

Las reglas que explican cómo se comportan los objetos en un plano inclinado fueron explicadas por primera vez por el matemático Simon Stevin en la segunda mitad del siglo XVI.

¿Qué fuerzas actúan en un plano inclinado?

Para entender las fuerzas que actúan sobre un objeto en un plano inclinado, debemos considerar varias:

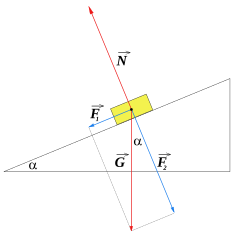
• Primero, la fuerza de gravedad, también conocida como peso. Esta fuerza se debe a la masa (M) del objeto y siempre tira hacia abajo. Su magnitud es M.g y se representa con la letra G.
• Luego, la fuerza normal (N). Esta es la fuerza que el plano ejerce sobre el objeto, empujándolo hacia arriba de forma perpendicular a la superficie del plano. Es una reacción a la fuerza que el objeto ejerce sobre el plano, según la tercera ley de Newton. En la figura, se representa con N.
• Finalmente, la fuerza de rozamiento (F_R). Esta fuerza siempre se opone al movimiento del objeto sobre la superficie. Su magnitud depende del peso del objeto y de las características de las superficies en contacto (lo que se llama coeficiente de rozamiento). Para que el objeto se quede quieto, esta fuerza debe ser igual a la componente del peso que tira hacia abajo por el plano. Si la fuerza que tira hacia abajo es mayor que la fuerza de rozamiento, el objeto se deslizará. Para subir el objeto, se debe aplicar una fuerza que sea igual o mayor que la suma de la fuerza que tira hacia abajo y la fuerza de rozamiento.

Historia de los planos inclinados

Rampa para silla de ruedas, Hotel Montescot, Chartres, Francia

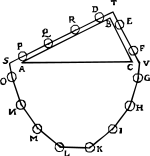
Demostración de Stevin

En 1586, el ingeniero flamenco Simon Stevin (Stevinus) explicó la ventaja mecánica del plano inclinado usando un collar de cuentas. Imaginó dos planos inclinados de la misma altura pero con diferentes pendientes, colocados uno contra el otro como un prisma. Un collar con cuentas a la misma distancia se coloca sobre los planos, con una parte colgando. Las cuentas sobre los planos actúan como cargas. El argumento de Stevin fue: La cadena debe estar quieta, en equilibrio mecánico. Si fuera más pesada de un lado que del otro y empezara a deslizarse, cuando cada cuenta se moviera a la posición de la anterior, la cadena se vería igual que al principio. Esto significaría que seguiría desequilibrada y deslizándose sin parar, lo cual es imposible. Por lo tanto, se queda quieta, y las fuerzas en ambos lados son iguales. La parte de la cadena que cuelga por debajo de los planos es simétrica, con el mismo número de cuentas a cada lado. Ejerce la misma fuerza en cada lado. Por eso, esta parte de la cadena se puede "cortar" sin que afecte el equilibrio de las cuentas que están sobre los planos. Como las cuentas están a la misma distancia en el collar, el número total de cuentas en cada plano es proporcional a la longitud del plano. Como la fuerza de soporte es la misma en ambos lados, la ventaja mecánica de cada plano es proporcional a su longitud inclinada.

Los planos inclinados se han usado desde tiempos muy antiguos para mover objetos pesados. Caminos inclinados y terraplenes construidos por civilizaciones como los romanos son ejemplos de planos inclinados que aún existen y demuestran que entendían su utilidad para mover cargas cuesta arriba. Se cree que las grandes piedras de estructuras antiguas como Stonehenge se movieron usando planos inclinados de tierra, aunque es difícil encontrar pruebas de estas rampas temporales. Las pirámides de Egipto se construyeron con planos inclinados, y las rampas de asedio permitieron a los ejércitos antiguos superar las murallas de las fortalezas. Los antiguos griegos construyeron una rampa pavimentada de 6 km de largo, el Diolkos, para arrastrar barcos por tierra a través del istmo de Corinto.

A pesar de su uso, el plano inclinado fue la última de las seis máquinas simples clásicas en ser reconocida como tal. Esto quizás se deba a que es un dispositivo pasivo y fijo (la carga es lo que se mueve), y también porque se encuentra en la naturaleza como pendientes y colinas. Aunque los filósofos de la antigua Grecia entendían su uso para levantar objetos pesados, no lo incluyeron en su lista de máquinas simples. Esta idea persistió; incluso en 1826, Karl von Langsdorf escribió que un plano inclinado "no es más una máquina que la pendiente de una montaña". El problema de calcular la fuerza necesaria para empujar un peso por un plano inclinado fue analizado por los filósofos griegos Herón de Alejandría y Papo de Alejandría, pero sus soluciones no fueron correctas.

No fue hasta el Renacimiento cuando el plano inclinado se explicó matemáticamente y se clasificó con las otras máquinas simples. El primer análisis correcto apareció en la obra de Jordanus Nemorarius en el siglo XIII, aunque su solución no se difundió mucho. Gerolamo Cardano (1570) propuso una solución incorrecta. Más tarde, a finales del siglo XVI, Michael Varro (1584), Simon Stevin (1586) y Galileo Galilei (1592) publicaron tres soluciones correctas en diez años. Aunque no fue la primera, la explicación de Simon Stevin es la más conocida por su originalidad y el uso del collar de cuentas. En 1600, el científico italiano Galileo incluyó el plano inclinado en su análisis de máquinas simples en Le Meccaniche ("Sobre la mecánica"), mostrando que era un amplificador de fuerza como las otras máquinas.

Las primeras reglas sobre cómo se deslizan los objetos con fricción en un plano inclinado fueron descubiertas por Leonardo da Vinci (1452-1519), pero no se publicaron. Fueron redescubiertas por Guillaume Amontons (1699) y desarrolladas por Charles-Augustin de Coulomb (1785). Leonhard Euler (1750) demostró que la tangente del ángulo de rozamiento interno en un plano inclinado es proporcional a la fricción.

Usos de los planos inclinados

Los planos inclinados se usan mucho como "rampas" para cargar y descargar cosas en camiones, barcos y aviones. Las rampas para sillas de ruedas ayudan a las personas con movilidad reducida a superar obstáculos altos sin mucho esfuerzo. Las escaleras mecánicas y las cintas transportadoras inclinadas también son tipos de planos inclinados. En un funicular o ferrocarril por cable, un vagón de tren sube por un plano inclinado con cables. Los planos inclinados también permiten que personas y objetos pesados o frágiles bajen de forma segura, usando la fuerza normal del plano para distribuir el efecto de la gravedad. Las rampas de evacuación de los aviones permiten que las personas lleguen al suelo de forma rápida y segura desde la altura de la cabina de un avión comercial.

Uso de rampas para cargar un automóvil en un camión

Cargando un camión en un barco usando una rampa

Rampa de evacuación de emergencia de una aeronave

Rampa para silla de ruedas de un autobús japonés

Rampa de carga en un camión

Otros planos inclinados son parte de estructuras permanentes. Las carreteras y vías de tren tienen planos inclinados en forma de pendientes suaves, rampas y terraplenes para que los vehículos puedan superar obstáculos como colinas sin perder agarre. De manera similar, los senderos y las aceras tienen rampas suaves para que los peatones puedan caminar con seguridad. Los planos inclinados también se usan para divertirse, como en toboganes, rampas acuáticas, esquí alpino y pistas de patinaje.

Rampa de tierra (derecha) construida por los romanos en el 72 d. C. para invadir Masada, Israel

Rampa peatonal, Palacio do Planalto, Brasilia

Plano Inclinado de Johnstown, un ferrocarril funicular

Carretera de Burma, Assam, India, desde Burma hacia China (1945)

Planos inclinados en una pista de "skate"

Conceptos importantes del plano inclinado

¿Qué es la pendiente de un plano inclinado?

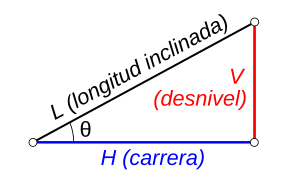
El funcionamiento de un plano inclinado depende de su pendiente, es decir, de su inclinación. Cuanto menos inclinada sea la pendiente, mayor será la ventaja mecánica y menos fuerza necesitarás para levantar un peso. La pendiente s de un plano se calcula dividiendo la diferencia de altura entre sus dos extremos (el "desnivel") por su longitud horizontal (la "carrera"). También se puede expresar por el ángulo θ que forma el plano con la horizontal.

La geometría del plano inclinado se basa en un triángulo rectángulo. La longitud horizontal (H) a veces se llama carrera, y el desplazamiento en altura medido en vertical (V) se llama desnivel

¿Qué es la ventaja mecánica?

La ventaja mecánica VM de una máquina simple es la relación entre la fuerza que se obtiene sobre la carga y la fuerza que se aplica. Para el plano inclinado, la fuerza que hay que vencer es el peso del objeto. La fuerza aplicada es la que se ejerce sobre el objeto, paralela al plano, para moverlo hacia arriba. La ventaja mecánica es:

La ventaja mecánica de un plano inclinado ideal (sin fricción) se llama "ventaja mecánica ideal" (VMI). Cuando se incluye la fricción, se llama "ventaja mecánica real" (VMR).

Plano inclinado sin fricción

Plano inclinado instrumentado utilizado para la enseñanza de la física, alrededor de 1900. El peso de la izquierda proporciona la fuerza a vencer F_p. El peso de la derecha proporciona la fuerza aplicada F_ap tirando del rodillo hacia arriba del plano

Si no hay fricción entre el objeto y el plano, se le llama "plano inclinado ideal". Esto puede ocurrir si el objeto rueda, como un barril, o si tiene ruedas. Por el principio de conservación de la energía, en un plano inclinado sin fricción, el trabajo que se hace para levantar la carga (W_res) es igual a la fuerza aplicada multiplicada por la distancia recorrida (W_ap).

El trabajo se define como la fuerza multiplicada por la distancia que mueve un objeto. El trabajo hecho sobre la carga es igual a su peso multiplicado por la altura que sube.

El trabajo aplicado es igual a la fuerza F_ap ejercida sobre el objeto multiplicada por la longitud diagonal del plano inclinado.

Si sustituimos estos valores en la ecuación de conservación de energía y los reordenamos, obtenemos:

Para expresar la ventaja mecánica usando el ángulo θ del plano, podemos ver en el diagrama que:

Entonces:

Esto significa que la ventaja mecánica de un plano inclinado sin fricción es igual al inverso del seno del ángulo de inclinación. La fuerza aplicada F_ap de esta ecuación es la fuerza necesaria para mantener la carga quieta en el plano inclinado o para empujarla hacia arriba a una velocidad constante. Si la fuerza aplicada es mayor, la carga acelerará hacia arriba; si es menor, acelerará hacia abajo.

Plano inclinado con rozamiento

Cuando hay fricción entre el plano y la carga, como una caja pesada que se desliza por una rampa, parte del trabajo que se aplica se pierde como calor debido a la fricción (W_fric). Por lo tanto, se realiza menos trabajo sobre la carga. Debido a la conservación de la energía, la suma del trabajo útil y las pérdidas por fricción es igual al trabajo aplicado:

Por eso, se necesita más fuerza aplicada y la ventaja mecánica es menor que si no hubiera fricción. Con fricción, la carga solo se moverá si la fuerza neta paralela a la superficie es mayor que la fuerza de fricción F_f que se opone al movimiento. La fuerza de fricción máxima se calcula como:

donde F_n es la fuerza normal entre la carga y el plano (perpendicular a la superficie), y μ es el coeficiente de fricción entre las dos superficies, que cambia según el material. Si no se aplica ninguna fuerza, y el ángulo de inclinación θ del plano es menor que un valor máximo φ, la parte de la fuerza de gravedad paralela al plano será demasiado pequeña para vencer la fricción, y la carga se quedará quieta. Este ángulo se llama ángulo de rozamiento interno y depende de los materiales de las superficies, pero no del peso de la carga. La tangente del ángulo de reposo φ es igual a μ:

Con fricción, siempre hay un rango de fuerza aplicada F_ap para el cual la carga está quieta (no se desliza ni hacia arriba ni hacia abajo). En cambio, en un plano inclinado sin fricción, solo hay un valor específico de fuerza para que la carga esté quieta.

Análisis de fuerzas

Clave: F_n = N = Fuerza normal que es perpendicular al plano, F_ap = f = fuerza aplicada, F_p = mg = peso del objeto, donde m = masa, g = gravedad

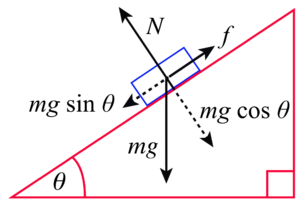
Un objeto que está en un plano inclinado tiene tres fuerzas actuando sobre él:

• La fuerza aplicada, F_ap, que se ejerce sobre el objeto para moverlo, paralela al plano inclinado.
• El peso de la carga, F_p, que siempre tira verticalmente hacia abajo.
• La fuerza del plano sobre la carga, que tiene dos partes:
  • La fuerza normal F_n del plano inclinado sobre la carga, que la soporta. Esta fuerza es perpendicular a la superficie.
  • La fuerza de fricción, F_f del plano sobre la carga, que actúa paralela a la superficie y siempre se opone al movimiento. Es igual a la fuerza normal multiplicada por el coeficiente de fricción μ entre las dos superficies.

Según las leyes de Newton, el objeto estará quieto o en movimiento constante si la suma de las fuerzas sobre él es cero. Como la dirección de la fuerza de fricción es opuesta si el movimiento es hacia arriba o hacia abajo, debemos considerar estos dos casos por separado:

• Movimiento hacia arriba: La fuerza total sobre el objeto es hacia arriba, por lo que la fuerza de fricción se dirige hacia abajo en el plano, oponiéndose a la fuerza aplicada.

La ventaja mecánica es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathrm{VM} = \frac {F_p}{F_{\rm ap}} = \frac {\cos \phi} { \sin (\theta + \phi ) } \,

donde 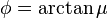. Esta es la condición para que el objeto empiece a moverse hacia arriba del plano inclinado. Si la fuerza aplicada F_ap es mayor que la que indica esta ecuación, el objeto se moverá hacia arriba.

• Movimiento hacia abajo: La fuerza total sobre el objeto es hacia abajo, por lo que la fuerza de fricción se dirige hacia arriba del plano.

La ventaja mecánica es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathrm{VM} = \frac {F_p}{F_{\rm ap}} = \frac {\cos \phi} { \sin (\theta - \phi ) } \,

Esta es la condición para que el objeto empiece a moverse hacia abajo del plano. Si la fuerza aplicada F_i es menor que la que indica esta ecuación, el objeto se deslizará por el plano. Hay tres situaciones:

1. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \theta < \phi\, : La ventaja mecánica es negativa. Si no se aplica fuerza, el objeto se quedará quieto y necesitará una fuerza aplicada hacia abajo para deslizarse.
2. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \theta = \phi\, : Es el ángulo de reposo. La ventaja mecánica es infinita. Sin fuerza aplicada, el objeto no se deslizará, pero la más mínima fuerza hacia abajo hará que se deslice.
3. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \theta > \phi\, : La ventaja mecánica es positiva. Si no se aplica fuerza, el objeto se deslizará por el plano y necesitará una fuerza hacia arriba para mantenerse quieto.

Ventaja mecánica usando la potencia

Clave: N = Fuerza normal que es perpendicular al plano, p=mg, donde m=masa, g=gravedad, y θ(theta)=Ángulo de inclinación del plano

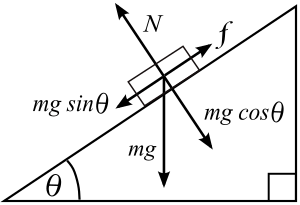
La ventaja mecánica de un plano inclinado es la relación entre el peso de la carga en la rampa y la fuerza necesaria para subirla. Si no se pierde ni se almacena energía en el movimiento, esta ventaja mecánica se puede calcular a partir de las medidas de la rampa.

Para entender esto, imaginemos un vagón en una rampa con un ángulo θ sobre la horizontal. Su posición es:

donde R es la distancia en la rampa. La velocidad del vagón en la rampa es:

Como no hay pérdidas, la potencia que usa la fuerza "F" para subir la carga por la rampa es igual a la potencia que se obtiene, que es la elevación vertical del peso "p" de la carga.

La potencia aplicada para subir el vagón por la rampa es:

y la potencia obtenida es:

Igualando la potencia aplicada y la potencia obtenida, obtenemos la ventaja mecánica:

La ventaja mecánica de una rampa inclinada también se puede calcular a partir de la relación entre la longitud de la rampa L y su altura vertical V, porque el seno del ángulo de la rampa es:

por lo tanto:

Disposición del sistema de accionamiento por cable del plano inclinado de Liverpool Minard

Ejemplo: si la altura de una rampa es V = 1 metro y su longitud es L = 5 metros, entonces la ventaja mecánica es:

Esto significa que una fuerza de 20 kg levantará una carga de 100 kg.

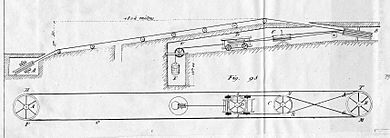
El plano inclinado Liverpool Minard tiene unas medidas de 1804 metros de largo y 37,50 metros de desnivel, lo que da una ventaja mecánica de:

Así, una fuerza de tensión de 100 kp en el cable levantará una carga de 4810 kp. La inclinación de esta pendiente es del 2 %, lo que significa que el ángulo θ es tan pequeño que sen θ es casi igual a tan θ.

Galería de imágenes

• 

  Uso de rampas para cargar un automóvil en un camión

• 

  Cargando un camión en un barco usando una rampa

• 

  Rampa de evacuación de emergencia de una aeronave

• 

  Rampa para silla de ruedas de un autobús japonés

• 

  Rampa de carga en un camión

• 

  Rampa de tierra (derecha) construida por los romanos en el 72 d. C. para invadir Masada, Israel

• 

  Rampa peatonal, Palacio do Planalto, Brasilia

• 

  Plano Inclinado de Johnstown, un ferrocarril funicular

• 

  Carretera de Burma, Assam, India, desde Burma hacia China (1945)

• 

  Planos inclinados en una pista de "skate"

Véase también

En inglés: Inclined plane Facts for Kids