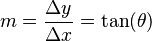Pendiente (matemática) para Niños

La pendiente es una medida que nos dice qué tan inclinada está una línea o una superficie. Imagina una rampa o una carretera: la pendiente nos indica si sube mucho, baja mucho o es casi plana. En matemáticas, especialmente en la geometría analítica, la pendiente nos ayuda a entender cómo se comportan las líneas rectas. Es un concepto muy útil para diseñar carreteras, vías de tren o canales, ya que nos permite saber si son muy empinadas o suaves.

¿Qué es la Pendiente en Matemáticas?

En matemáticas, la pendiente de una línea recta nos dice cuánto cambia la altura (eje Y) por cada paso que damos hacia un lado (eje X). Es como una "tasa de cambio" que nos indica si la línea sube, baja o se mantiene horizontal.

El Ángulo de Inclinación

El ángulo de inclinación es el ángulo que forma una línea recta con el eje horizontal (el eje X). Este ángulo nos da una idea visual de la inclinación. La relación entre este ángulo (llamémoslo α) y la pendiente se da a través de una función matemática llamada tangente.

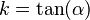
$k = \tan(\alpha)$

Aquí, la letra k representa la pendiente, y tan es la función tangente. Así, la pendiente y el "coeficiente angular" son lo mismo: ambos describen la inclinación de la línea.

Calculando la Pendiente de una Recta

Pendiente:

m=\frac{\Delta y}{\Delta x}=\tan( \theta )

La pendiente de una recta se suele representar con la letra m. Nos dice si la línea está subiendo (pendiente positiva), bajando (pendiente negativa), es completamente plana (pendiente cero) o es vertical (pendiente indefinida).

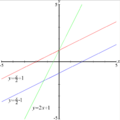
Si la pendiente es positiva, la línea sube de izquierda a derecha.
Si la pendiente es negativa, la línea baja de izquierda a derecha.
Si la pendiente es cero (0), la línea es horizontal, como el eje X. Por ejemplo, una línea donde y siempre es 2 (y=2) tiene pendiente cero.
Si la pendiente es indefinida (o "infinita"), la línea es vertical, como el eje Y. Por ejemplo, una línea donde x siempre es 3 (x=3) tiene pendiente indefinida.

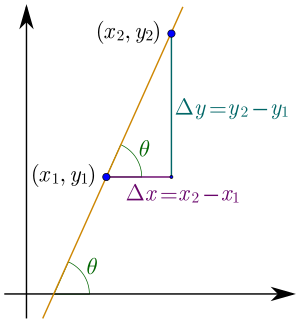
Para calcular la pendiente de una recta, necesitamos dos puntos distintos de esa recta. Si tenemos los puntos (x1, y1) y (x2, y2), la fórmula es:

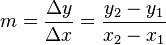
$m = \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1}$

Aquí, Δy (delta y) significa la diferencia en las coordenadas Y, y Δx (delta x) significa la diferencia en las coordenadas X.

La Pendiente y la Geometría de las Líneas

Una línea horizontal tiene una pendiente de 0. Cuanto más grande sea el valor de la pendiente (ya sea positivo o negativo), más inclinada estará la línea. Por ejemplo, una línea que sube con un ángulo de 45° tiene una pendiente de +1. Una línea que baja con un ángulo de 30° tiene una pendiente de aproximadamente -0.5.

El ángulo (θ) que una línea forma con el eje horizontal se relaciona con la pendiente (m) de esta manera:

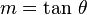
$m = \tan\,\theta$

O, para encontrar el ángulo si ya conoces la pendiente:

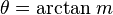
$\theta = \arctan\,m$

Líneas Paralelas y Perpendiculares

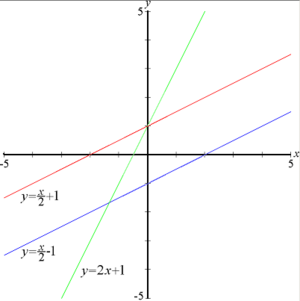
Líneas paralelas: Dos o más líneas son paralelas si tienen la misma pendiente. Esto significa que nunca se cruzarán.
Líneas perpendiculares: Dos o más líneas son perpendiculares si forman un ángulo recto (90°) entre sí. Esto ocurre si al multiplicar sus pendientes, el resultado es -1.

La Pendiente en las Ecuaciones de la Recta

Tres líneas rectas — Las líneas roja y azul tienen la misma pendiente (m) que es ½, mientras que las líneas roja y verde se cruzan con el eje Y en el mismo punto, que es el punto x=0, y=1.

La pendiente es un elemento clave en las ecuaciones que describen una línea recta.

Forma pendiente-ordenada al origen:

$y = mx + b \,$

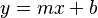
En esta ecuación, m es la pendiente. El valor de b es el punto donde la línea cruza el eje Y (cuando x es 0). A este punto se le llama "ordenada al origen".

Forma pendiente-abscisa al origen:

$y=m(x - a) \,$

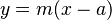
Aquí, m sigue siendo la pendiente. El valor de a es el punto donde la línea cruza el eje X (cuando y es 0). A este punto se le llama "abscisa al origen".

Ecuación de la recta con un punto y la pendiente:

Si conoces la pendiente m y un punto (x0, y0) por el que pasa la recta, puedes encontrar su ecuación usando:

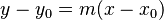
$y - y_0 = m(x - x_0) \,$

Pendiente desde la forma general de la ecuación:

Si la ecuación de la recta está en la forma general:

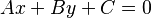
$Ax + By + C = 0 \,$

La pendiente se calcula como:

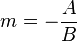
$m = -\frac{A}{B}$

Propiedades Importantes de la Pendiente

Si tienes las pendientes de dos líneas (k1 y k2), puedes calcular el ángulo entre ellas usando una fórmula que involucra la tangente.
Para que dos líneas sean paralelas, sus pendientes deben ser iguales (k1 = k2).
Para que dos líneas sean perpendiculares, el producto de sus pendientes debe ser -1 (k1 * k2 = -1).

La Pendiente en el Cálculo

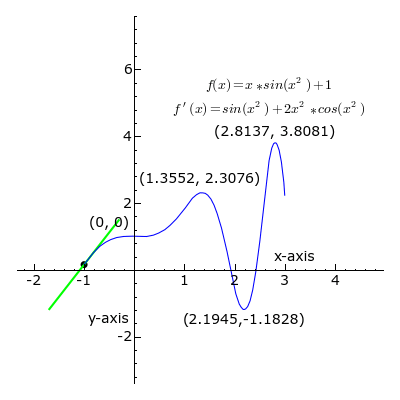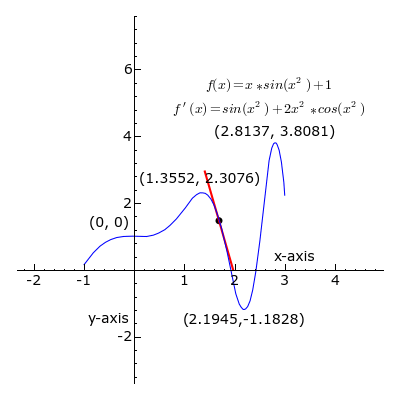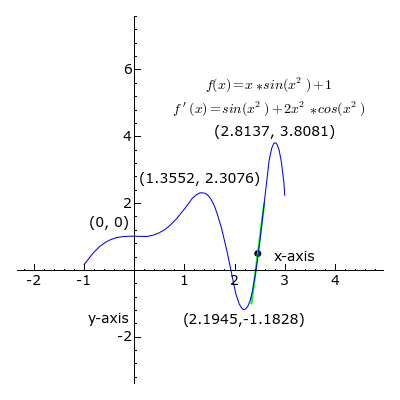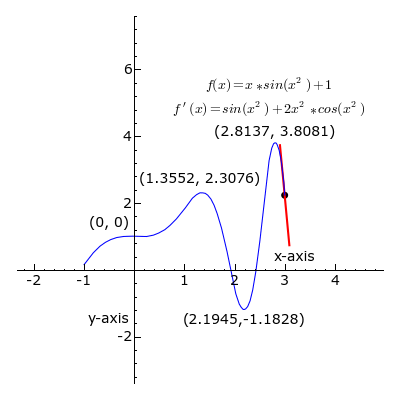
Archivo:Graph of sliding derivative line

Representación gráfica de la derivada.

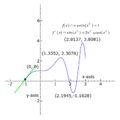
El concepto de pendiente es muy importante en una rama de las matemáticas llamada cálculo diferencial. En el cálculo, la pendiente no solo se aplica a líneas rectas, sino también a curvas. Para una curva, la pendiente cambia en cada punto. La derivada de una función en un punto específico nos da la pendiente de la línea que "toca" la curva en ese punto (llamada línea tangente). Esto nos ayuda a entender cómo una cantidad cambia en un momento dado.

Galería de imágenes

Pendiente: $m=\frac{\Delta y}{\Delta x}=\tan( \theta )$
Tres líneas rectas — Las líneas roja y azul tienen la misma pendiente (m) que es ½, mientras que las líneas roja y verde se cruzan con el eje Y en el mismo punto, que es el punto x=0, y=1.
Representación gráfica de la derivada.

Véase también

En inglés: Slope Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Pendiente_(matemática)&oldid=4966980»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Pendiente (matemática) para Niños. Enciclopedia Kiddle.

Pendiente (matemática) para niños