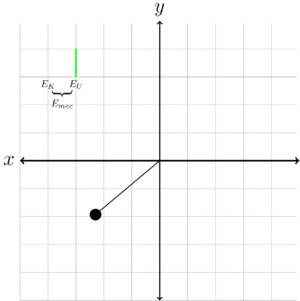
Energía mecánica para niños

La energía mecánica de un objeto o de un sistema es la suma de su energía cinética (la energía del movimiento) y su energía potencial (la energía de la posición). Es una cantidad que nos ayuda a entender cómo se mueven los cuerpos y cómo actúan las fuerzas mecánicas, como la gravedad o las fuerzas de los resortes (como la ley de Hooke). Estas fuerzas son especiales porque "guardan" la energía.

La energía cinética está relacionada con la masa de un objeto y su velocidad. Cuanto más pesado y rápido sea algo, más energía cinética tendrá. La energía potencial, en cambio, depende de la posición del objeto y de las fuerzas que actúan sobre él. Por ejemplo, una pelota en lo alto de una colina tiene energía potencial debido a la gravedad.

Un principio muy importante en física es la conservación de la energía. Dice que, si no hay otras fuerzas actuando, la suma de la energía potencial y la energía cinética de un objeto siempre se mantiene igual. Esa suma es la energía mecánica.

Sin embargo, en el mundo real, siempre hay fuerzas que no "guardan" la energía, como la fricción (el rozamiento). Estas fuerzas hacen que la energía mecánica no se conserve perfectamente, sino que se transforme en otras formas de energía, como el calor. Pero si la fricción es muy pequeña, podemos decir que la energía mecánica se conserva casi por completo. Para entender bien la energía mecánica, es clave saber qué tipo de fuerzas están actuando.

¿Qué es la Energía Mecánica?

Los seres humanos hemos usado la energía mecánica desde hace mucho tiempo. Por ejemplo, los griegos inventaron las poleas y los engranajes. Los romanos usaban catapultas para lanzar proyectiles. En una catapulta, al comprimir el brazo, se almacena energía potencial. Luego, esta energía se libera y se convierte en energía cinética, que es la energía de movimiento del proyectil. Parte de esa energía también se convierte en calor debido a la fricción en las cuerdas y engranajes.

Un péndulo simple demuestra cómo la energía mecánica se transforma entre energía potencial gravitacional y energía cinética.

La energía es una cantidad que nos ayuda a describir el movimiento. Es más fácil de usar que las fuerzas directamente. La energía aparece en muchas áreas de la física, como la mecánica, el electromagnetismo y las ondas. El concepto de energía está muy relacionado con el trabajo y el calor, que son formas en que la energía se transfiere.

La energía siempre se conserva en cualquier proceso físico. Esto significa que la cantidad total de energía antes de un proceso es la misma que después, aunque pueda cambiar de una forma a otra.

La energía mecánica tiene dos partes principales: la energía cinética, que es la energía del movimiento y depende de la masa y la velocidad de un cuerpo; y la energía potencial, que está relacionada con las fuerzas de la gravedad o las fuerzas elásticas. La energía potencial depende de la masa del cuerpo y de su posición. Un ejemplo sencillo de energía potencial es la que tiene un objeto debido a su peso cuando está a cierta altura sobre la Tierra.

La suma de la energía cinética y la energía potencial de un objeto en un momento y lugar específicos es lo que llamamos energía mecánica. En este artículo, veremos estas ideas y cómo se expresa la energía según las fuerzas que actúan o las aplicaciones, ya sea en líquidos, gases o sólidos. También es importante considerar la fricción, que hace que se pierda energía mecánica en forma de calor.

Además de la energía, el trabajo y el calor, otra cantidad importante es la potencia mecánica. La potencia nos dice qué tan rápido se usa o produce energía. Para entender la energía mecánica, necesitamos saber cómo se calculan la energía cinética en movimientos de traslación (en línea recta) y rotación (girando), y la energía potencial gravitatoria o elástica.

Energía Cinética: La Energía del Movimiento

La energía cinética es la energía que tienen los objetos debido a su movimiento.

¿Cómo se calcula la Energía Cinética?

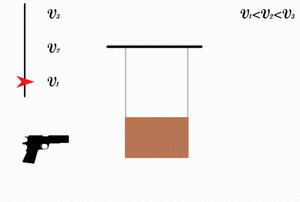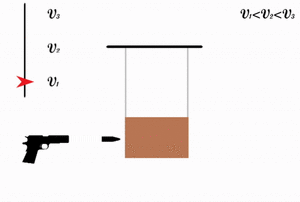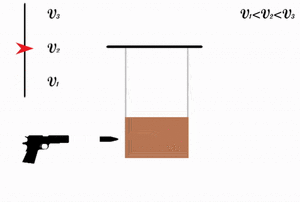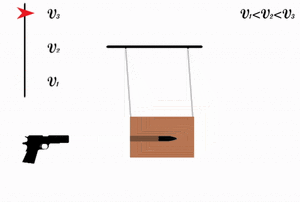
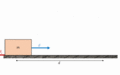
Imagina un bloque de masa m que se mueve en una superficie horizontal con una velocidad v. La energía cinética de este bloque es igual al trabajo que una fuerza tuvo que hacer para que el bloque pasara de estar quieto (velocidad cero) a tener esa velocidad v. El bloque ha ganado energía mecánica, que ahora es energía cinética, gracias a ese trabajo.

La fórmula para la energía cinética es: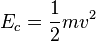

Esto significa que la energía cinética depende de la masa (m) y de la velocidad (v) al cuadrado. Cuanto mayor sea la masa o la velocidad, mayor será la energía cinética.

También podemos pensar en la energía cinética como el trabajo que una fuerza debe hacer para detener un objeto en movimiento. La energía cinética es una cantidad que no tiene dirección ni sentido, y siempre es mayor o igual a cero. Cuando un objeto se detiene, pierde toda su energía mecánica inicial.

Péndulo balístico: La energía cinética de la bala se transfiere al bloque, haciéndolo subir. En el punto más alto, toda la energía cinética inicial se convierte en energía potencial.

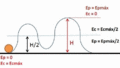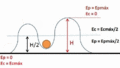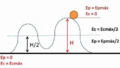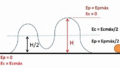
Un buen ejemplo para entender la energía cinética es un péndulo. Si sueltas la masa de un péndulo desde un lado, al bajar, pierde altura y su energía potencial disminuye. Pero no se detiene en el punto más bajo; sigue moviéndose gracias a la energía cinética. Al subir al otro lado, la energía cinética disminuye y se convierte de nuevo en energía potencial. Este proceso se repite.

La energía cinética que el péndulo tiene en su punto más bajo es igual a la energía potencial máxima que tenía en su punto más alto. Esto se debe a que la energía mecánica del péndulo se conserva (si no hay fricción).

Energía Cinética en Movimientos de Rotación

Cuando un objeto gira alrededor de un eje, también tiene energía cinética. En este caso, en lugar de la masa, usamos el "momento de inercia" (que nos dice qué tan difícil es hacer girar un objeto) y en lugar de la velocidad lineal, usamos la "velocidad angular" (qué tan rápido gira).

La fórmula para la energía cinética de rotación es: 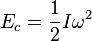Donde I es el momento de inercia y ω es la velocidad angular.

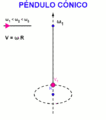
Un ejemplo es el péndulo cónico. Cuanto más rápido gira, más energía cinética de rotación tiene y más alto sube.

Energía Potencial: La Energía de la Posición

La energía potencial es la energía que un objeto tiene debido a su posición o estado.

Energía Potencial Gravitatoria: La Fuerza de la Tierra

La fuerza gravitatoria es la fuerza de atracción que la Tierra ejerce sobre los objetos. La energía potencial gravitatoria depende de la masa del objeto y de su distancia al centro de la Tierra.

La fórmula general para la energía potencial gravitatoria es: 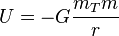Donde G es la constante de gravitación universal, m_T es la masa de la Tierra, m es la masa del objeto y r es la distancia entre el centro de la Tierra y el objeto.

Un satélite orbitando la Tierra. Como la gravedad es una fuerza conservativa, la energía mecánica se mantiene constante.

Cuando un objeto está cerca de la superficie de la Tierra, la fórmula de la energía potencial gravitatoria se simplifica mucho. En lugar de tomar el infinito como punto de referencia, tomamos el suelo como el punto donde la energía potencial es cero.

La expresión más común para la energía potencial gravitatoria cerca de la superficie terrestre es: 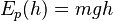Donde m es la masa del objeto, g es la aceleración de la gravedad (aproximadamente 9.8 m/s² en la Tierra) y h es la altura del objeto sobre el suelo.

Esto significa que cuanto más alto esté un objeto, más energía potencial gravitatoria tendrá. Si un objeto cae, su energía potencial se convierte en energía cinética.

Energía Potencial Elástica: La Energía de los Resortes

El sistema oscilatorio más simple: una masa sujeta a un muelle.

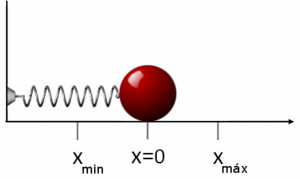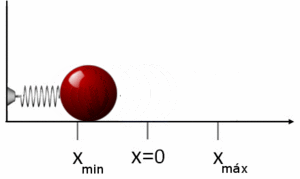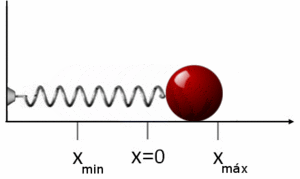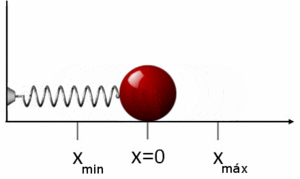
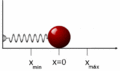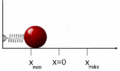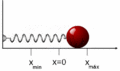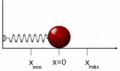
Un resorte es un buen ejemplo para entender la energía potencial elástica. Cuando estiras o comprimes un resorte, este almacena energía. La fuerza que hace el resorte para volver a su posición original se llama fuerza elástica, y sigue la ley de Hooke: 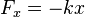, donde k es la constante elástica del resorte y x es cuánto se estiró o comprimió.

La energía potencial elástica almacenada en un resorte estirado o comprimido es: 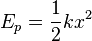Esta energía es máxima cuando el resorte está muy estirado o muy comprimido, y es cero cuando el resorte está en su longitud natural (equilibrio).

Si un objeto está sujeto a un resorte y también afectado por la gravedad, su energía potencial total será la suma de la energía potencial gravitatoria y la energía potencial elástica.

La Conservación de la Energía Mecánica

El principio de conservación de la energía es una ley fundamental en física. Dice que la energía total de un sistema aislado (que no intercambia energía con su entorno) siempre se mantiene constante, aunque pueda transformarse de una forma a otra (por ejemplo, de energía eléctrica a energía mecánica).

Sin embargo, la energía mecánica por sí misma no siempre se conserva. Esto ocurre cuando hay fuerzas que no son "conservativas", como la fricción.

¿Qué pasa con la Fricción?

Cuando hay fricción (rozamiento), parte de la energía mecánica se transforma en otras formas de energía, principalmente calor. Por ejemplo, si un bloque se desliza por una rampa con rozamiento, la energía mecánica inicial del bloque no será igual a la final, porque parte de esa energía se habrá convertido en calor debido al rozamiento.

La disminución de la energía mecánica es igual al trabajo realizado por las fuerzas de fricción. Las fuerzas de fricción siempre se oponen al movimiento, por lo que el trabajo que realizan es negativo, lo que significa que "quitan" energía mecánica del sistema.

Si consideramos la energía total de un sistema, incluyendo la energía que se disipa como calor debido a la fricción, entonces la energía total sí se conserva. Es decir, la energía mecánica inicial es igual a la energía mecánica final más la energía disipada por la fricción.

Trabajo y Potencia: Conceptos Clave

Para entender la energía mecánica, es importante conocer el trabajo y la potencia.

¿Qué es el Trabajo en Física?

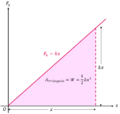
El trabajo es una forma de transferir energía. Se realiza cuando una fuerza mueve un objeto a lo largo de una distancia. El trabajo se mide en julios (J), igual que la energía.

Si una fuerza constante F mueve un objeto una distancia s en la misma dirección, el trabajo realizado es:

Cuando las fuerzas conservativas (como la gravedad o la fuerza de un muelle) realizan trabajo sobre un objeto, cambian su energía cinética. Si el trabajo es positivo, la energía cinética aumenta; si es negativo, disminuye.

¿Qué es la Potencia?

La potencia es la rapidez con la que se realiza el trabajo. Nos dice cuánto trabajo se hace en un determinado tiempo. Se mide en vatios (W) en el Sistema Internacional.

La potencia media se calcula como: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P_{med} = \frac{\Delta W}{\Delta t} Donde ΔW es el trabajo realizado y Δt es el tiempo que tardó en hacerse.

La potencia instantánea (en un momento específico) se calcula como: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P = \vec{F} \cdot \vec{v} Donde F es la fuerza y v es la velocidad del objeto.

Aplicaciones de la Energía Mecánica

La energía mecánica se aplica en muchos campos de la física y la ingeniería.

Energía en Fluidos: El Principio de Bernoulli

El principio de Bernoulli es una forma de la conservación de la energía aplicada a los fluidos (líquidos y gases) en movimiento. Nos ayuda a entender cómo la velocidad, la presión y la altura de un fluido se relacionan. Por ejemplo, explica por qué los aviones pueden volar (sustentación aerodinámica) o cómo funciona el efecto Venturi.

La ecuación de Bernoulli, en su forma más sencilla, dice que la suma de la presión, la energía potencial por unidad de volumen y la energía cinética por unidad de volumen es constante a lo largo de una línea de corriente en un fluido ideal (sin fricción).

Energía en Máquinas Térmicas: El Primer Principio de la Termodinámica

El primer principio de la termodinámica es otra forma de la conservación de la energía, pero aplicada a sistemas que intercambian calor y trabajo con su entorno, como las máquinas térmicas. Estas máquinas, como las de una central térmica o nuclear, usan calor para producir trabajo mecánico.

El principio se expresa como: 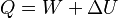Donde Q es el calor suministrado, W es el trabajo realizado y ΔU es el cambio en la energía interna del sistema (la energía de las moléculas que lo componen).

Esto significa que el calor que entra en una máquina se usa para hacer trabajo y para cambiar la energía interna de la máquina.

Energía en Movimientos Vibratorios: Oscilaciones

Un sistema masa-resorte en movimiento armónico simple.

El movimiento armónico simple (M.A.S.) es el tipo de oscilación más sencillo, como el de una masa unida a un resorte que se mueve horizontalmente sin fricción. En este caso, la energía mecánica se conserva. La energía se transforma continuamente entre energía cinética (cuando la masa se mueve más rápido) y energía potencial elástica (cuando el resorte está más estirado o comprimido).

La energía mecánica total en un M.A.S. es constante: 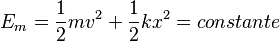Donde m es la masa, v la velocidad, k la constante del resorte y x el desplazamiento.

Cuando hay fuerzas de fricción (como la resistencia del aire), las oscilaciones se van "amortiguando" y la energía mecánica disminuye con el tiempo, transformándose en calor. Por eso, un péndulo o una campana no oscilan para siempre.

Tipos de Energía Mecánica en la Naturaleza

Algunos ejemplos de cómo se aprovecha la energía mecánica en la naturaleza son:

• Energía hidráulica: Se usa la energía potencial del agua que cae para generar energía eléctrica o mover molinos.
• Energía eólica: Es la energía del viento. Se usa para generar electricidad con aerogeneradores o para bombear agua. Es un tipo de energía cinética.
• Energía mareomotriz: Es la energía del movimiento de las mareas y las olas del mar. También es un tipo de energía cinética.

Galería de imágenes

• 

  Un péndulo simple demostrando la conservación de la energía mecánica entre la energía potencial gravitacional y la energía cinética

• 

  Justificación gráfica de la conservación de la energía mecánica. En el punto más bajo, la energía mecánica de la bola es solo energía cinética, sin embargo, en el punto más alto, toda la energía mecánica pasa a ser energía potencial.

• 

  Trabajo de una fuerza.

• 

  El péndulo cónico puede actuar como un selector de velocidades, a mayor par de fuerzas ejercido sobre el péndulo, mayor velocidad alcanzará, mayor será su energía cinética de rotación y, por tanto, mayor será la altura alcanzada.

• 

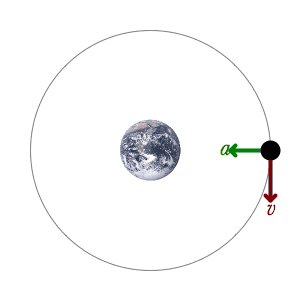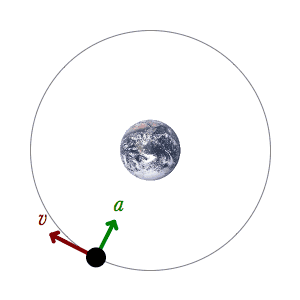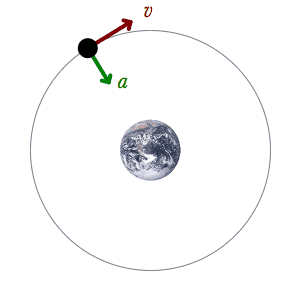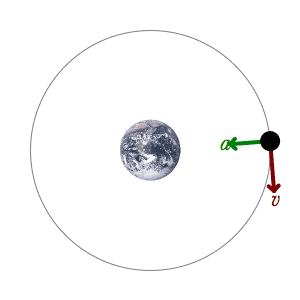
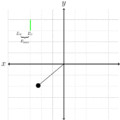
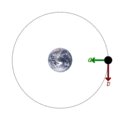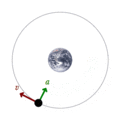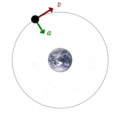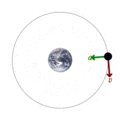
  En este ejemplo, un satélite está orbitando alrededor de la Tierra atraído únicamente por una fuerza gravitatoria, que es una fuerza conservativa, por lo tanto la energía mecánica se conserva. Al ser un movimiento circular, la energía potencial depende de la altura del satélite y es constante, por lo tanto la energía cinética es también constante. En consecuencia, el módulo de la velocidad del satélite es constante. En la imagen se representa la aceleración con un vector verde, y la velocidad con un vector rojo . Si la órbita que sigue el satélite fuera una elipse, la energía potencial y la energía cinética variarían con el tiempo pero su suma permanecería constante.

• 

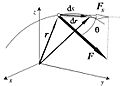
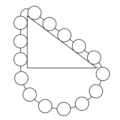
  Epitafio de Stevin: El número de bolas de la cadena, que 'cuelgan' en la vertical del plano inclinado, proporciona una idea intuitiva de la energía potencial de la parte de la cadena que yace sobre el plano inclinado. A menor altura h, menos bolas tiene la cadena en la parte vertical y menor será, por tanto, la energía potencial de la cadena que yace en el plano vertical y viceversa (cadena en equilibrio).

• 

  El sistema mecánico oscilatorio más sencillo: una masa m sujeta a un muelle de constante elástica k. El cuerpo oscila en el eje x.

• 

  El área bajo la recta representa el trabajo realizado por la fuerza.

• 

  James Prescott Joule

• 

  Un bloque se desplaza horizontalmente sujeto a una fuerza de rozamiento, y como consecuencia esta fuerza realiza un trabajo. Como no es conservativa, el trabajo total que realiza en el viaje de ida y vuelta no es nulo, todo lo contrario a lo que ocurriría si la fuerza fuera conservativa.

• 

  Fricción entre dos superficies sólidas

• 

  Ejemplo del trabajo de una fuerza conservativa, el peso, en el viaje de ida y vuelta. Un ascensor con una persona dentro sube y baja. Se considera el trabajo realizado contra la fuerza del peso (de la persona y el ascensor) al subir, sumado al trabajo debido al citado peso al bajar. Como ambos trabajos son exactamente iguales pero de signo contrario, el trabajo total, será cero.

• 

  Ecuación de Bernoulli aplicada a un fluido en una conducción

Véase también

En inglés: Mechanical energy Facts for Kids

• Energía
• Energía potencial
• Energía cinética
• Conservación de la energía
• Energía hidráulica
• Energía eólica
• Ingeniería electromecánica