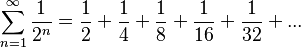Paradojas de Zenón para niños
Las paradojas de Zenón son una serie de problemas filosóficos muy antiguos, creados por el pensador griego Zenón de Elea (alrededor del 490 al 430 a.C.). Zenón las propuso para apoyar la idea de su maestro Parménides, quien creía que el movimiento y la existencia de muchas cosas diferentes eran solo una ilusión de nuestros sentidos. En otras palabras, Parménides pensaba que la realidad era una sola cosa inmutable.
Zenón usó estas paradojas para mostrar que, si creíamos en el movimiento o en la existencia de muchas cosas, llegaríamos a conclusiones muy extrañas y contradictorias.
Contenido
- ¿De dónde vienen las paradojas de Zenón?
- ¿Cómo funcionan las paradojas de Zenón?
- Paradojas del movimiento
- Otras paradojas mencionadas por Aristóteles
- Paradojas de la pluralidad
- Soluciones propuestas
- Las paradojas de Zenón a partir del siglo XIX
- Ideas similares en la antigua China
- Efecto cuántico de Zenón
- Comportamiento de Zenón
- Galería de imágenes
- Véase también
¿De dónde vienen las paradojas de Zenón?

Zenón se interesó mucho en cómo entendemos el continuo (algo que no tiene interrupciones, como una línea sin fin), el espacio, el tiempo y el movimiento. Se dice que creó unas 40 paradojas.
Según el filósofo Platón, Zenón hizo estas paradojas porque otros pensadores habían creado problemas para la visión de Parménides. Así, Zenón quería demostrar que las ideas de sus oponentes llevaban a resultados aún más absurdos. Platón incluso menciona que Sócrates pensaba que Zenón y Parménides defendían la misma idea principal.
De las paradojas de Zenón, solo se conservan nueve, gracias a los escritos de Aristóteles y a los comentarios de Simplicio de Cilicia. Aristóteles intentó refutar algunas de ellas.
Las tres paradojas más famosas y difíciles de explicar son: Aquiles y la tortuga, el argumento de la dicotomía y la de una flecha en vuelo. Las veremos en detalle más adelante.
Los argumentos de Zenón son un ejemplo temprano de un método de prueba llamado "reductio ad absurdum", que significa "reducción al absurdo". Con este método, se asume que algo es cierto para luego demostrar que esa suposición lleva a una contradicción, lo que significa que la suposición original debe ser falsa. También se les considera una base para el método dialéctico que usaba Sócrates.
Algunos expertos, como el matemático Carl Benjamin Boyer, creen que las paradojas de Zenón son solo problemas matemáticos que pueden resolverse con el cálculo infinitesimal moderno. Sin embargo, otros filósofos piensan que estas paradojas siguen siendo importantes para entender la metafísica (la parte de la filosofía que estudia la naturaleza de la realidad).
No se sabe con certeza quién creó estas paradojas. Algunos textos antiguos sugieren que fue Parménides, el maestro de Zenón, quien propuso por primera vez la paradoja de Aquiles y la tortuga, aunque otros atribuyen su origen a Zenón.
¿Cómo funcionan las paradojas de Zenón?
Las paradojas de Zenón suelen empezar asumiendo la idea que quieren refutar. Luego, construyen una cadena de razonamientos que se repite sin fin, lo que se conoce como una regresión infinita. Por ejemplo, en la paradoja de la dicotomía, se divide un camino una y otra vez, argumentando que siempre hay una mitad más que recorrer. Esto se puede repetir infinitamente en la mente, haciendo que parezca imposible llegar al final.
Los argumentos de Zenón giran en torno a si el mundo se puede dividir en partes separadas (unidades discretas) o si es una unidad continua. Si asumimos que todo es divisible, surge el problema de si las cosas se pueden dividir infinitamente o si existen partes mínimas de espacio y tiempo. La mayoría de las paradojas parten de una de estas ideas y concluyen que ciertas cosas que experimentamos como posibles en la vida diaria, como el movimiento, son imposibles.
Algunos creen que Zenón quería defender la idea de su maestro Parménides de que solo existe una realidad infinita y que todo movimiento es una ilusión. Por ejemplo, una persona no podría recorrer una distancia, porque primero tendría que llegar a la mitad, luego a la mitad de esa mitad, y así sucesivamente, sin fin. Esto haría que, en teoría, nunca pudiera empezar o terminar de recorrer la distancia, aunque en la realidad sabemos que sí es posible.
Platón, en su diálogo Parmenides, dice que Zenón intentó proteger a Parménides de las críticas, demostrando que creer en la existencia de muchas cosas y en el movimiento llevaba a conclusiones aún más extrañas.
Zenón mismo dijo que su obra era de juventud y que se había publicado sin su permiso. Lo que sí es seguro es que la filosofía de Zenón se oponía a ciertas ideas comunes sobre cómo funciona el mundo. Sus argumentos nos hacen dudar de nuestras experiencias cotidianas si aceptamos sus premisas.
Con sus paradojas, Zenón nos hace pensar en lo infinitamente pequeño y lo infinitamente grande. Antes de él, se creía que una suma de infinitos números muy pequeños podía crecer sin límite, o que sumar muchos ceros siempre daba cero. Zenón cuestionó la validez de estas ideas.
Las paradojas de Zenón son un tipo de paradojas llamadas "falsídicas" o sofismas. Esto significa que no solo parecen falsas, sino que realmente lo son, porque hay un error en el razonamiento.
Es probable que Zenón no se diera cuenta de las grandes implicaciones que sus ideas tendrían para las matemáticas. Sus paradojas influyeron en el pensamiento matemático durante muchas generaciones, especialmente después del descubrimiento de los números irracionales, lo que llevó a cuestionar si las matemáticas podían ser una ciencia exacta.
Aunque se considera que las paradojas de Zenón han sido refutadas, en el mundo de la física cuántica se confirmó un efecto similar en 1994 en la Universidad de Múnich. Se observó que el movimiento de un sistema cuántico podía detenerse si se medía con mucha frecuencia, lo que llevó a la idea del efecto cuántico de Zenón.
Paradojas del movimiento
¿Puede Aquiles alcanzar a la tortuga?
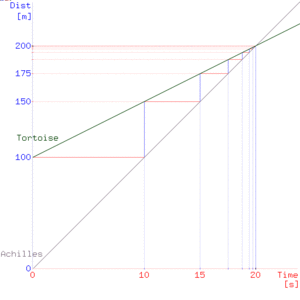
Esta es una de las paradojas más famosas. Imagina que Aquiles, un corredor muy rápido, compite contra una tortuga. Aquiles le da una ventaja a la tortuga, digamos 100 metros.
Zenón argumenta que Aquiles nunca alcanzará a la tortuga. ¿Por qué?
- Primero, Aquiles corre los 100 metros para llegar al punto donde la tortuga empezó.
- Pero mientras Aquiles corre esos 100 metros, la tortuga ya ha avanzado un poco más, digamos 10 metros.
- Ahora, Aquiles tiene que correr esos 10 metros extra.
- Pero mientras Aquiles corre esos 10 metros, la tortuga ha avanzado otro poco, digamos 1 metro.
- Y así sucesivamente. Cada vez que Aquiles llega al punto donde la tortuga estuvo, la tortuga ya se ha movido un poco más.
Parece que Aquiles siempre tendrá una pequeña distancia que recorrer antes de alcanzar a la tortuga.
| Análisis |
|
Aunque parezca lógico, esta situación contradice lo que vemos en la vida real: sabemos que un corredor rápido siempre alcanzará a uno lento, incluso si le da ventaja. Desde el punto de vista matemático, esta paradoja se resuelve con el concepto de serie convergente. Una serie convergente es una suma de infinitos números que se hacen cada vez más pequeños, pero cuya suma total es un número finito. Si sumamos las distancias que Aquiles tiene que recorrer (100 metros + 10 metros + 1 metro + 0.1 metros + ...), obtenemos una serie geométrica que converge a un valor finito. Esto significa que, aunque hay un número infinito de "pasos" o distancias cada vez más pequeñas, el tiempo total que le toma a Aquiles cubrir esas distancias es finito. Por lo tanto, Aquiles sí alcanzará a la tortuga en un momento determinado. Otra forma de verlo es que Aquiles no necesita pensar en infinitas distancias pequeñas. Simplemente corre a una velocidad mayor que la tortuga, y en un tiempo finito, la superará. |
La paradoja de la dicotomía: ¿Puedes empezar a moverte?
Lo que se está moviendo debe llegar a la etapa intermedia antes de llegar a la meta.Según lo contado por Aristóteles, Física VI:9, 239b10
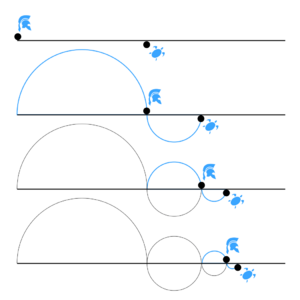
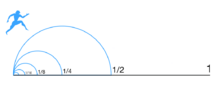
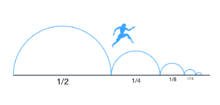
Imagina que quieres caminar hasta el final de un camino. Zenón dice que, antes de llegar al final, debes recorrer la mitad del camino. Y antes de llegar a esa mitad, debes recorrer la mitad de esa mitad (un cuarto del camino). Y antes de eso, la mitad de ese cuarto (un octavo), y así sin parar.

Esta idea sugiere que para moverte, tendrías que completar un número infinito de tareas, lo cual Zenón argumenta que es imposible.
Además, la paradoja plantea que no puede haber una "primera" distancia por recorrer, porque cualquier distancia inicial siempre se podría dividir por la mitad. Así, el viaje no podría ni siquiera empezar. La conclusión paradójica es que el movimiento es una ilusión.
Esta paradoja se llama "dicotomía" porque implica dividir una distancia repetidamente en dos partes. Es similar a la de Aquiles y la tortuga, pero se enfoca más en la imposibilidad de iniciar el movimiento.
| Análisis |
|
Imagina que Zenón está a ocho metros de un árbol y lanza una piedra para golpearlo. Para que la piedra llegue al árbol, primero debe recorrer la mitad de la distancia (cuatro metros). Luego, la mitad de la distancia restante (dos metros), y así sucesivamente. Al igual que en la paradoja de Aquiles y la tortuga, aunque el número de puntos a recorrer sea infinito, la suma de esas distancias es finita. La piedra sí llegará al árbol. Matemáticamente, esto se representa con una serie infinita que suma la mitad, luego la mitad de la mitad, y así hasta el infinito: Esta es una serie geométrica cuya suma es 1. Esto significa que, al sumar todas esas mitades infinitas, se completa la distancia total. Por lo tanto, es posible recorrer toda la distancia, incluso si se divide en infinitas mitades. |
La paradoja de la flecha: ¿Está la flecha realmente en movimiento?
Si todo, cuando ocupa un mismo espacio, está en reposo, y si lo que está en movimiento está ocupando ese mismo espacio en algún momento, entonces la flecha volante permanece inmóvil.según lo contado por Aristóteles, Física VI:9, 239b5
Zenón argumenta que, para que algo se mueva, debe cambiar de posición. Él usa el ejemplo de una flecha en vuelo. Dice que, en cualquier instante de tiempo (un momento tan corto que no tiene duración), la flecha no se está moviendo de donde está ni a donde no está.
- No puede moverse a donde no está, porque no hay tiempo para que se mueva.
- No puede moverse de donde está, porque ya está allí.
En otras palabras, en cada instante, no hay movimiento. Si todo está quieto en cada instante, y el tiempo está hecho de instantes, entonces el movimiento es imposible.
Mientras que las paradojas anteriores dividían el espacio, esta paradoja divide el tiempo en puntos, no en segmentos.
| Análisis |
|
En esta paradoja, una flecha es lanzada. Zenón dice que en cada momento, la flecha está en una posición específica. Si ese momento es muy, muy pequeño, la flecha no tiene tiempo para moverse, así que está en reposo en ese instante. Si esto es cierto para cada instante, entonces la flecha siempre está en reposo, y el movimiento es imposible. Una forma de entender esto es que "estar en reposo" es un concepto relativo. No podemos saber si un objeto está en reposo solo observándolo en un único instante. Necesitamos compararlo con otros instantes cercanos. Si comparamos la posición de la flecha en diferentes instantes, veremos que está en un lugar distinto al que estaba antes y al que estará después. Por lo tanto, la flecha sí se está moviendo. Otra perspectiva es pensar en la definición de velocidad. La velocidad es el cambio de posición en un tiempo determinado. Si un cuerpo se mueve, cambia de lugar en cada momento. El movimiento es la sucesión de las diferentes posiciones que ocupa el cuerpo en los diferentes momentos del tiempo. Si aceptamos que la velocidad y el movimiento pueden definirse de forma lógica, entonces el movimiento existe. |
Otras paradojas mencionadas por Aristóteles
La paradoja del lugar
Aristóteles la describe así:
Si todo lo que existe tiene un lugar, el lugar también tendrá un lugar, y así sucesivamente ad infinitum.
Esta paradoja sugiere que si cada cosa necesita un lugar, entonces el lugar mismo necesitaría un lugar, y así sin fin, lo que llevaría a una cadena infinita de lugares.
La paradoja del grano de mijo
Esta paradoja, según el Diccionario de Filosofía de Routledge, dice:
El argumento es que un solo grano de mijo no emite ningún sonido al caer, pero mil granos sí emiten un sonido. De ahí que mil nadas se conviertan en algo, se considera una conclusión absurda.
Zenón cuestiona cómo algo que no produce sonido por sí solo puede, al unirse con otros iguales, producir un sonido. Aristóteles respondió que incluso los sonidos muy pequeños que no podemos oír pueden sumarse para crear un sonido audible.
Las filas móviles (o el estadio)
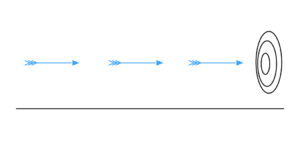
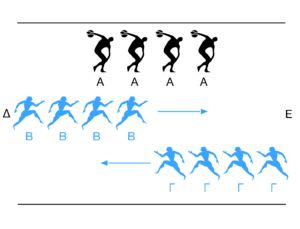
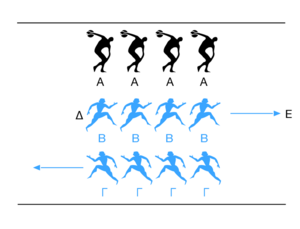
Imagina un estadio con tres filas paralelas de cuatro atletas cada una, separadas por la misma distancia.
- La fila A se queda quieta en el centro del estadio.
- Las filas B y Γ corren a la misma velocidad, pero en direcciones opuestas. La fila B viene de un lado y la fila Γ del otro.
En un momento, llegan a una "situación inicial" donde los corredores de B y Γ están alineados con los de A. Poco después, llegan a una "situación final" donde todos los corredores de B y Γ están alineados con los de A.
Zenón observa que, en el mismo tiempo, los corredores de la fila B se han movido cuatro posiciones respecto a los de la fila Γ, pero solo dos posiciones respecto a los de la fila A (que no se movieron). ¿Cómo es posible que hayan recorrido distancias diferentes en el mismo tiempo?
Según Aristóteles, esta paradoja lleva a la conclusión de que "la mitad de un tiempo dado es igual al doble de ese tiempo", lo cual es una contradicción.
Paradojas de la pluralidad
Además de las paradojas del movimiento, Zenón también planteó paradojas sobre la "pluralidad", es decir, sobre la existencia de muchas cosas diferentes. Estas paradojas son un poco más difíciles de entender hoy en día, ya que los textos antiguos son menos claros.
El argumento de la densidad
Simplicio cita este argumento de Zenón:
Si existe la pluralidad, entonces necesariamente tiene que haber exactamente la cantidad de cosas que hay, ni más, ni menos, pero si hay tantas cosas como hay, entonces están [en cuanto a su número] limitadas.
Si existe la pluralidad, entonces el ser [en cuanto a su número] es ilimitado. Porque entre las cosas individuales siempre hay otras cosas y entre ellas a su vez, nuevamente otras. Así, el ser es ilimitado.Simpl., Phys, 140 (29), en: Die Fragmente der Vorsokratiker. Edición en griego y alemán por Hermann Diels. Vol. I, Berlín 1922, p. 173–175.
La idea es que si hay muchas cosas, deben estar separadas. Pero si están separadas, debe haber "algo" entre ellas. Y entre ese "algo" y las cosas originales, debe haber más "algo", y así hasta el infinito. Esto lleva a una contradicción: si hay muchas cosas, su número debe ser limitado, pero al mismo tiempo, parece que su número es ilimitado.
El argumento del tamaño finito
Este argumento también fue transmitido por Simplicio. Zenón parece decir que si hay muchas cosas, cada una debe tener un tamaño. Pero si algo no tiene tamaño, es nada. Luego, si un objeto tiene tamaño, y hay muchos, entonces deben ser infinitos objetos finitos, porque siempre hay algo que los delimita.
Si la hay [la pluralidad], entonces cada una de sus partes individuales tiene que tener un tamaño, un grosor y una separación de otros objetos determinados. Y lo mismo se puede decir de las partes que se encuentran antes que estas. Por supuesto, también tendrán tamaño y habrá otra parte a su lado. Lo mismo es verdad una vez y todas las veces. Porque ninguna parte de lo mismo formará el límite final, y nunca una no estará relacionada con otra. Entonces, si hay muchas cosas, necesariamente deben ser pequeñas y grandes: la nada o grandes hasta el infinito.Simpl., Phys, 140 (34), De: Los fragmentos de los presocráticos. Griego y alemán por Hermann Diels. 1. Band, Berlín 1922, S. 173–175.
Este argumento es complejo, pero una interpretación es que si las cosas son distintas, deben estar separadas. Y si están separadas, debe haber algo entre ellas, lo que lleva a una cadena infinita de divisiones.
Soluciones propuestas
Diógenes el Cínico
Se cuenta que Diógenes de Sinope, al escuchar los argumentos de Zenón, no dijo nada. Simplemente se levantó y caminó para demostrar que las conclusiones de Zenón eran falsas. Esto se conoce como "solvitur ambulando" (se resuelve caminando). Sin embargo, para resolver una paradoja por completo, no basta con demostrar que la conclusión es falsa; hay que explicar dónde está el error en el razonamiento.
Aristóteles
Aristóteles (384 a.C. − 322 a.C.) notó que a medida que la distancia disminuye, el tiempo necesario para cubrirla también disminuye. Así, el tiempo también se vuelve cada vez más pequeño.
También diferenció entre cosas que son "infinitas en divisibilidad" (como una línea que se puede dividir mentalmente en partes cada vez más pequeñas) y cosas que son "infinitas en extensión" (como una línea que se extiende sin fin). La objeción de Aristóteles a la paradoja de la flecha fue que "el tiempo no está hecho de puntos indivisibles, así como ninguna otra magnitud está hecha de indivisibles".
Tomás de Aquino
Tomás de Aquino, comentando a Aristóteles, escribió que "los instantes no son partes del tiempo". Esto significa que el tiempo no está compuesto de momentos sin duración, de la misma manera que una línea no está hecha de puntos.
Arquímedes
Antes del 212 a.C., Arquímedes desarrolló un método para encontrar una suma finita para una serie infinita de términos que se hacen cada vez más pequeños. Esto es lo que hoy conocemos como serie geométrica convergente. El cálculo moderno usa métodos más precisos para llegar al mismo resultado. Estos métodos demuestran que, aunque los pasos de Zenón son infinitos, el tiempo total para completarlos es finito.
Bertrand Russell
Bertrand Russell propuso la "teoría de movimiento de-de". Él estuvo de acuerdo en que no puede haber movimiento "durante" un instante sin duración. Pero argumentó que para que haya movimiento, la flecha solo necesita estar en un punto en un momento, en otro punto en otro momento, y en los puntos intermedios en los tiempos intermedios. Desde este punto de vista, el movimiento es una relación entre la posición y el tiempo.
Peter Lynds
Peter Lynds ha argumentado que las paradojas del movimiento de Zenón se resuelven al entender que los instantes de tiempo y las magnitudes instantáneas no existen físicamente. Él dice que un objeto en movimiento no puede tener una posición instantánea o definida, porque si la tuviera, no podría estar en movimiento. Por lo tanto, su movimiento no puede dividirse en fracciones como suponen las paradojas.
Hermann Weyl
Otra solución es cuestionar una de las suposiciones de Zenón (especialmente en la dicotomía): que entre dos puntos diferentes en el espacio (o tiempo), siempre hay otro punto. Si no se asume esto, solo habría un número finito de distancias entre dos puntos, y no una secuencia infinita de movimientos, lo que resolvería la paradoja. Las ideas de longitud de Planck y tiempo de Planck en la física moderna sugieren que hay límites mínimos para la medición del tiempo y el espacio.
Las paradojas de Zenón a partir del siglo XIX
Los procesos infinitos siguieron siendo un desafío en matemáticas hasta finales del siglo XIX. Matemáticos como Weierstrass y Cauchy desarrollaron formas rigurosas de entender el cálculo y las series infinitas. Estos trabajos dieron una base sólida a las matemáticas que involucran procesos infinitos.
Aunque las matemáticas pueden calcular dónde y cuándo Aquiles superará a la tortuga, algunos filósofos argumentan que las matemáticas no abordan el punto central de Zenón y que resolver los problemas matemáticos no resuelve todos los problemas filosóficos que plantean las paradojas.
A veces, la gente malinterpreta los argumentos de Zenón, diciendo que él argumentó que la suma de un número infinito de términos debe ser infinita. Sin embargo, las fuentes antiguas no muestran a Zenón discutiendo la suma de series infinitas. Simplicio dice que Zenón afirmó que "es imposible atravesar un número infinito de cosas en un tiempo finito". El problema de Zenón no era encontrar la suma, sino "terminar" una tarea con un número infinito de pasos.
El debate sobre si las paradojas de Zenón se han resuelto o no continúa. Algunos historiadores de las matemáticas creen que la noción de una "serie infinita convergente" ofrece una explicación satisfactoria.
Bertrand Russell propuso una "solución" basada en el trabajo de Georg Cantor, pero algunos piensan que las paradojas de Zenón, por su simplicidad, siempre servirán como una especie de "test de Rorschach" donde las personas pueden proyectar sus preocupaciones más profundas sobre la realidad.
Ideas similares en la antigua China
Los filósofos de la Antigua China de la Escuela de los Nombres, durante el período de los Reinos combatientes (479-221 a.C.), desarrollaron ideas similares a algunas de las paradojas de Zenón de forma independiente. El historiador Joseph Needham describe una paradoja china antigua que dice que "un palo de un pie, todos los días quita la mitad, y en innumerables edades no se agotará". Esto es muy parecido a la paradoja de la dicotomía.
Efecto cuántico de Zenón
En 1977, los físicos George Sudarshan y B. Misra descubrieron que el movimiento de un sistema cuántico puede ser frenado o incluso detenido si se observa constantemente. Este efecto se llama "efecto cuántico de Zenón" porque recuerda mucho a la paradoja de la flecha de Zenón. La idea de este efecto se propuso por primera vez en 1958.
Comportamiento de Zenón
En el diseño de sistemas complejos, se dice que un sistema tiene un "comportamiento de Zenón" si realiza un número infinito de pasos discretos en un tiempo finito. A menudo, estos comportamientos se evitan en los modelos de sistemas, ya que no se pueden implementar con controladores digitales.
Galería de imágenes
Véase también
 En inglés: Zeno's paradoxes Facts for Kids
En inglés: Zeno's paradoxes Facts for Kids
- Aporía
- Experimento mental
- Filosofía del espacio y el tiempo
- Supertarea
- "Lo que la tortuga le dijo a Aquiles", un diálogo alegórico sobre los fundamentos de la lógica de Lewis Carroll (1895).
- Máquina de Zenón