Mathematica para niños
Datos para niños Wolfram Mathematica |
|||
|---|---|---|---|
 |
|||
 |
|||
| Información general | |||
| Tipo de programa | lenguaje de programación | ||
| Autor | Stephen Wolfram | ||
| Desarrollador | Wolfram Research | ||
| Modelo de desarrollo | Software propietario | ||
| Lanzamiento inicial | 23/06/1988 | ||
| Licencia | Software propietario | ||
| Idiomas | Inglés, español, chino, japonés | ||
| Información técnica | |||
| Programado en | |||
| Interfaz gráfica predeterminada | Qt | ||
| Versiones | |||
| Última versión estable | 14.223 de enero de 2025 | ||
| Archivos legibles | |||
|
|||
| Archivos editables | |||
|
|||
| Enlaces | |||
|
Sitio web oficial
|
|||
Mathematica es un programa de computadora muy potente. Se usa en campos como la ciencia, la ingeniería y las matemáticas. Fue creado por Stephen Wolfram, quien aún dirige al equipo que lo desarrolla en la empresa Wolfram Research. Mathematica es conocido por resolver problemas matemáticos complejos y también es un lenguaje de programación muy completo.
Contenido
¿Qué es Mathematica y cómo funciona?
La primera versión de Mathematica se lanzó en 1988. Hoy en día, está disponible para muchos tipos de computadoras.
Mathematica tiene dos partes principales:
- El núcleo (o kernel): Es el "cerebro" del programa. Aquí se hacen todos los cálculos y se interpretan las instrucciones que le das.
- La interfaz: Es la parte que ves en la pantalla. Te permite escribir las instrucciones, ver los resultados, crear gráficos y organizar tu trabajo como si fuera un cuaderno digital. Puedes combinar texto, código, imágenes y gráficos en un mismo documento.
Los archivos de Mathematica suelen terminar en .nb (para los cuadernos) o .m (para configuraciones).
¿Para qué sirve Mathematica?
Mathematica es como una navaja suiza para las matemáticas y la computación. Puede hacer muchas cosas, como:
- Realizar cálculos matemáticos muy avanzados.
- Trabajar con matrices y grandes cantidades de datos.
- Manejar números complejos y cálculos con mucha precisión.
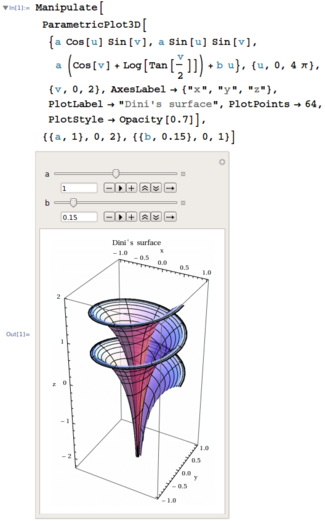
- Crear gráficos en 2D y 3D, animaciones y mapas.
- Resolver diferentes tipos de ecuaciones.
- Hacer cálculos de Estadística y probabilidad.
- Ayudar con el aprendizaje de máquina (inteligencia artificial).
- Analizar formas geométricas en 2D y 3D.
- Optimizar problemas para encontrar la mejor solución.
- Procesar imágenes y reconocer elementos en ellas.
- Analizar redes y conexiones (grafos).
- Buscar patrones en textos y datos.
- Hacer cálculos financieros.
- Procesar señales (como sonidos o imágenes).
- Conectarse a bases de datos y servicios en línea como WolframAlpha.
- Crear documentos técnicos con fórmulas y reportes.
Conexiones con otros programas
Mathematica puede comunicarse con otros programas usando un sistema llamado MathLink. Esto permite que el programa se conecte con aplicaciones hechas en lenguajes como Java o .NET. Así, otros programas pueden pedirle a Mathematica que haga cálculos o Mathematica puede usar funciones de esos programas.
Mathematica funciona en sistemas operativos como Linux, macOS de Apple y Windows. También es compatible con computadoras pequeñas como la Raspberry Pi.
Además, Mathematica puede conectarse a muchos servicios en internet para obtener o enviar información. Algunos ejemplos son ArXiv, Dropbox, Facebook, Flickr, Google, Instagram, LinkedIn, Reddit, Twitter y Wikipedia.
Mathematica en Internet
Wolfram Research tiene un programa llamado webMathematica. Este programa permite que los cálculos y gráficos de Mathematica se puedan ver y usar directamente en páginas web.
Para que la gente vea lo que Mathematica puede hacer, Wolfram Research tiene sitios web donde puedes probar algunas de sus funciones. Por ejemplo, tienen una calculadora de integrales y un proyecto llamado "Demonstrations project". Este proyecto tiene muchos programas pequeños que muestran conceptos matemáticos o funciones de Mathematica de forma visual y sencilla. Puedes verlos en tu navegador o con un programa gratuito llamado Mathematica Player.
Ejemplos de uso
Aquí te mostramos cómo se usa Mathematica con algunos ejemplos sencillos:
Calcular el determinante de una matriz
Imagina que quieres calcular el determinante de una matriz (una tabla de números) de 6x6. Si los números son el resultado de multiplicar su posición (fila x columna) y los ceros se cambian por 1, Mathematica lo hace así:
In[1]:= Det[Array[Times, {6, 6}, 0] /. 0 -> 1] Out[1]= 0
El resultado es 0.
Encontrar la raíz de una ecuación
Si necesitas encontrar un valor de x que resuelva la ecuación ex = x2 + 2, empezando la búsqueda cerca de x = -1, Mathematica te da la respuesta:
In[2]:= FindRoot[Exp[x] == x^2 + 2, {x, -1}] Out[2]= {x -> 1.3190736768573652}
El valor de x es aproximadamente 1.319.
Diferentes formas de programar
Mathematica te permite programar de varias maneras. Por ejemplo, para crear una tabla con el máximo común divisor (GCD) de números del 1 al 5:
Puedes usar una función especial: In[3]:= Array[GCD, {5, 5}] Out[3]= {{1, 1, 1, 1, 1}, {1, 2, 1, 2, 1}, {1, 1, 3, 1, 1}, {1, 2, 1, 4, 1}, {1, 1, 1, 1, 5}}
O de esta otra forma: In[4]:= Table[GCD[x, y], {x, 1, 5}, {y, 1, 5}] Out[4]= {{1, 1, 1, 1, 1}, {1, 2, 1, 2, 1}, {1, 1, 3, 1, 1}, {1, 2, 1, 4, 1}, {1, 1, 1, 1, 5}}
También puedes hacerlo paso a paso (de forma iterativa), aunque es más largo: In[6]:= l1 = {}; (* inicia una lista vacía *) For[i = 1, i <= 5, i++, l2 = {}; For[j = 1, j <= 5, j++, l2 = Append[l2, GCD[i, j] ] ]; l1 = Append[l1, l2]; (* añade la fila a la lista principal *) ]; l1 Out[6]= {{1, 1, 1, 1, 1}, {1, 2, 1, 2, 1}, {1, 1, 3, 1, 1}, {1, 2, 1, 4, 1}, {1, 1, 1, 1, 5}}
Historia de las versiones
Mathematica se basó en un trabajo anterior llamado Symbolic Manipulation Program (SMP). El nombre "Mathematica" fue sugerido por Steve Jobs, cofundador de Apple, aunque Stephen Wolfram ya lo había considerado.
Wolfram Research ha lanzado muchas versiones de Mathematica a lo largo de los años. La primera fue en 1988. La versión más reciente es la 14.1, lanzada el 31 de julio de 2024.
Galería de imágenes
Véase también
- Software matemático
- Wolfram Alpha
- Wolfram (lenguaje de programación)