Masa terrestre para niños
La masa terrestre o masa de la Tierra (M🜨) es una unidad de medida que se usa en la astronomía y la astrofísica. Sirve para comparar el tamaño de la masa de los planetas, exoplanetas (planetas fuera de nuestro sistema solar) y otros objetos celestes más pequeños, como los asteroides o planetas enanos.
La masa de la Tierra es de aproximadamente 5,97 x 1024 kilogramos (kg). Esto es casi 6 cuatrillones de kilos, o 6 mil trillones de toneladas. ¡Es una cantidad enorme!
Los científicos calculan la masa de la Tierra usando información muy precisa sobre la constante geocéntrica (GM), que se obtiene con la geodesia espacial (el estudio de la forma y el campo gravitatorio de la Tierra). También usan la constante de gravitación universal (G) de Isaac Newton, aunque esta última es un poco más difícil de medir con total exactitud.
La masa de la Tierra se usa mucho para describir el tamaño de los planetas rocosos o terrestres. En nuestro sistema solar, además de la Tierra, hay otros tres planetas rocosos: Mercurio, Venus y Marte. Sus masas son:
- Mercurio: 0.055 veces la masa de la Tierra.
- Venus: 0.815 veces la masa de la Tierra.
- Marte: 0.107 veces la masa de la Tierra.
Contenido
Comparación de la masa terrestre con otros cuerpos celestes
La masa de la Tierra se puede comparar con la de muchos otros cuerpos celestes. Aquí te mostramos algunas equivalencias:
- Es 81.3 veces la masa de la Luna.
- Es 0.00315 veces la masa de Júpiter. Esto significa que Júpiter es 317.83 veces más masivo que la Tierra.
- Es 0.0105 veces la masa de Saturno. Saturno es 95.16 veces más masivo que la Tierra.
- Es 0.0583 veces la masa de Neptuno. Neptuno es 17.15 veces más masivo que la Tierra.
- Es 0.000 003 003 veces la masa solar. El Sol es 332 946 veces más masivo que la Tierra.
Cómo se ha medido la masa de la Tierra
Desde el siglo XVII, los científicos han buscado formas de medir la masa de la Tierra con precisión. Gran parte de esta historia está ligada a la geodesia (el estudio de la forma de la Tierra) y a la historia de la física, especialmente a los experimentos para determinar la constante de gravitación universal (G), que comenzaron a finales del siglo XVIII con Henry Cavendish.
Usando las leyes de Kepler
Una forma de calcular la masa de la Tierra es usando la tercera ley de Kepler. Esta ley describe cómo se mueven los planetas alrededor del Sol, y también cómo se mueven los satélites (naturales o artificiales) alrededor de un planeta.
Si un satélite gira alrededor de la Tierra, podemos usar su órbita (su distancia y el tiempo que tarda en dar una vuelta) para calcular el producto de la constante de gravitación (G) por la masa de la Tierra (M). Este valor se conoce como la "constante gravitacional geocéntrica".
Al principio, se usó la Luna para estos cálculos, pero su órbita es compleja. Con la llegada de los satélites artificiales en 1957, las mediciones se hicieron mucho más precisas.
Usando péndulos
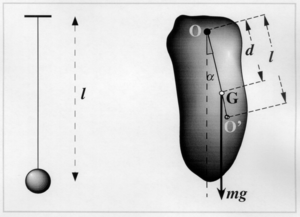
También se puede determinar la masa de la Tierra midiendo cómo se comportan los péndulos. Si imaginamos que la Tierra es una esfera perfecta y no gira, la fuerza de la gravedad (que hace que las cosas caigan) en su superficie depende de la masa de la Tierra y de su radio.
Un péndulo simple (como una cuerda con una pesa que se balancea) tiene un período de oscilación (el tiempo que tarda en ir y volver) que depende de su longitud y de la fuerza de la gravedad. Midiendo la longitud del péndulo y su período, se puede calcular la fuerza de la gravedad y, a partir de ahí, la masa de la Tierra.
Científicos como Jean Richer y Christiaan Huygens hicieron experimentos con péndulos en el siglo XVII. Richer descubrió en 1672 que un péndulo que marcaba los segundos exactos en París se atrasaba en Cayenne (cerca del ecuador). Esto ayudó a confirmar que la Tierra no es una esfera perfecta, sino que está un poco achatada por los polos, y que la gravedad es ligeramente menor en el ecuador.
Ideas de Isaac Newton
Isaac Newton propuso dos formas de medir la constante de gravitación (G) o la masa de la Tierra (M) por separado:
- Medir la fuerza de atracción entre dos objetos de masa conocida en un laboratorio. Esto permitiría calcular G.
- Medir cuánto se desvía una plomada (una cuerda con una pesa que cuelga verticalmente) cerca de una montaña. La montaña, al tener masa, atraería la plomada, desviándola un poco. Si se conociera la masa de la montaña, se podría estimar la masa de la Tierra.
Los primeros intentos de usar el segundo método fueron de Pierre Bouguer en el Ecuador (1735-1744). El primer experimento para medir G en un laboratorio fue realizado con éxito por Henry Cavendish en 1798.
Newton pensaba que la atracción entre objetos pequeños sería tan débil que sería muy difícil de medir. Sin embargo, sus ideas sentaron las bases para futuros experimentos.
Masa de la Tierra a partir de desviaciones de la vertical
Este método consiste en observar cómo una montaña grande desvía la dirección de una plomada.
El experimento de Bouguer en el Chimborazo
Durante una expedición al Ecuador, Pierre Bouguer intentó determinar la densidad media de la Tierra (y por lo tanto su masa) en 1738. Eligió el volcán Chimborazo, una montaña alta y con una forma bastante regular.
Bouguer midió la desviación de una plomada causada por la atracción de la montaña. Aunque sus mediciones no fueron muy precisas, demostraron que la Tierra no estaba hueca o llena de agua, como algunos pensaban en ese momento. Sus experimentos sirvieron de base para futuras investigaciones.
Experimento de Maskelyne en el monte Schiehallion
En 1772, el astrónomo Nevil Maskelyne propuso repetir el experimento de Bouguer. Se eligió el Monte Schiehallion en Escocia. Entre 1774 y 1776, Maskelyne y su equipo realizaron mediciones muy cuidadosas.
Los cálculos, en los que participaron el geólogo James Hutton y el físico Henry Cavendish, permitieron estimar la densidad media de la Tierra en aproximadamente 4.5 gramos por centímetro cúbico (g/cm³). Con el tiempo, esta estimación se fue refinando, llegando a 4.95 g/cm³ en 1821.
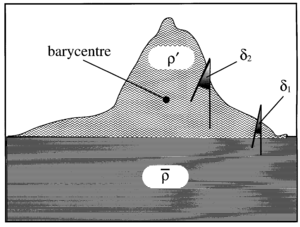
Isostasia y límites del método
Los experimentos de desviación de la plomada mostraron que era difícil determinar la masa de la Tierra con mucha precisión usando este método. Esto se debe a un fenómeno llamado isostasia. La isostasia es un equilibrio en la corteza terrestre donde las montañas grandes tienen raíces más profundas y menos densas que "flotan" en el manto, compensando su peso. Esto hace que la atracción gravitatoria de las montañas sea menor de lo esperado.
El experimento de Cavendish
El segundo método sugerido por Newton para determinar la masa de la Tierra fue medir directamente la constante de gravitación universal (G) en un laboratorio.
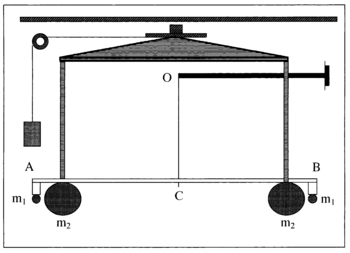
A finales del siglo XVIII, John Michell diseñó un aparato llamado balanza de torsión. Este aparato podía medir la fuerza de atracción muy pequeña entre dos esferas de plomo. La ley de gravitación de Newton dice que la fuerza de atracción entre dos objetos depende de sus masas y de la distancia entre ellos, y de la constante G.
Michell murió antes de poder usar su invento, y el aparato llegó a manos de Henry Cavendish. Cavendish hizo algunas mejoras y en 1798 publicó sus resultados. Midiendo la fuerza de atracción entre las esferas, Cavendish pudo calcular el valor de G. Con este valor y la fuerza de la gravedad en la superficie de la Tierra, pudo determinar la densidad media de la Tierra en 5.448 g/cm³.
Experiencias similares a la de Cavendish
Después de Cavendish, muchos otros científicos realizaron experimentos similares para medir G con mayor precisión:
- Ferdinand Reich (1837, 1852)
- Francis Baily (1842)
- Marie Alfred Cornu y Jean-Baptistin Baille (1873)
- Philipp von Jolly (1881)
- John Henry Poynting (1892)
- Charles Vernon Boys (1895), quien mejoró el aparato usando un hilo de cuarzo.
- Karl Ferdinand Braun y Eötvös Loránd (1896), quienes diseñaron una balanza de torsión muy sensible.
Estos experimentos fueron refinando el valor de la densidad media de la Tierra, acercándose cada vez más al valor actual.
Los valores de G más aceptados hoy en día provienen de experimentos más recientes, como los de Paul Renno Heyl (1930) y P. R. Heyl y Peter Chrzanowski (1942).
Actualmente, el producto de G por la masa de la Tierra (GM) se conoce con mucha precisión gracias a los satélites artificiales. Sin embargo, el valor de G por sí solo, y por lo tanto la masa de la Tierra (M), todavía tienen una pequeña incertidumbre. Los científicos siguen realizando experimentos para medir G con la mayor exactitud posible.
Véase también
 En inglés: Earth mass Facts for Kids
En inglés: Earth mass Facts for Kids
- Órdenes de magnitud (masa)
- Planeta terrestre
- Experimento de Cavendish
- Radio terrestre