Límite de Roche para niños
En astronomía, el límite de Roche es la distancia mínima a la que un objeto, como una luna o un cometa, puede orbitar alrededor de un cuerpo más grande, como un planeta, sin que las fuerzas de marea de ese planeta lo rompan. Imagina que un objeto se mantiene unido por su propia gravedad. Si se acerca demasiado a un planeta muy grande, la fuerza de gravedad del planeta será mucho más fuerte en el lado del objeto que está más cerca del planeta que en el lado más lejano. Esta diferencia de fuerza se llama fuerza de marea.
Dentro del límite de Roche, la fuerza de marea del planeta es tan fuerte que supera la propia gravedad del objeto, haciendo que este se desintegre. El astrónomo francés Édouard Roche fue el primero en describir este efecto y calcular esta distancia en 1848.
El límite de Roche depende de la gravedad del cuerpo central (el planeta) y también de la densidad del objeto que lo orbita (la luna o cometa).
Es importante no confundir el límite de Roche con el lóbulo de Roche. El lóbulo de Roche es otra idea de Édouard Roche que describe el espacio donde un objeto pequeño es atraído por uno de dos cuerpos grandes en un sistema.
Algunos objetos, tanto naturales como hechos por el hombre, pueden orbitar más cerca que el límite de Roche. Esto ocurre porque no solo se mantienen unidos por su gravedad, sino también por la resistencia de su material. Por ejemplo, algunas lunas de Júpiter, como Adrastea y Metis, están dentro de sus límites de Roche. Sin embargo, cualquier cosa suelta en su superficie podría ser arrancada por las fuerzas de marea. Un objeto menos resistente, como un cometa, se romperá al cruzar su límite de Roche. El cometa Shoemaker-Levy 9 se rompió en muchos pedazos al pasar el límite de Roche de Júpiter en 1992. Dos años después, en 1994, esos pedazos chocaron contra el planeta.
Dentro del límite de Roche, las fuerzas de marea son tan grandes que las partículas pequeñas no pueden unirse para formar un objeto más grande. Por eso, todos los anillos planetarios (como los de Saturno) se encuentran dentro de sus límites de Roche. Estos anillos podrían ser restos de material que nunca logró formar una luna, o podrían ser los restos de una luna que se rompió al cruzar el límite de Roche.
El límite de Roche se calcula principalmente por las fuerzas de gravedad y marea. Sin embargo, en la realidad, la estabilidad de una luna también depende de qué tan rápido gira y de la fuerza que la empuja hacia afuera debido a esa rotación (fuerza centrífuga).
Contenido
¿Cómo se calcula el límite de Roche?
El cálculo del límite de Roche varía un poco dependiendo de si el objeto que orbita es un cuerpo sólido y rígido o si es un cuerpo que puede deformarse fácilmente, como si fuera líquido.
Para cuerpos rígidos
Si el objeto es una esfera perfecta y sólida, el límite de Roche se calcula con esta fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d = R\left( 2\;\frac {\rho_M} {\rho_m} \right)^{\frac{1}{3}}
Donde:
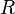 es el radio del cuerpo principal (el planeta).
es el radio del cuerpo principal (el planeta).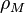 es la densidad del cuerpo principal.
es la densidad del cuerpo principal.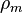 es la densidad del objeto que orbita (la luna o cometa).
es la densidad del objeto que orbita (la luna o cometa).
Si la luna es más de dos veces más densa que el planeta, el límite de Roche estaría dentro del propio planeta, lo que significa que no es una distancia relevante para que la luna se rompa.
Para cuerpos deformables
Si el objeto puede cambiar de forma fácilmente, como un líquido, el cálculo es un poco diferente. Una buena aproximación para este caso es:
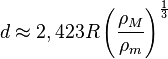
Esta fórmula es un poco más grande que la de los cuerpos rígidos, lo que significa que un objeto deformable se romperá a una distancia mayor.
Ejemplos del límite de Roche en nuestro Sistema Solar
Para entender mejor el límite de Roche, veamos algunos ejemplos con los cuerpos de nuestro sistema solar. La siguiente tabla muestra la densidad y el radio de algunos de ellos:
| Cuerpo | Densidad (kg/m³) | Radio (m) |
|---|---|---|
| Sol | 1.400 | 695.000.000 |
| Júpiter | 1.330 | 71.500.000 |
| Tierra | 5.515 | 6.376.500 |
| Luna | 3.340 | 1.737.400 |
La densidad promedio de los cometas es de unos 500 kg/m³.
El límite de Roche real de un objeto estará entre los valores calculados para un cuerpo rígido y uno deformable, ya que la mayoría de los objetos no son ni perfectamente rígidos ni perfectamente líquidos. Si el planeta es menos denso que la mitad del objeto que lo orbita, el límite de Roche puede estar dentro del planeta, lo que significa que el objeto no puede alcanzar esa distancia sin chocar. Esto sucede, por ejemplo, con el sistema Sol-Tierra.
La siguiente tabla muestra los límites de Roche para algunos pares de cuerpos, tanto para objetos rígidos como para los que se deforman:
| Cuerpo | Satélite | Límite de Roche (rígido) | Límite de Roche (no rígido) | ||
|---|---|---|---|---|---|
| Distancia (m) | Radio | Distancia (m) | Radio | ||
| Tierra | Luna | 9.495.665 | 1,49 | 18.261.459 | 2,86 |
| Tierra | Cometa | 17.883.432 | 2,80 | 34.392.279 | 5,39 |
| Sol | Tierra | 554.441.389 | 0,80 | 1.066.266.402 | 1,53 |
| Sol | Cometa | 1.234.186.562 | 1,78 | 2.373.509.071 | 3,42 |
Es interesante ver qué tan cerca o lejos están las lunas de nuestro sistema solar de sus límites de Roche. La siguiente tabla compara el radio orbital de cada luna con sus límites de Roche (rígido y no rígido). Para los planetas gigantes, solo se incluyen las lunas interiores más pequeñas, ya que las lunas grandes como Ío (de Júpiter) o Titán (de Saturno) están mucho más lejos de sus límites de Roche.
| Cuerpo central | Satélite | Radio Orbital: Límite de Roche | |
|---|---|---|---|
| (Rígido) | (No Rígido) | ||
| Sol | Mercurio | 104:1 | 54:1 |
| Tierra | Luna | 41:1 | 21:1 |
| Marte | Fobos | 171% | 89% |
| Deimos | 456% | 237% | |
| Júpiter | Metis | 191% | 99% |
| Adrastea | 192% | 100% | |
| Amaltea | 178% | 93% | |
| Tebe | 331% | 172% | |
| Saturno | Pan | 177% | 92% |
| Atlas | 182% | 95% | |
| Prometeo | 185% | 96% | |
| Pandora | 188% | 98% | |
| Epimeteo | 198% | 103% | |
| Urano | Cordelia | 155% | 81% |
| Ofelia | 168% | 87% | |
| Bianca | 184% | 96% | |
| Crésida | 193% | 100% | |
| Neptuno | Náyade | 144% | 75% |
| Talasa | 149% | 78% | |
| Despina | 157% | 82% | |
| Galatea | 184% | 96% | |
| Larisa | 219% | 114% | |
| Plutón | Caronte | 13:1 | 6,8:1 |
Es notable que las lunas más pequeñas de los planetas gigantes están muy cerca de sus límites de Roche. Esto significa que su estructura se mantiene por la fuerza de sus materiales, no solo por su propia gravedad. En las regiones donde hay anillos, como los anillos de Saturno, las partículas no pueden unirse para formar objetos más grandes porque las fuerzas de marea las separarían. Estas lunas probablemente se formaron más lejos de los planetas y luego sus órbitas cambiaron, o se formaron cerca cuando los planetas aún eran más pequeños.
Galería de imágenes
Véase también
 En inglés: Roche limit Facts for Kids
En inglés: Roche limit Facts for Kids
- Esfera de Hill
- Lóbulo de Roche
- Puntos de Lagrange


