Magnitud adimensional para niños

Enciclopedia para niños

Una magnitud adimensional es una cantidad que no tiene una dimensión física asociada. Imagina que es un número "puro", sin unidades como metros, segundos o kilogramos. Por ejemplo, el número π (pi), que es aproximadamente 3.14159, es un número adimensional. No lo medimos en centímetros ni en litros; es solo un valor.

Estas magnitudes son muy útiles en matemáticas, física, ingeniería y hasta en la vida diaria, como cuando contamos objetos. A diferencia de las magnitudes que sí tienen dimensiones (como la longitud, que se mide en metros, o el tiempo, que se mide en segundos), las magnitudes adimensionales no necesitan una unidad específica.

A menudo, una magnitud adimensional se forma al dividir dos cantidades que sí tienen dimensiones, pero cuyas unidades se cancelan entre sí. Por ejemplo, si mides cuánto se estira un objeto y lo divides por su longitud original, ambas medidas están en unidades de longitud (como centímetros). Al dividirlas, los centímetros se cancelan, y el resultado es un número adimensional que te dice la "deformación relativa" del objeto.

El análisis dimensional es una herramienta que nos ayuda a identificar y trabajar con estas cantidades adimensionales. En el Sistema Internacional de Unidades (SI), la unidad asociada a una magnitud adimensional es simplemente el número 1.

Las magnitudes adimensionales son especialmente importantes en el estudio de los fluidos (como el agua o el aire) y en cómo se mueven el calor o las sustancias. Nos permiten comparar diferentes situaciones o modelos a escala reducida, como los que se usan para diseñar aviones o barcos. A estas magnitudes también se les llama a menudo "números adimensionales" o "números característicos".

Contenido

¿Qué características tienen las magnitudes adimensionales?
¿Cómo nos ayuda el Teorema π de Buckingham?
¿Existen constantes físicas adimensionales?
Lista de magnitudes adimensionales comunes
Véase también

¿Qué características tienen las magnitudes adimensionales?

Aunque una magnitud adimensional no tiene una dimensión física, a veces se le pueden asignar "unidades adimensionales" para aclarar qué se está midiendo. Por ejemplo, si hablamos de la cantidad de sal en una solución, podríamos decir "gramos de sal por gramo de solución" (g/g). Aunque las unidades se cancelan, nos ayuda a entender que es una proporción.

Otras unidades adimensionales comunes son:

El porcentaje (%), que significa "por cada 100". Por ejemplo, 10% es lo mismo que 0.1.
El por mil (‰), que significa "por cada 1000".
Las partes por millón (ppm), que son 10^-6 (una millonésima parte).
Las partes por billón (ppb), que son 10^-9 (una milmillonésima parte).
Las unidades para medir ángulos, como los radianes o los grados.

Aquí tienes algunos ejemplos sencillos:

Manzanas podridas: Si tienes 10 manzanas y 1 está podrida, la relación de manzanas podridas a manzanas totales es (1 manzana) / (10 manzanas) = 0.1. Este 0.1 es un número adimensional, que también puedes expresar como 10%.
Ángulos: Un ángulo se mide comparando la longitud de un arco de círculo con el radio de ese círculo. Como ambas son longitudes, sus unidades se cancelan, y el resultado es un número adimensional. Cuando usamos radianes, comparamos la longitud del arco con el radio.
El número pi (π): Este famoso número es la relación entre la circunferencia de un círculo y su diámetro. No importa si mides el círculo en centímetros, metros o kilómetros; la relación siempre será el mismo número adimensional: aproximadamente 3.14159.

¿Cómo nos ayuda el Teorema π de Buckingham?

El teorema π de Buckingham es una idea muy importante en física. Dice que si tienes una ley física que describe cómo se relacionan varias cantidades, puedes reescribir esa ley usando solo combinaciones adimensionales de esas cantidades.

Esto es fundamental porque las leyes de la física deben ser las mismas sin importar qué sistema de unidades uses (por ejemplo, si usas metros y segundos o pies y libras). Si una ley dependiera de las unidades, ¡sería muy confuso! El teorema π de Buckingham nos asegura que las relaciones importantes en la física se pueden expresar de una manera que no depende de las unidades.

Por ejemplo, imagina que quieres saber cuánta potencia consume un agitador (como el de una batidora). Esa potencia depende de varias cosas: la densidad y la viscosidad del líquido, el tamaño del agitador y la velocidad a la que gira. Según el teorema π de Buckingham, podemos combinar estas cinco variables (potencia, densidad, viscosidad, tamaño, velocidad) en solo dos números adimensionales que nos darán la misma información, sin importar las unidades que usemos para medir cada cosa. Estos dos números son el Número de Reynolds y el Número de potencia.

¿Existen constantes físicas adimensionales?

Sí, algunas constantes físicas fundamentales son adimensionales. Esto significa que su valor es siempre el mismo, sin importar el sistema de unidades que elijas. Estas constantes se determinan mediante experimentos.

Algunos ejemplos importantes son:

La constante de estructura fina (α): Es un número que describe la fuerza de la interacción electromagnética, que es la fuerza que mantiene unidos a los átomos. Su valor es aproximadamente 1/137.036.
La relación de masa protón-electrón (β o μ): Es la relación entre la masa en reposo de un protón y la de un electrón. Su valor es aproximadamente 1836.

Estas constantes son como los "ingredientes básicos" del universo, y su valor no cambia.

Lista de magnitudes adimensionales comunes

Las magnitudes adimensionales son muy usadas en muchas áreas de la ciencia y la ingeniería. Aquí te mostramos algunas de las más comunes, especialmente en el estudio de los fluidos:

Magnitudes adimensionales
Nombre	Símbolo estándar	Fórmula	Definición	Campo de aplicación
Albedo	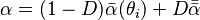$\alpha$	${\alpha}= (1-D) \bar \alpha(\theta_i) + D \bar{ \bar \alpha}$	Mide cuánta luz o radiación refleja una superficie o un cuerpo.	Climatología, astronomía
Ángulo	rad	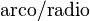$\rm arco/radio$	Medición de ángulos.	Matemáticas, trigonometría y geometría
Coeficiente de actividad	γ	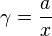$\gamma= \frac {{a}}{{x}}$	Muestra la "actividad" de una sustancia en una mezcla, comparada con su concentración.	Química
Coeficiente de arrastre (o coeficiente de Drag)	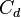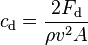$C_d$	$c_\mathrm d = \dfrac{2 F_\mathrm d}{\rho v^2 A}\,$	Cuantifica la resistencia que un objeto encuentra al moverse a través de un fluido (como el aire o el agua).	Mecánica de fluidos y Aerodinámica
Coeficiente de presión	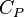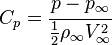$C_P$	$C_p = \cfrac{p-p_\infty}{\frac{1}{2} \rho_\infty V_\infty^2}$	Describe la presión relativa en un flujo de fluido.	Aerodinámica e hidrodinámica.
Coeficiente de sustentación	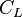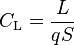$C_L$	$C_\mathrm L = \frac{L}{q S}$	Relaciona la fuerza de sustentación (la que levanta un avión) con la densidad del fluido, su velocidad y el área del objeto.	Aerodinámica
Factor Q (o factor de calidad)	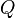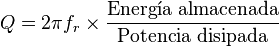$Q$	$Q = 2 \pi f_r \times \frac{\text{Energía almacenada}}{\text{Potencia disipada}} \,$	Mide la eficiencia de un sistema que oscila, como un circuito electrónico.	Electrónica
Factor de potencia	f.d.p.	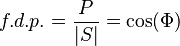$f.d.p. = \frac{P}{\|S\|} = \cos(\Phi) \!$	En un circuito de corriente alterna, indica qué tan bien se usa la energía eléctrica.	Electrotecnia
Índice de refracción	n	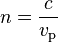$n = \frac{c}{v_{\mathrm {p}}}$	Determina cuánto se reduce la velocidad de la luz al pasar por un material.	Electromagnetismo, óptica
Número de Abbe	V	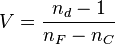$V = \frac{ n_d - 1 }{ n_F - n_C }$	Mide cómo se dispersa la luz en materiales ópticos.	Óptica
Número de Arquímedes	Ar	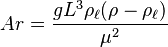$Ar = \frac{g L^3 \rho_\ell (\rho - \rho_\ell)}{\mu^2}$	Se usa para estudiar el movimiento de fluidos debido a diferencias de densidad.	Mecánica de fluidos
Número de Biot	Bi	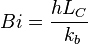$Bi = \frac{h L_C}{\ k_b}$	Relaciona la conductividad térmica en la superficie y en el interior de un sólido.	Transferencia de calor
Número de Bond	Bo	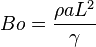$Bo = \frac{\rho a L^2}{\gamma}$	Relaciona las fuerzas de flotación con las fuerzas de tensión superficial.	Capilaridad
Número de capilaridad	Ca	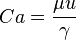$Ca=\frac{\mu u}{\gamma}$	Describe el flujo de un fluido cuando la tensión superficial es importante.	Dinámica de fluidos
Número de Damköhler	Da	$Da = k \tau$	Compara la velocidad de una reacción química con la velocidad de otros procesos en el sistema.	Química
Número de Deborah	De	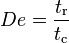$De = \frac{t_\mathrm{r}}{t_\mathrm{c}}$	Describe cuán "fluido" es un material, especialmente los viscoelásticos.	Reología, Mecánica de fluidos
Número de Eckert	Ec	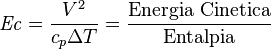$\mathit{Ec} = \frac{V^2}{c_p\Delta T} = \frac{\mbox{Energia Cinetica}}{\mbox{Entalpia}}$	Relaciona la energía cinética de un fluido con su entalpía en la transferencia de calor.	Mecánica de fluidos
Número de Ekman	Ek	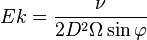$Ek=\frac{\nu}{2D^2\Omega\sin\varphi}$	En geofísica, compara las fuerzas viscosas con las fuerzas de Coriolis (debido a la rotación de un planeta).	Geofísica
Número de Eötvös	Eo	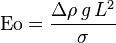$\mathrm{Eo}=\frac{\Delta\rho \,g \,L^2}{\sigma}$	Caracteriza la forma de burbujas o gotas, comparando las fuerzas de flotación con las de tensión superficial.	Dinámica de fluidos
Número de Euler	e	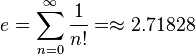$e = \displaystyle\sum\limits_{n = 0}^{ \infty} \dfrac{1}{n!} = \approx 2.71828$	Es la base de los logaritmos naturales.	Matemáticas
Número de Euler (física)	Eu	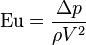$\mathrm{Eu}=\frac{\Delta{}p}{\rho V^2}$	Relaciona una pérdida de presión con la energía cinética del flujo.	Hidrodinámica
Número-f (o relación focal)	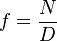$f$	$f=\frac{N}{D}$	Expresa la apertura de una lente en relación con su distancia focal, importante en fotografía.	Óptica, fotografía
Número de Froude	Fr	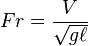$Fr = \frac{V}{\sqrt{g\ell}}$	Relaciona las fuerzas de inercia y las fuerzas de gravedad en un fluido.	Hidráulica
Número de Galilei	Ga	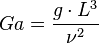$Ga = \frac{g \cdot L^3}{\nu^2}$	Compara las fuerzas gravitatorias con las fuerzas viscosas.	Mecánica de fluidos
Número de Grashof	Gr	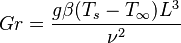$Gr = \frac{g \beta (T_s - T_\infty ) L^3}{\nu^2}$	Relaciona las fuerzas de flotación y las viscosas en la convección libre.	Mecánica de fluidos
Número Mach	M	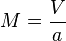$\ M = \frac {{V}}{{a}}$	Es la relación entre la velocidad de un objeto y la velocidad del sonido en el medio.	Aerodinámica
Número de Morton	Mo	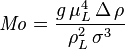$\mathit{Mo} = \frac{g \, \mu_L^4 \, \Delta \, \rho}{\rho_L^2 \, \sigma^3}$	Caracteriza la forma de burbujas y gotas.	Mecánica de fluidos e Hidráulica
Número de Nusselt	Nu	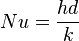$Nu =\frac{hd}{k}$	Mide el aumento de la transmisión de calor por convección comparado con la conducción.	Mecánica de fluidos
Número de Ohnesorge	Oh	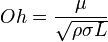$Oh = \frac{\mu}{\sqrt{\rho \sigma L }}$	Relaciona las fuerzas viscosas y las fuerzas de tensión superficial.	Mecánica de fluidos
Número de Péclet	Pe	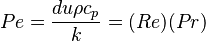$Pe = \frac{du\rho c_p}{k} = (Re)(Pr)$	Relaciona la velocidad de un flujo con la velocidad de difusión (de calor o masa).	Mecánica de fluidos
Número π	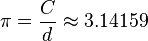$\pi$	$\pi = \frac{C}{d} \approx 3.14159$	Relación de la circunferencia de un círculo y su diámetro.	Matemáticas
Número de potencia (o número de Newton)	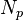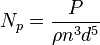$N_p$	$N_p = {P\over \rho n^3 d^5}$	Relaciona la fuerza de resistencia con la fuerza de inercia, usado en el consumo de energía por agitadores.	Electrotecnia
Número de Prandtl	Pr	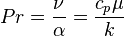$Pr = \frac{\nu}{\alpha} = \frac{c_p \mu}{k}$	Relación entre la viscosidad y la difusividad térmica.	Mecánica de fluidos
Número de Rayleigh	Ra	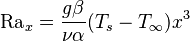$\mathrm{Ra}_{x} = \frac{g \beta} {\nu \alpha} (T_s - T_\infin) x^3$	Relaciona las fuerzas de flotación y las viscosas en la convección libre.	Mecánica de fluidos
Número de Reynolds	Re	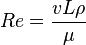$Re = \frac{vL\rho}{\mu}$	Muy importante en dinámica de fluidos, relaciona la densidad, viscosidad, velocidad y tamaño de un flujo.	Dinámica de fluidos
Número de Richardson	Ri	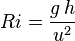$Ri = \frac{g \, h}{u^2}$	Relación entre la energía potencial y la energía cinética de un fluido.	Mecánica de fluidos
Número de Rossby (o número de Kibel)	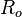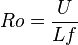$R_o$	$Ro=\frac{U}{Lf}$	Compara la aceleración de un fluido con la fuerza de Coriolis (debido a la rotación planetaria).	Geofísica y Mecánica de fluidos
Número de Schmidt	Sc	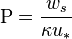$\mathrm{P} = \frac{w_s}{\kappa u_*}$	Compara la difusión de cantidad de movimiento con la difusión de masa.	Dinámica de fluidos
Número de Sherwood	Sh	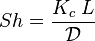$Sh = \frac{K_c \; L}{\mathcal{D}}$	Relaciona la transferencia de masa por convección y difusión.	Termodinámica y Mecánica de fluidos
Número de Stanton	St	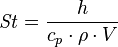$\mathit{St} = \frac{h}{c_p\cdot\rho\cdot V}$	Relaciona el calor transferido a un fluido con su capacidad calorífica.	Mecánica de fluidos
Número de Stokes	Stk o 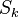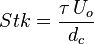$S_k$	$Stk = \frac{\tau\,U_o}{d_c}$	Describe el comportamiento de partículas suspendidas en un flujo.	Mecánica de fluidos
Número de Strouhal	St o Sr	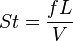$St = {f L\over V}$	Relaciona la oscilación de un flujo con su velocidad media.	Mecánica de fluidos
Número de Taylor	Ta	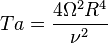$Ta = \frac{4\Omega^2 R^4}{\nu^2}$	Compara las fuerzas centrífugas con las fuerzas viscosas en un fluido que gira.	Mecánica de fluidos
Número de Weber	We	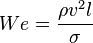$We = \frac{\rho v^2 l}{\sigma}$	Para fluidos con varias fases (como gotas en el aire), compara las fuerzas aerodinámicas con las fuerzas de tensión superficial.	Mecánica de fluidos
Número de Weissenberg	Wi	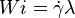$Wi = \dot{\gamma} \lambda$	En el estudio de flujos viscoelásticos, compara el tiempo de relajación del fluido con el tiempo del proceso.	Mecánica de fluidos
Número áureo	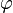$\varphi$	φ = (1+√5)/2	Una relación o proporción especial entre dos segmentos de una recta.	Matemáticas y estética

Véase también

En inglés: Dimensionless quantity Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Magnitud_adimensional&oldid=4895369»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Magnitud adimensional para Niños. Enciclopedia Kiddle.