Análisis dimensional para niños
El análisis dimensional es una herramienta muy útil que nos ayuda a entender y simplificar el estudio de fenómenos donde intervienen muchas medidas diferentes, como la longitud, el tiempo o la masa. Imagina que quieres saber cómo se mueve un coche o cómo vuela un avión; hay muchas cosas que influyen. El análisis dimensional nos permite reducir la cantidad de información que necesitamos para entenderlo.
Una de sus ideas principales es que podemos cambiar un grupo grande de medidas por un grupo más pequeño de "números adimensionales". Estos números especiales no tienen unidades (como metros o segundos), lo que hace que sean más fáciles de manejar. Aunque estos números no son únicos, siempre hay una cantidad mínima necesaria para estudiar un sistema.
Al usar el análisis dimensional, logramos:
- Entender mejor el sistema que estamos estudiando.
- Reducir mucho la cantidad de pruebas que necesitamos hacer para saber cómo funciona algo.
El análisis dimensional es la base de cómo se usan las maquetas a escala reducida en muchas áreas de la ingeniería, como la construcción de aviones, coches o edificios. Gracias a él, podemos probar un modelo pequeño y saber qué pasará con el objeto real, siempre y cuando haya una "semejanza física" entre ambos. Esto es posible porque los resultados de la maqueta son válidos para el modelo real si los números adimensionales son los mismos en ambos. Para esto, se usan "ecuaciones dimensionales", que son expresiones matemáticas que usan las unidades básicas (como el metro o el segundo) para comprobar fórmulas o dar unidades a un resultado.
Además, el análisis dimensional es una herramienta excelente para encontrar errores en los cálculos científicos y de ingeniería. Simplemente revisando que las unidades de los cálculos sean correctas, podemos detectar si algo anda mal.
¿Cómo funciona el Principio de Homogeneidad Dimensional?
El principio de homogeneidad dimensional es una regla fundamental que nos dice cómo deben estar formadas las ecuaciones que relacionan diferentes medidas físicas. Es como una regla de oro para que las ecuaciones tengan sentido. Este principio dice que solo podemos sumar o restar medidas físicas que sean del mismo tipo. Por ejemplo, no podemos sumar una longitud con un tiempo, o una masa con una longitud. ¡Sería como intentar sumar manzanas con peras!
Un ejemplo sencillo
Podemos entender este principio con el ejemplo de la energía de un objeto, que es la suma de su energía de movimiento (energía cinética) y su energía de posición (energía potencial).
Si escribimos las fórmulas de la energía cinética y potencial, tenemos:
Donde:
- E es la energía total.
- E_c es la energía cinética (por el movimiento).
- E_p es la energía potencial (por la posición).
- m es la masa del objeto.
- v es su velocidad.
- g es la aceleración de la gravedad.
- h es la altura.
Si expresamos la velocidad y la aceleración usando las medidas fundamentales (longitud 'L', masa 'M', tiempo 'T'), la ecuación se ve así:
Y si lo vemos en términos de sus dimensiones (sin los números):
Como puedes ver, tanto la energía cinética (un medio de la masa por la velocidad al cuadrado) como la energía potencial (la masa por la gravedad y por la altura) tienen las mismas dimensiones. Ambas son formas de energía.
Este principio de homogeneidad dimensional asegura que una ecuación física sea coherente. Es importante recordar que los números puros (como 2, 3.1416, etc.) no tienen dimensiones, pero las constantes físicas (como la velocidad de la luz) sí tienen dimensiones. Por ejemplo:
- e = 2,718281... (la base de los logaritmos naturales) →
![[e] = 1](/images/math/1/c/6/1c670a1ea6d7fb64d887568b72a1a99c.png) (no tiene dimensiones);
(no tiene dimensiones); - c = 299 792 458 m/s (la velocidad de la luz en el vacío) →
![[c] = [v] = LT^{-1}](/images/math/6/e/a/6ea89813a590867b9ee9a91e9c73ec9b.png) (tiene dimensiones de longitud dividida por tiempo).
(tiene dimensiones de longitud dividida por tiempo).
Véase también
 En inglés: Dimensional analysis Facts for Kids
En inglés: Dimensional analysis Facts for Kids


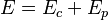
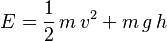
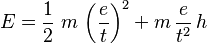
![E =
\frac{1}{2} \, [M] [L]^2 [T]^{-2} +
[M] [L]^2 [T]^{-2}](/images/math/f/1/5/f155895d77a13a33a844023d2db03722.png)