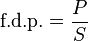Factor de potencia para niños
El factor de potencia (f.d.p.) es un número que nos dice qué tan bien se usa la energía eléctrica en un circuito de corriente alterna. Imagina que la energía eléctrica es como una bebida: una parte es la que realmente usas (la bebida en sí, la "potencia activa"), y otra parte es como la espuma que no puedes beber (la "potencia reactiva"). El factor de potencia nos dice qué porcentaje de la bebida es realmente útil.
Se calcula dividiendo la potencia activa (la energía útil) entre la potencia aparente (la energía total que se entrega). Un factor de potencia cercano a 1 (o 100%) significa que casi toda la energía se está usando de forma útil, ¡lo cual es muy bueno! Si el factor de potencia es bajo, significa que se está desperdiciando mucha energía.
Contenido
¿Cómo se calcula el Factor de Potencia?
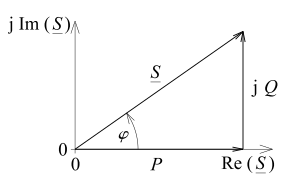
El factor de potencia se define como la división de la potencia activa (P) entre la potencia aparente (S):
Es importante saber que el factor de potencia (f.d.p.) y el coseno del ángulo phi (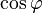
) no siempre son lo mismo. En algunos tipos de circuitos, llamados "lineales", sí coinciden. Pero en otros, llamados "no lineales", son diferentes.
Podemos decir que:
- Si el factor de potencia está "adelantado", significa que la corriente eléctrica va un poco antes que el voltaje. Esto suele pasar con aparatos que tienen componentes capacitivos.
- Si el factor de potencia está "atrasado", la corriente eléctrica va un poco después que el voltaje. Esto es común en aparatos con componentes inductivos.
Para medir el factor de potencia se usa un aparato especial llamado cosímetro.
Tipos de circuitos: Lineales y No Lineales
La forma en que se calcula el factor de potencia puede variar un poco dependiendo del tipo de circuito eléctrico.
Circuitos Lineales
En los circuitos lineales, la corriente y el voltaje tienen una forma de onda muy suave y regular, como una ola perfecta. En estos casos, el factor de potencia es igual al coseno del ángulo que se forma entre la corriente y el voltaje.
Por ejemplo, una bombilla antigua (incandescente) es un buen ejemplo de carga lineal. Para una resistencia ideal, el factor de potencia es 1, lo que significa que toda la energía se convierte en luz y calor útil. Para componentes como bobinas o condensadores ideales, el factor de potencia es 0, porque no usan energía de forma útil, solo la almacenan y la devuelven.
Circuitos No Lineales
En los circuitos no lineales, la forma de la onda de la corriente no es tan perfecta. Esto ocurre porque algunos aparatos modernos, como los cargadores de teléfonos o las computadoras, usan la electricidad de una manera que crea "armónicos". Los armónicos son como pequeñas ondas extra que se suman a la onda principal y pueden causar que la energía se use de forma menos eficiente.
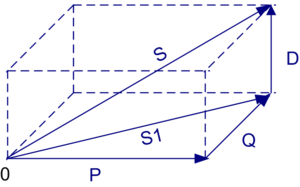
En estos casos, el cálculo del factor de potencia es un poco más complejo porque hay una parte de la potencia que se pierde debido a esta "distorsión".
¿Por qué es importante un buen Factor de Potencia?
Tener un buen factor de potencia (cercano a 1) es muy importante por varias razones:
- Ahorro de energía: Un factor de potencia bajo significa que se necesita más corriente para hacer el mismo trabajo. Esto es como tener que empujar más fuerte para mover algo, pero solo una parte de tu fuerza es realmente útil.
- Cables más pequeños: Si la corriente es muy alta debido a un factor de potencia bajo, se necesitan cables más gruesos para transportarla. Los cables más gruesos son más caros.
- Equipos más pequeños: Los generadores y transformadores que producen y distribuyen la electricidad también tienen que ser más grandes si el factor de potencia es bajo. Esto aumenta los costos de la instalación eléctrica.
- Menos pérdidas: Cuando la corriente viaja por los cables, siempre hay una pequeña pérdida de energía en forma de calor. Si la corriente es más alta (por un factor de potencia bajo), estas pérdidas son mayores.
- Mejor voltaje: Un buen factor de potencia ayuda a mantener el voltaje estable en la red eléctrica, lo que es bueno para todos los aparatos conectados.
Las compañías eléctricas suelen cobrar multas a las empresas o grandes consumidores que tienen un factor de potencia muy bajo, porque les cuesta más entregar la energía.
¿Qué tipos de aparatos afectan el Factor de Potencia?
El valor del factor de potencia depende de los aparatos que estén conectados en una instalación.
- Aparatos resistivos: Son los que convierten casi toda la energía eléctrica en calor o luz, como las bombillas incandescentes (las antiguas) o las estufas eléctricas. Estos aparatos tienen un factor de potencia cercano a 1.
- Aparatos inductivos: Son los que usan bobinas o motores, como los transformadores, los motores de lavadoras o refrigeradores, y algunas lámparas fluorescentes. Estos aparatos hacen que la corriente se "atrase" respecto al voltaje y suelen tener un factor de potencia bajo.
- Aparatos capacitivos: Son menos comunes en los hogares, pero incluyen algunos tipos de condensadores. Estos aparatos hacen que la corriente se "adelante" respecto al voltaje.
En general, los aparatos con motores o componentes electrónicos complejos (como computadoras, televisores, cargadores) suelen tener un factor de potencia más bajo que los aparatos puramente resistivos.
¿Cómo se mejora el Factor de Potencia?
Es posible mejorar el factor de potencia de un sistema eléctrico para que esté más cerca de 1. Esto se llama "corrección del factor de potencia".
La forma más común de hacerlo es conectando unos componentes llamados condensadores (también conocidos como capacitores) en el circuito. Los condensadores tienen el efecto contrario a los motores y bobinas: si los motores hacen que la corriente se atrase, los condensadores hacen que se adelante. Al combinarlos de forma adecuada, se puede equilibrar el circuito y hacer que el factor de potencia mejore.
Las empresas eléctricas exigen a los grandes consumidores que mantengan su factor de potencia dentro de ciertos límites para que la red funcione de manera eficiente. Si no lo hacen, pueden tener que pagar más. Por eso, muchas industrias instalan sistemas automáticos que conectan o desconectan condensadores según sea necesario para mantener un buen factor de potencia.
Galería de imágenes
-
Esquema de un triángulo de potencias mostrando la modificación del factor de potencia mediante la adición de capacitores.
Véase también
En inglés: Power factor Facts for Kids
