Carl Friedrich Gauss para niños
Datos para niños Carl Friedrich Gauss |
||
|---|---|---|
 Retrato hecho por Christian Albrecht Jensen.
|
||
| Información personal | ||
| Nombre de nacimiento | Johann Carl Friedrich Gauß | |
| Nacimiento | 30 de abril de 1777 Brunswick, Principado de Brunswick-Wolfenbüttel |
|
| Fallecimiento | 23 de febrero de 1855 Gotinga, Reino de Hanóver |
|
| Causa de muerte | Arteriosclerosis e insuficiencia cardíaca | |
| Sepultura | Albanifriedhof | |
| Residencia | Reino de Hanóver | |
| Lengua materna | bajo alemán | |
| Familia | ||
| Padres | Gebhard Dietrich Gauss Dorthea Benze |
|
| Cónyuge | Johanna Osthoff Mina Waldeck |
|
| Educación | ||
| Educación | doctor en Filosofía | |
| Educado en | Universidad de Gotinga, Universidad de Helmstedt | |
| Supervisor doctoral | Johann Friedrich Pfaff | |
| Información profesional | ||
| Área | Matemático y físico | |
| Conocido por |
Teoría de números Heptadecágono, Eliminación de Gauss-Jordan |
|
| Empleador | Universidad de Gotinga | |
| Estudiantes doctorales | Christoph Gudermann Christian Ludwig Gerling J. W. Richard Dedekind Johann Encke Johann Listing Bernhard Riemann |
|
| Obras notables |
|
|
| Miembro de |
|
|
| Distinciones |
|
|
| Firma | ||
 |
||
Johann Carl Friedrich Gauss (nacido en Brunswick, el 30 de abril de 1777 y fallecido en Gotinga, el 23 de febrero de 1855) fue un matemático, astrónomo, geodesta y físico alemán. Hizo contribuciones muy importantes en muchas áreas de la ciencia.
Gauss fue conocido como el "Príncipe de los Matemáticos" por su gran influencia en las matemáticas y la ciencia. Fue uno de los primeros en aplicar el concepto de divisibilidad a otros grupos de números, no solo a los números enteros.
Desde muy joven, Gauss fue reconocido como un niño prodigio. A pesar de que sus padres no tenían mucha educación, él mostró un talento increíble. Hizo sus primeros grandes descubrimientos cuando era adolescente. A los 21 años, completó su obra más importante, Disquisitiones arithmeticae, que se publicó en 1801. Este libro es fundamental para la teoría de números y sigue siendo muy importante hoy en día.
Contenido
Biografía de Carl Friedrich Gauss
Infancia y juventud de un genio
Johann Carl Friedrich Gauss nació en el Ducado de Brunswick, Alemania, en una familia humilde. Su madre, Dorothea Gauss, era inteligente y alegre. Su padre, Gebhard Dietrich Gauss, tuvo varios trabajos. Se cuenta que Carl Friedrich, con solo tres años, ya corregía las cuentas de su padre.
Desde muy pequeño, aprendió aritmética elemental sin ayuda. Él mismo dijo que aprendió a calcular antes que a hablar. En 1784, a los siete años, entró a la escuela. Su maestro, Büttner, notó su talento y lo animó a seguir estudiando.
Una famosa anécdota cuenta que, a los nueve años, su maestro les pidió sumar los números del 1 al 100. Gauss encontró la respuesta muy rápido. En lugar de sumar uno por uno, se dio cuenta de que podía agrupar los números: 1+100=101, 2+99=101, y así sucesivamente. Había 50 de estas parejas, así que la suma era 101 x 50 = 5050. Así, descubrió una fórmula para sumar series de números.
A los catorce años, el duque de Brunswick decidió apoyarlo económicamente. Esto le permitió estudiar en el Collegium Carolinum, una escuela de élite. Allí, Gauss aprendió griego y latín muy rápido. Al terminar, no sabía si dedicarse a las matemáticas o a las lenguas. En esa época, ya había descubierto su método de los mínimos cuadrados, mostrando su interés temprano en cómo manejar errores en las observaciones.
A los diecisiete años, tuvo ideas sobre un nuevo tipo de geometría. A los dieciocho, se dedicó a la aritmética, que se convirtió en su gran pasión. Para él, "las matemáticas serían la reina de las ciencias y la teoría de números sería la reina de las matemáticas".
Logros y madurez científica
En 1796, Gauss demostró cómo dibujar un polígono regular de 17 lados usando solo regla y compás. Este fue un gran avance.
También fue el primero en probar de forma rigurosa el teorema fundamental del álgebra en 1799. Este teorema dice que toda ecuación con polinomios tiene al menos una solución.
En 1801, publicó su libro Disquisitiones arithmeticae. Este libro organizó y mejoró la teoría de números. Ese mismo año, predijo la órbita de Ceres, un planetoide recién descubierto, usando su método de los mínimos cuadrados. Su predicción fue muy precisa y ayudó a encontrar a Ceres de nuevo.
En 1809, Gauss fue nombrado director del Observatorio de Gotinga, donde trabajó el resto de su vida. Publicó Theoria motus corporum coelestium in sectionibus conicis Solem ambientium, un libro sobre cómo calcular las órbitas de los planetas. Sus métodos, aunque adaptados a las computadoras modernas, siguen siendo muy importantes.
Gauss también trabajó en otras áreas. Dirigió el estudio topográfico de Hannover, un trabajo de medición de tierras. Con el físico Wilhelm Weber, investigó la electricidad y el magnetismo. Juntos, crearon el primer telégrafo electromecánico en 1833.
En 1835, Carl Friedrich Gauss formuló la ley de Gauss. Esta ley es muy importante en el electromagnetismo y es una de las bases de las ecuaciones de Maxwell. Gauss era muy cuidadoso con su trabajo y solo publicaba lo que consideraba perfecto, siguiendo su lema "Pauca sed matura" (Poco, pero maduro). Su rigor ha influido en las matemáticas hasta hoy.
Vida familiar
Gauss se casó con Johanna Elizabeth Rosina Osthoff en 1805. Tuvieron tres hijos. Johanna falleció en 1809, lo que causó una gran tristeza a Gauss. Se volvió a casar con Friederica Wilhelmine Waldeck, la mejor amiga de Johanna. Tuvieron tres hijos más. Friederica falleció en 1831. Su hija Henriette se encargó del hogar hasta la muerte de Gauss en Gotinga el 23 de febrero de 1855.
Obras importantes de Gauss
Disquisitiones arithmeticae

Gauss pasó tres años muy productivos en Gotinga. A finales de 1798, regresó a Brunswick con su obra maestra, Disquisitiones arithmeticae, casi lista. Se publicó en 1801.
Este libro, escrito en latín, está dedicado a su protector, el duque Ferdinand. Es un tratado sobre la teoría de números que resume y mejora todo el trabajo anterior en esta área. El libro tiene seis secciones dedicadas a la teoría de números.
Contribuciones a la teoría del potencial
El teorema de la divergencia de Gauss, de 1835, es fundamental en la teoría del potencial y la física. Este teorema relaciona cómo se comporta un campo vectorial dentro de un volumen con lo que sucede en la superficie que lo rodea.
Descubrimientos y aportes de Gauss
En el campo del álgebra
En su tesis doctoral de 1799, Gauss demostró el teorema fundamental del álgebra. Este teorema dice que cualquier polinomio (una expresión matemática con variables y números) que no sea constante y tenga números complejos, tiene al menos una solución compleja. Gauss hizo otras tres pruebas de este teorema, y sus trabajos ayudaron a entender mejor los números complejos.
Gauss también hizo grandes aportes a la teoría de los números con su libro de 1801, Disquisitiones Arithmeticae. En este libro, introdujo el símbolo de la "triple barra" (≡) para la congruencia y lo usó en la aritmética modular. También demostró que un heptadecágono regular (un polígono de 17 lados) se puede construir con regla y compás.
En la astronomía
El 1 de enero de 1801, el astrónomo italiano Giuseppe Piazzi descubrió el planeta enano Ceres. Piazzi solo pudo observarlo por un mes antes de que desapareciera detrás del Sol. Los matemáticos de la época no podían predecir su posición con tan pocos datos. Gauss se enteró del problema y, después de tres meses de trabajo, predijo dónde estaría Ceres en diciembre de 1801. Su predicción fue muy precisa, y Ceres fue redescubierto. Esto llevó a que Ceres fuera clasificado como el primer asteroide (ahora planeta enano) descubierto.
En el levantamiento de tierras
En 1818, Gauss usó sus conocimientos para hacer un levantamiento topográfico del Reino de Hannover. Para este trabajo, inventó el heliotropo, un instrumento que usa un espejo para reflejar la luz del sol a grandes distancias y así medir posiciones con precisión.
En las geometrías no euclidianas
Gauss también descubrió la posibilidad de geometrías no euclidianas, pero nunca publicó sus hallazgos. Este descubrimiento fue un cambio muy importante en las matemáticas, ya que mostró que los axiomas de Euclides no eran la única forma de tener una geometría lógica.
En el magnetismo
En 1831, Gauss comenzó a trabajar con el profesor de física Wilhelm Weber. Esta colaboración llevó a nuevos descubrimientos sobre el magnetismo y la electricidad. Juntos, construyeron el primer telégrafo electromecánico en 1833, que conectaba el observatorio con el instituto de física en Gotinga. Gauss también ordenó la construcción de un observatorio magnético y fundó una asociación para estudiar el campo magnético de la Tierra. Desarrolló un método para medir la intensidad del campo magnético que se usó por mucho tiempo.
Publicaciones importantes
- 1799: Su tesis doctoral sobre el teorema fundamental del álgebra.
- 1801: Disquisitiones Arithmeticae.
- 1809: Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium (Teoría del movimiento de los cuerpos celestes que giran alrededor del sol en secciones cónicas).
- 1821, 1823 y 1826: Theoria combinationis observationum erroribus minimis obnoxiae (Teoría de la combinación de observaciones con errores mínimos).
- 1827: Disquisitiones generales circa superficies curvas (Investigaciones generales sobre superficies curvas).
Cosas nombradas en honor a Gauss
Muchas cosas llevan el nombre de Carl Friedrich Gauss para honrar sus contribuciones:
- El Premio Carl Friedrich Gauss, un premio de matemáticas.
- El gauss, una unidad de medida de campo magnético.
- La Expedición Gauss, una expedición alemana a la Antártida.
- El cañón Gauss, un tipo de cañón que usa electroimanes.
- Gauss, un personaje en el videojuego Warframe.
- GAUSS, un lenguaje de programación.
- La Torre Gauss o Gaußturm, una torre de observación en Alemania.
- El asteroide (1001) Gaussia.
- El cráter lunar Gauss.
- Fórmulas y teoremas matemáticos y físicos:
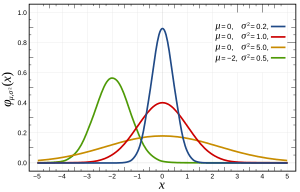
- La distribución normal o distribución de Gauss, muy usada en estadística.
- La curva de Gauss o función gaussiana.
- La ley de Gauss, sobre el flujo eléctrico.
- El teorema de la divergencia, también llamado teorema de Gauss.
- El teorema de Gauss-Bonnet, que conecta la geometría y la topología de las superficies.
- El sistema Gauss-Krüger, usado en cartografía.
- La cuadratura de Gauss, un método para calcular integrales.
- La eliminación de Gauss-Jordan, un algoritmo para resolver sistemas de ecuaciones.
Galería de imágenes
-
Tumba de Gauss en el Cementerio Albani en Gotinga, Alemania.
Véase también
 En inglés: Carl Friedrich Gauss Facts for Kids
En inglés: Carl Friedrich Gauss Facts for Kids





