Número de Bernoulli para niños
Los números de Bernoulli son una secuencia especial de números que aparecen en muchas áreas de las matemáticas. Se les llama así en honor a Jacob Bernoulli, un matemático que los estudió por primera vez.
Estos números son muy útiles para resolver problemas de sumas, como calcular rápidamente la suma de los primeros números naturales (1 + 2 + 3 + ... + n) o la suma de sus cuadrados (1² + 2² + 3² + ... + n²), o incluso potencias más altas.
Contenido
¿Para qué sirven los números de Bernoulli?
Una de las principales razones por las que los números de Bernoulli son importantes es que nos ayudan a encontrar fórmulas para sumar potencias de números naturales. Imagina que quieres sumar:
- 1 + 2 + 3 + ... + n
- 1² + 2² + 3² + ... + n²
- 1³ + 2³ + 3³ + ... + n³
Para cada una de estas sumas, existe una fórmula que te permite encontrar el resultado sin tener que sumar todos los números uno por uno. Por ejemplo, para la suma de los primeros números naturales (1 + 2 + ... + n), la fórmula es: 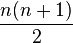
Los números de Bernoulli son clave para encontrar estas fórmulas para potencias más altas. Las fórmulas resultantes siempre son polinomios, que son expresiones matemáticas con sumas y restas de términos con diferentes potencias de una variable.
Por ejemplo, si queremos sumar los primeros números naturales (1 + 2 + ... + n), usando los números de Bernoulli, la fórmula se ve así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sum_{m=1}^{n} m = \frac{n^2 + n} {2}
¿Quién descubrió y trabajó con ellos?
Los números de Bernoulli fueron nombrados por Abraham de Moivre en honor a Jacob Bernoulli, quien fue el primero en investigarlos a fondo.
Un dato interesante es que el primer método para calcular estos números de forma automática fue descrito por Ada Lovelace en 1843. Ella lo hizo en sus notas sobre la máquina analítica de Charles Babbage, que fue una de las primeras ideas para una computadora.
¿Cómo se definen los números de Bernoulli?
Los números de Bernoulli son una secuencia de números racionales (es decir, números que se pueden escribir como una fracción). Se pueden definir de varias maneras, pero una forma común es a través de una "función generadora". Piensa en una función generadora como una máquina que, al expandirse en una serie, produce los números de Bernoulli como sus coeficientes.
Algunos valores de los números de Bernoulli
Aquí tienes los primeros números de Bernoulli. Verás que algunos son fracciones y otros son cero.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bn | 1 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \pm \frac{1}{2} | 16 | 0 | −130 | 0 | 142 | 0 | −130 | 0 | 566 | 0 | −6912730 |
Como puedes ver, todos los números de Bernoulli con un índice impar (excepto el B₁), como B₃, B₅, B₇, etc., son cero. Esto es una propiedad muy interesante de estos números.
Galería de imágenes
Véase también
 En inglés: Bernoulli number Facts for Kids
En inglés: Bernoulli number Facts for Kids