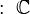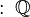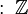Número entero para niños
Un número entero es un tipo de número que incluye a los números naturales (como 0, 1, 2, 3, y así sucesivamente), sus opuestos (como -1, -2, -3, etc.), y el cero. Los números enteros negativos, como −1 o −13, son más pequeños que cero y también más pequeños que todos los números positivos. Para mostrar si un número es negativo, se le pone un signo «menos» delante: -1, -5. Si un número no tiene signo, se entiende que es positivo.
El conjunto de todos los números enteros se representa con la letra 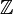 . Esta letra viene de la palabra en alemán Zahlen, que significa «números».
. Esta letra viene de la palabra en alemán Zahlen, que significa «números».
En la recta numérica, los números negativos se colocan a la izquierda del cero, y los números positivos se colocan a su derecha.
Los números enteros se pueden sumar, restar, multiplicar y dividir. Para estas operaciones, se siguen las mismas reglas que con los números naturales, pero se añaden normas especiales para usar los signos.
Los números enteros son muy útiles porque nos permiten contar cosas que van más allá de lo que podemos ver o tener. Por ejemplo, si en un colegio entran 80 alumnos nuevos, pero 100 alumnos de último curso se van, en total habrá 100 − 80 = 20 alumnos menos. También podemos decir que el número de alumnos cambió en 80 − 100 = −20.
Algunas medidas, como la temperatura o la altura, usan valores por debajo del cero. La altura del Everest es de 8848 metros sobre el nivel del mar. En cambio, la orilla del mar Muerto está 423 metros por debajo del nivel del mar, lo que se puede expresar como −423 m.
Contenido
Un poco de historia de los números enteros
La palabra "entero" viene del latín integer, que significa "completo" o "intacto". Al principio, este término se usaba solo para los números positivos que eran múltiplos de 1, es decir, los mismos números naturales.
Con el tiempo, la definición de número entero se hizo más grande para incluir también a los números negativos. Esto ocurrió porque los matemáticos se dieron cuenta de lo útiles que eran. Por ejemplo, Leonhard Euler, un famoso matemático, ya en 1765 incluyó tanto los números positivos como los negativos en su definición de números enteros. Sin embargo, muchos matemáticos en Europa tardaron en aceptar los números negativos hasta mediados del siglo XIX.
El uso de la letra Z para representar el conjunto de los números enteros viene de la palabra alemana Zahlen ("números"). Se cree que fue el matemático David Hilbert quien empezó a usarla. Esta notación se hizo muy común en los libros de matemáticas a partir de 1947.
¿Qué son los números enteros?
Los números negativos son necesarios para hacer operaciones como:
- 3 − 5 = ?
Cuando el primer número (minuendo) es más pequeño que el segundo (sustraendo), la resta no se puede hacer solo con números naturales. Sin embargo, hay situaciones en las que los números negativos son muy útiles, como cuando hablamos de ganancias y pérdidas.
Ejemplo: Imagina que una persona juega a un juego. Si el primer día gana 2000 pesos y al día siguiente pierde 1000, en total ganó 2000 − 1000 = $1000. Pero si el primer día gana 500 y al siguiente pierde 2000, entonces perdió 2000 − 500 = $1500. Para no tener que decir "ganó en total" o "perdió en total", podemos usar los signos: en el primer caso ganó +$1000 y en el segundo ganó −$1500. Así, una pérdida se puede ver como una "ganancia negativa".
Números con signo: Positivos y Negativos
Los números naturales 0, 1, 2, 3... son los números que usamos normalmente para contar. Si les ponemos un signo menos («−») delante, se convierten en números negativos.
Un número entero negativo es un número natural como 1, 2, 3, etc., pero con un signo menos delante. Por ejemplo: −1, −2, −3. Se leen «menos 1», «menos 2», «menos 3», y así.
Para distinguirlos mejor, a los números naturales se les puede añadir un signo más («+») delante y se les llama números positivos.
Un número entero positivo es un número natural como 1, 2, 3,... con un signo más delante.
El cero no es positivo ni negativo. Se puede escribir con signo más, menos o sin signo, porque sumar o restar cero no cambia nada. Todos estos números juntos (positivos, negativos y el cero) forman el conjunto de los «números enteros».
Los números enteros son el conjunto de todos los números con signo (positivos y negativos) junto con el 0. Se representan con la letra 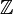 :
: 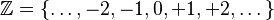
La recta numérica: Un mapa de los números
Los números enteros negativos son más pequeños que todos los positivos y que el cero. En la recta numérica, un número es mayor cuanto más a la derecha esté. Para entender cómo se ordenan, usamos la recta numérica:
En esta representación, vemos que los números negativos son más pequeños cuanto más a la izquierda están. Es decir, cuanto mayor es el número después del signo negativo, más pequeño es el número entero. A este número sin su signo se le llama el valor absoluto.
El valor absoluto: La distancia al cero
El valor absoluto de un número entero es la distancia que hay desde el cero hasta ese número en la recta numérica. El valor absoluto de 0 es 0. Se representa con dos barras verticales «||».
Ejemplos. |+5| = 5 , |−2| = 2 , |0| = 0.
El orden de los números enteros se puede resumir así:
- Si tienes un número positivo (+a) y uno negativo (−b), el negativo siempre es menor que el positivo: −b < +a.
- Si tienes dos números con el mismo signo:
* Si ambos son positivos, el menor es el que tiene el valor absoluto más pequeño. * Si ambos son negativos, el menor es el que tiene el valor absoluto más grande (porque está más a la izquierda en la recta).
- El cero (0) es menor que todos los números positivos y mayor que todos los números negativos.
Ejemplos. +23 > −56 , +31 < +47 , −15 < −9 , 0 > −36
Operaciones con números enteros: ¡A calcular!
Los números enteros se pueden sumar, restar, multiplicar y dividir, igual que los números naturales.
Suma de números enteros
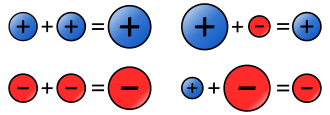
Para sumar dos números enteros, primero se decide el signo y luego se calcula el valor absoluto del resultado:
- Si los dos números tienen el mismo signo: El resultado tendrá ese mismo signo, y su valor absoluto será la suma de los valores absolutos de los números.
- Si los dos números tienen signos diferentes:
* El signo del resultado será el signo del número con el valor absoluto más grande. * El valor absoluto del resultado será la resta del valor absoluto más grande menos el valor absoluto más pequeño.
Ejemplos. (+21) + (−13) = +8 , (+17) + (+26) = +43 , (−41) + (+19) = −22 , (−33) + (−28) = −61
La suma de números enteros tiene propiedades importantes:
- Propiedad asociativa: Si sumas tres números enteros (a + b) + c es lo mismo que a + (b + c). El orden en que agrupas no cambia el resultado.
- Propiedad conmutativa: Si sumas dos números enteros a + b es lo mismo que b + a. El orden de los números no cambia el resultado.
- Elemento neutro: Si sumas 0 a cualquier número entero a, el número no cambia: a + 0 = a.
Ejemplo de propiedades:
- Propiedad asociativa:
- [ (−13) + (+25) ] + (+32) = (+12) + (+32) = (+44)
- (−13) + [ (+25) + (+32) ] = (−13) + (+57) = (+44)
- Propiedad conmutativa:
- (+9) + (−17) = −8
- (−17) + (+9) = −8
Además, la suma de números enteros tiene una propiedad extra:
- Elemento opuesto o simétrico: Para cada número entero a, existe otro entero −a (su opuesto), que al sumarlo al primero da cero: a + (−a) = 0.
Resta de números enteros
La resta de números enteros es muy sencilla, porque se convierte en una suma. Para restar dos números enteros (minuendo menos sustraendo), se suma el primer número (minuendo) con el opuesto del segundo número (sustraendo).
Ejemplos (+10) − (−5) = (+10) + (+5) = +15 (−7) − (+6) = (−7) + (−6) = −13 (−4) − (−8) = (−4) + (+8) = + 4 (+2) − (+9) = (+2) + (−9) = −7
Multiplicación y división de números enteros
Para la multiplicación y la división de dos números enteros, también se calcula el valor absoluto y el signo por separado:
- El valor absoluto es el resultado de multiplicar (o dividir) los valores absolutos de los números.
- El signo es «+» si los signos de los números son iguales, y «−» si son diferentes.
Para recordar el signo del resultado, se usa la regla de los signos:
Regla de los signos - Multiplicación
- (+) × (+) = (+) (Más por más es más)
- (+) × (−) = (−) (Más por menos es menos)
- (−) × (+) = (−) (Menos por más es menos)
- (−) × (−) = (+) (Menos por menos es más)
Regla de los signos - División
- (+) : (+) = (+) (Más entre más es más)
- (+) : (−) = (−) (Más entre menos es menos)
- (−) : (+) = (−) (Menos entre más es menos)
- (−) : (−) = (+) (Menos entre menos es más)
Ejemplos de multiplicación. (+5) × (+3) = +15 , (+4) × (-6) = -24 , (−7) × (+8) = −56 , (−9) × (−2) = +18.
Ejemplos de división. (+15) : (+3) = +5 , (+12) : (-6) = -2 , (−16) : (+4) = −4 , (−18) : (−2) = +9.
La multiplicación de números enteros también tiene propiedades importantes:
- Propiedad asociativa: Si multiplicas tres números enteros (a × b) × c es lo mismo que a × (b × c). El orden en que agrupas no cambia el resultado.
- Propiedad conmutativa: Si multiplicas dos números enteros a × b es lo mismo que b × a. El orden de los números no cambia el resultado.
- Elemento neutro: Si multiplicas cualquier número entero a por 1, el número no cambia: a × 1 = a.
Ejemplo de propiedades:
- Propiedad asociativa:
- [ (−7) × (+4) ] × (+5) = (−28) × (+5) = −140
- (−7) × [ (+4) × (+5) ] = (−7) × (+20) = −140
- Propiedad conmutativa:
- (−6) × (+9) = −54
- (+9) × (−6) = −54
La suma y la multiplicación de números enteros están relacionadas por la propiedad distributiva:
- Propiedad distributiva: Si tienes tres números enteros a, b y c, el producto a × (b + c) es igual a la suma de productos (a × b) + (a × c).
Ejemplo.
- (−7) × [ (−2) + (+5) ] = (−7) × (+3) = −21
- [ (−7) × (−2) ] + [ (−7) × (+5) ] = (+14) + (−35) = −21
Es importante saber que la división de números enteros no tiene las propiedades asociativa, conmutativa ni la distributiva.
Véase también
 En inglés: Integer Facts for Kids
En inglés: Integer Facts for Kids
- Parte entera
- Número decimal
|