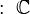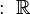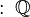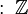Número decimal para niños

Un número decimal es un tipo de número que tiene una parte entera y una parte fraccionaria, separadas por una coma o un punto. Por ejemplo, en el número 3,14, el "3" es la parte entera y el "14" es la parte fraccionaria. Estos números se usan mucho en la vida diaria, como cuando hablamos de precios, medidas o calificaciones.

En matemáticas, a veces se usa el término "número decimal" de una forma más específica. Se refiere a los números que se pueden escribir como una fracción donde el denominador es una potencia de 10 (como 10, 100, 1000, etc.). Estos números tienen una cantidad finita (limitada) de cifras después de la coma. Por ejemplo, 0,5 (que es 5/10) o 2,332 (que es 2332/1000).

Sin embargo, en muchos lugares, cuando decimos "número decimal", nos referimos a cualquier número que tenga una parte entera y una parte fraccionaria, incluso si las cifras después de la coma son infinitas. Esto incluye números como π (3,14159...) o la raíz cuadrada de 2 (1,41421...).

¿Qué es un número decimal exacto?

Un número decimal exacto es aquel que tiene un número limitado de cifras después de la coma. Esto significa que la parte decimal "termina". Por ejemplo, 0,25 es un número decimal exacto porque solo tiene dos cifras después de la coma.

Estos números se pueden escribir como una fracción donde el número de abajo (el denominador) es una potencia de 10.

• Ejemplos:
  • 0,5 se puede escribir como 5/10.
  • 2,332 se puede escribir como 2332/1000.
  • Los números enteros también son decimales exactos. Por ejemplo, 3 se puede escribir como 3,0 o 3,00.

¿Cómo se dividen los números decimales?

Los números decimales se pueden clasificar según cómo son sus cifras después de la coma.

• Números decimales exactos: Tienen un número finito de cifras después de la coma.
• Números decimales infinitos: Tienen un número ilimitado de cifras después de la coma. Estos se dividen en:

* Periódicos: Sus cifras se repiten en un patrón. * No periódicos: Sus cifras no se repiten en ningún patrón.

Números decimales periódicos

Los números decimales periódicos son aquellos que tienen una o más cifras que se repiten sin fin después de la coma. A este grupo de cifras que se repiten se le llama periodo.

Decimal periódico puro

En estos números, el patrón que se repite (el periodo) empieza justo después de la coma.

• Ejemplo:
  • 0,3333... se escribe como 0,overline3. Aquí, el "3" se repite infinitamente. Este número es igual a la fracción 1/3.

Decimal periódico mixto

En estos números, hay algunas cifras después de la coma que no se repiten (el anteperiodo), y luego viene un patrón que sí se repite (el periodo).

• Ejemplo:
  • 0,16666... se escribe como 0,1overline6. Aquí, el "1" es el anteperiodo y el "6" es el periodo. Este número es igual a la fracción 1/6.

Los números decimales periódicos (puros y mixtos) siempre se pueden escribir como una fracción.

Números decimales no periódicos

Estos números tienen una cantidad infinita de cifras después de la coma, pero estas cifras no siguen ningún patrón que se repita. Son los números irracionales.

• Algunos ejemplos famosos son:
  • π (pi), que es aproximadamente 3,14159265...
  • La constante de Euler (e), que es aproximadamente 2,71828...
  • La raíz cuadrada de 2 (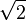), que es aproximadamente 1,41421356...

Como estos números tienen infinitas cifras que no se repiten, no se pueden escribir como una fracción simple. Para usarlos en cálculos, se suelen redondear o truncar (cortar) a un número específico de cifras.

Partes de un número decimal

Un número decimal se divide en dos partes principales:

• La parte entera es el número que está a la izquierda de la coma. Es un número entero (puede ser positivo, negativo o cero).
• La parte decimal o fraccionaria es el número que está a la derecha de la coma. Representa un valor entre cero y uno.

• Ejemplo:
  • En el número 5,85, el "5" es la parte entera y el "85" es la parte decimal.

¿Cómo se escriben los números decimales?

En español, hay diferentes formas de escribir los números decimales, usando un signo para separar la parte entera de la decimal:

• El punto decimal (.): Se usa un punto. Es común en calculadoras, ordenadores y en algunos países como México.

* Ejemplo: 3.141592

• La coma decimal (,): Se usa una coma. Es la forma más común en la mayoría de los países de habla hispana.

* Ejemplo: 3,141592

• El apóstrofo decimal ('): A veces se usa un apóstrofo. Aunque se entiende, no es la forma correcta según las reglas del idioma.

* Ejemplo: 3'141592

Las cifras después del separador decimal se escriben siempre juntas, sin espacios ni otros signos.

Valor de las cifras decimales

Cada posición después de la coma tiene un valor específico:

• La primera cifra después de la coma son las décimas (1/10).
• La segunda cifra son las centésimas (1/100).
• La tercera cifra son las milésimas (1/1000).
• Y así sucesivamente.

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{lcrcccl} \hline \rm d\acute{e}cima & \longmapsto & 10^{-1} & = & \cfrac{1}{10} & = & 0,1 \\ \rm cent\acute{e}sima & \longmapsto & 100^{-1} & = & \cfrac{1}{100} & = & 0,01 \\ \rm mil\acute{e}sima & \longmapsto & 1\,000^{-1} & = & \cfrac{1}{1\,000} & = & 0,001 \\ \rm diezmil\acute{e}sima & \longmapsto & 10\,000^{-1} & = & \cfrac{1}{10\,000} & = & 0,0001 \\ \rm cienmil\acute{e}sima & \longmapsto & 100\,000^{-1} & = & \cfrac{1}{100\,000} & = & 0,00001 \\ \rm millon\acute{e}sima & \longmapsto & 1\,000\,000^{-1} & = & \cfrac{1}{1000000\,} & = & 0,000001 \\ \hline \end{array}

Aproximación de números decimales

A veces, necesitamos redondear o truncar un número decimal para que sea más fácil de usar o para que tenga una precisión específica.

• El número 0,080 tiene tres cifras decimales y nos dice que la precisión llega hasta las milésimas (80 milésimas).
• El número 0,08 tiene dos cifras decimales y nos dice que la precisión llega hasta las centésimas (8 centésimas).

Aunque ambos representan la misma cantidad, la forma en que se escriben puede indicar el nivel de exactitud.

¿Los números decimales son únicos?

La forma en que escribimos algunos números decimales no es única. Por ejemplo, el número 1 se puede escribir como 1,0 o también como 0,999... (donde el 9 se repite infinitamente). Esto significa que 0,999... es exactamente igual a 1.

• Otros ejemplos:
  • 0,5 es igual a 0,499999...

Galería de imágenes

• 

  La escritura decimal de los números reales no es única, se puede demostrar que 0,999...=1.

Véase también

• Separador decimal
• Sistema de numeración decimal
• 0,9 periódico

Clasificación de los números Complejos Reales Racionales Enteros Naturales uno: 1 Naturales primos Naturales compuestos Cero: 0 Enteros negativos Fraccionarios Exactos Periódicos Puros Mixtos Irracionales Irracionales algebraicos Trascendentes Imaginarios