División por cero para niños
En matemáticas, la división entre cero es una operación en la que intentamos dividir un número por cero. El resultado de esta operación no está definido de una manera clara o única. En la aritmética y el álgebra, se considera que no tiene una solución posible, y si se usa mal, puede llevar a resultados que parecen correctos pero son falsos, como si 1 fuera igual a 2.
En el análisis matemático, a veces nos encontramos con situaciones donde un número se acerca mucho a cero en una división. Aunque en algunos casos esto se llama "indeterminación", a veces podemos entender qué sucede con el resultado.
Este problema de la división entre cero surgió hace mucho tiempo, alrededor del año 650, cuando en la India se empezó a usar más el concepto del cero y los números negativos. El primer matemático en hablar de esto fue el indio Bhaskara I, quien en el siglo VII escribió que un número dividido por cero era como el infinito.
Contenido
¿Por qué no se puede dividir entre cero?
En aritmética y álgebra
En los números naturales, enteros y reales, la división entre cero no tiene un valor específico. Esto se debe a una regla muy importante: cualquier número multiplicado por cero siempre da cero. Por ejemplo, 5 x 0 = 0, y 100 x 0 = 0.
Imagina que quieres dividir 8 entre 0. Estarías buscando un número que, al multiplicarlo por 0, te dé 8. Pero como ya sabemos, cualquier número multiplicado por 0 siempre es 0, ¡nunca 8! Por eso, no hay ningún número que sea la respuesta a 8 dividido por 0.
Ahora, ¿qué pasa si intentamos dividir 0 entre 0? Aquí el problema es diferente. Si buscas un número que, al multiplicarlo por 0, te dé 0, ¡hay infinitas posibilidades! Cualquier número funciona, porque 0 multiplicado por cualquier número siempre es 0. Como no hay una única respuesta, decimos que 0 dividido por 0 también es indefinido.
El algoritmo de la división
La división es como repartir algo en partes iguales. Por ejemplo, si tienes 12 galletas y las divides entre 3 amigos, cada uno recibe 4 galletas. Esto funciona porque 3 veces 4 es 12.
Pero si intentas dividir un número, como 2, entre 0, es como si quisieras repartir 2 galletas entre 0 amigos. No tiene sentido, ¿verdad? O, si lo vemos como restas repetidas, intentarías quitar 0 de 2 una y otra vez:
- 2 - 0 = 2
- 2 - 0 = 2
- 2 - 0 = 2...
Nunca terminarías de restar, porque el número 2 nunca cambiaría. Por eso, la división entre cero no es posible.
Errores matemáticos (falacias)
Una razón muy importante para no permitir la división por cero es que si lo hacemos, podemos llegar a conclusiones falsas o absurdas.
Por ejemplo, sabemos que:
- 0 multiplicado por 1 es igual a 0 (0 × 1 = 0)
- 0 multiplicado por 2 es igual a 0 (0 × 2 = 0)
Entonces, podemos decir que 0 × 1 = 0 × 2. Si intentáramos dividir ambos lados de esta igualdad por 0, obtendríamos:
- (0 × 1) / 0 = (0 × 2) / 0
- Lo que nos llevaría a: 1 = 2
¡Esto es un error! Sabemos que 1 no es igual a 2. Este ejemplo nos muestra por qué la división por cero no está permitida en las matemáticas.
A veces, este error puede estar escondido en problemas de álgebra. Por ejemplo, si tenemos una ecuación donde sin darnos cuenta dividimos por una expresión que vale cero, podemos llegar a un resultado incorrecto.
La división por cero en el análisis matemático
En el análisis matemático, que estudia cómo cambian las funciones, la división por cero se ve de otra manera, usando el concepto de límite.
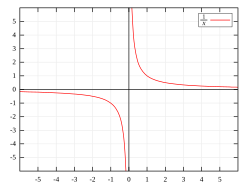
Imagina la función f(x) = n/x, donde n es un número positivo. Si intentamos calcular f(0) = n/0, la función no está definida en ese punto. Pero podemos ver qué pasa cuando x se acerca mucho a 0.
- Si x se acerca a 0 desde números positivos (por ejemplo, 0.1, 0.01, 0.001), el resultado de n/x se hace cada vez más grande, acercándose al infinito positivo.
- Si x se acerca a 0 desde números negativos (por ejemplo, -0.1, -0.01, -0.001), el resultado de n/x se hace cada vez más pequeño (más negativo), acercándose al infinito negativo.
Como los resultados se van a direcciones opuestas (uno a infinito positivo y otro a infinito negativo), decimos que la función no tiene un límite único en 0.
La división por cero en la informática
En el mundo de la informática y la programación, una división por cero es un error lógico muy conocido.
Muchos programas de computadora realizan divisiones usando el método de restas repetidas. Si el divisor es cero, el programa intentaría restar cero una y otra vez, sin que el número original cambie. Esto haría que el programa entrara en un bucle infinito, es decir, se quedaría repitiendo la misma acción sin parar, y el programa se "colgaría" o dejaría de funcionar.
Para evitar esto, los procesadores de las computadoras actuales están diseñados para detectar cuando ocurre una división por cero. Cuando esto pasa, el procesador envía un mensaje de error al sistema, y el programa que estaba ejecutándose se detiene para evitar problemas mayores.
Los programas que se usan para crear otros programas (llamados compiladores) también pueden avisar si detectan una división por cero. Algunos lenguajes de programación tienen formas especiales de "manejar excepciones", lo que significa que pueden detectar este error y ejecutar un código específico para solucionarlo o informarlo al usuario de una manera más amigable.
En el caso de los cálculos con números decimales (llamados de "coma flotante"), un estándar informático dice que si se divide por cero, el resultado debe ser "Inf" (que significa infinito) o "NaN" (que significa "No es un Número").
Véase también
 En inglés: Division by zero Facts for Kids
En inglés: Division by zero Facts for Kids
- Bien definido
- Forma indeterminada