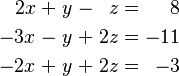Álgebra lineal para niños

El espacio euclídeo tridimensional R³ es un espacio vectorial y las líneas y los planos que pasan por el origen son subespacios vectoriales de R³.

El álgebra lineal es una parte de las matemáticas que estudia conceptos importantes como los vectores, las matrices y los sistemas de ecuaciones lineales. También se enfoca en los espacios vectoriales y las transformaciones lineales.

En otras palabras, el álgebra lineal se encarga de las ecuaciones lineales, que son como rompecabezas matemáticos donde buscamos valores desconocidos. También estudia las formas en que estas ecuaciones se representan usando matrices y espacios vectoriales.

Esta rama de las matemáticas es muy importante en casi todas las áreas de las matemáticas. Por ejemplo, ayuda a entender la geometría y a definir cosas básicas como líneas, planos y rotaciones. También es clave en el análisis funcional, que aplica ideas del álgebra lineal a los espacios de funciones.

El álgebra lineal se usa mucho en la mayoría de las ciencias y en la ingeniería. Permite crear modelos matemáticos para entender muchos fenómenos naturales y hacer cálculos de forma eficiente. Incluso para sistemas más complejos que no son lineales, el álgebra lineal se usa para hacer aproximaciones y entender cómo cambian las cosas.

La historia del álgebra lineal moderna comenzó en 1843. En ese año, William Rowan Hamilton inventó los cuaterniones, inspirándose en los números complejos. Él fue quien empezó a usar el término vector. Un año después, en 1844, Hermann Grassmann publicó su libro Die lineare Ausdehnungslehre, que significa "La teoría lineal de extensión".

Historia del Álgebra Lineal

Orígenes Antiguos

El método para resolver ecuaciones lineales que hoy conocemos como eliminación gaussiana ya se usaba hace mucho tiempo. Aparece en un texto matemático chino llamado Los nueve capítulos sobre el arte matemático. En su octavo capítulo, "Matrices rectangulares", se explica cómo usarlo para resolver problemas con varias ecuaciones.

En Europa, los Sistemas de ecuaciones lineales empezaron a estudiarse más a fondo en 1637. Fue cuando René Descartes introdujo las coordenadas en la geometría. Gracias a esta nueva forma de ver la geometría, llamada geometría cartesiana, las líneas y los planos se podían representar con ecuaciones lineales. Resolver dónde se cruzaban estas líneas y planos significaba resolver sistemas de ecuaciones lineales.

Los primeros métodos para resolver estos sistemas usaban determinantes. Leibniz los mencionó por primera vez en 1693. En 1750, Gabriel Cramer los usó para dar soluciones claras a los sistemas lineales, lo que hoy se conoce como la regla de Cramer. Más tarde, Gauss mejoró el método de eliminación, que al principio fue un gran avance en la geodesia.

El Nacimiento del Álgebra Lineal Moderna

En 1844, Hermann Grassmann publicó su "Teoría de la Extensión". Este libro incluía ideas nuevas que son la base de lo que hoy llamamos álgebra lineal. En 1848, James Joseph Sylvester usó por primera vez la palabra matriz. En latín, esta palabra significa "vientre".

El álgebra lineal siguió creciendo con ideas relacionadas con los números complejos. Por ejemplo, la diferencia entre dos números complejos se puede ver como un vector. En 1843, se creó el sistema de cuaterniones, que es como una extensión de los números complejos. Aquí, el término vector se usó para representar un punto en el espacio.

Arthur Cayley introdujo la multiplicación matricial y la matriz inversa en 1856. Esto hizo posible el grupo lineal general. Cayley fue muy importante porque usó una sola letra para representar una matriz, tratándola como un objeto completo. También vio la conexión entre las matrices y los determinantes.

Benjamin Peirce publicó su Álgebra lineal asociativa en 1872, y su hijo Charles Sanders Peirce continuó su trabajo.

La necesidad de entender fenómenos como el campo de fuerzas en la electricidad y el magnetismo impulsó el desarrollo del álgebra lineal. Esta rama de las matemáticas es como la geometría plana de la geometría diferencial y ayuda a entender las simetrías del espacio-tiempo.

La primera definición moderna y precisa de un espacio vectorial la dio Peano en 1888. Para 1900, ya existía una teoría de las transformaciones lineales para espacios vectoriales de tamaño finito. El álgebra lineal tomó su forma actual en la primera mitad del siglo XX. Muchas ideas antiguas se unieron en lo que se conoce como álgebra abstracta. Con la llegada de los ordenadores, se investigaron algoritmos más rápidos para la eliminación gaussiana y las descomposiciones de matrices. Así, el álgebra lineal se convirtió en una herramienta esencial para crear modelos y hacer simulaciones.

¿Qué es el Álgebra Lineal?

De forma más formal, el álgebra lineal estudia conjuntos especiales llamados espacios vectoriales. Estos conjuntos tienen vectores y escalares (números) que se pueden sumar y multiplicar de ciertas maneras.

También estudia las transformaciones lineales. Estas son funciones que conectan espacios vectoriales y mantienen sus propiedades de linealidad. Por ejemplo, si sumas dos vectores y luego aplicas la transformación, el resultado es el mismo que si aplicas la transformación a cada vector por separado y luego los sumas.

A diferencia de los ejemplos sencillos, los vectores no siempre son solo listas de números. Pueden ser elementos de cualquier conjunto, y a partir de ellos se puede construir un espacio vectorial.

Finalmente, el álgebra lineal también analiza propiedades adicionales que se pueden añadir a los espacios vectoriales. Una de las más comunes es el producto interno. Este "producto" entre dos vectores permite calcular la longitud de los vectores y el ángulo entre ellos.

Conceptos Clave del Álgebra Lineal

Vectores: Flechas con Dirección y Magnitud

Un vector es como una flecha que tiene una dirección y una longitud (magnitud). Los vectores se usan para representar cosas que tienen ambas características, como la velocidad de un coche o la fuerza que empuja un objeto.

Espacios Vectoriales: Donde Viven los Vectores

Un espacio vectorial es un conjunto de vectores donde se pueden hacer dos operaciones básicas:

• Suma de vectores: Si sumas dos vectores, el resultado es otro vector dentro del mismo espacio.
• Multiplicación por un escalar: Si multiplicas un vector por un número (un escalar), el resultado es otro vector dentro del mismo espacio.

Estas operaciones deben seguir ciertas reglas, como que la suma de vectores es asociativa y conmutativa. También debe existir un "vector cero" que, al sumarse a cualquier vector, no lo cambia.

Matrices: Tablas de Números para Organizar Información

Una matriz es una tabla rectangular de números, símbolos o expresiones. Se usan para organizar información y son muy importantes en el álgebra lineal, la ciencia y la ingeniería.

Las matrices nos permiten trabajar con espacios vectoriales de tamaño finito y con las transformaciones lineales. Por eso, entender las matrices es fundamental en el álgebra lineal.

La multiplicación de matrices se define de una manera especial. Cuando multiplicas dos matrices, el resultado es una matriz que representa la combinación de las transformaciones lineales que cada matriz representa.

Sistemas de Ecuaciones Lineales: Resolviendo Problemas con Muchas Incógnitas

Un sistema de ecuaciones lineales es un grupo de ecuaciones lineales con varias incógnitas. Resolver estos sistemas es una parte muy importante del álgebra lineal. Históricamente, el álgebra lineal y la teoría de matrices se desarrollaron para encontrar soluciones a estos sistemas.

Por ejemplo, un sistema de ecuaciones puede verse así:

Podemos usar la eliminación gaussiana para resolver estos sistemas. Este método consiste en hacer operaciones en las filas de la matriz que representa el sistema para simplificarlo y encontrar los valores de las incógnitas.

Transformaciones Lineales: Cambiando Formas de Manera Ordenada

Las transformaciones lineales son como "mapas" o "funciones" que toman un vector de un espacio y lo convierten en un vector de otro espacio (o del mismo). Lo hacen de una manera que respeta las operaciones de suma y multiplicación por un escalar.

Por ejemplo, una transformación lineal puede rotar un vector, estirarlo o reflejarlo. Si una transformación lineal es "biyectiva" (es decir, cada vector del segundo espacio se asocia con uno y solo uno del primero), se llama isomorfismo. Esto significa que los dos espacios vectoriales son "esencialmente iguales" desde el punto de vista del álgebra lineal.

Valores y Vectores Propios: Claves para Entender los Cambios

Si tenemos una transformación lineal que mapea un espacio vectorial a sí mismo, un vector propio es un vector especial que, cuando se le aplica la transformación, solo cambia su longitud, no su dirección. El número por el que se multiplica su longitud se llama valor propio.

Estos conceptos son muy importantes para entender cómo se comportan las transformaciones y las matrices. Nos ayudan a simplificar problemas complejos y a entender las propiedades de los sistemas.

Ejemplos de Espacios Vectoriales Comunes

Vectores en el Plano y el Espacio (Rⁿ)

Uno de los espacios vectoriales más conocidos es el conjunto de vectores de "n" dimensiones. Por ejemplo, en [[R²]], los vectores tienen dos componentes, como (2,3) o (3,4). Estos se usan para representar coordenadas cartesianas en un plano. En [[R³]], los vectores tienen tres componentes y se usan para el espacio tridimensional.

Polinomios: Álgebra Lineal con Expresiones Matemáticas

Otro ejemplo de espacio vectorial es el conjunto de todos los polinomios de un cierto grado (por ejemplo, grado 2 o menos) con números reales.

Algunos ejemplos de estos polinomios son:

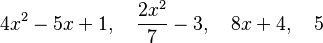
Si sumamos dos polinomios de este tipo, el resultado es otro polinomio del mismo tipo. También podemos multiplicar un polinomio por un número, y el resultado seguirá siendo un polinomio.

Una transformación lineal interesante en este espacio es la derivada. Si aplicamos la derivada a un polinomio, obtenemos otro polinomio. Por ejemplo:

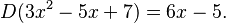
¿Para Qué Sirve el Álgebra Lineal?

El álgebra lineal se usa en casi todas las áreas de las matemáticas y, por lo tanto, en muchas ciencias. Aquí te mostramos algunas de sus aplicaciones:

En la Geometría y el Espacio

El álgebra lineal es fundamental para entender la geometría. Desde que René Descartes introdujo las coordenadas cartesianas en 1637, los puntos, líneas y planos se pueden describir con números y ecuaciones lineales. Esto permite calcular dónde se cruzan las líneas o los planos, lo cual es muy útil.

Muchas transformaciones geométricas, como las traslaciones (mover algo), rotaciones (girar algo) o reflexiones (ver algo como en un espejo), se pueden estudiar usando transformaciones lineales. Esto es muy importante en campos como la robótica, donde se necesita describir el movimiento de los brazos de un robot, o en los gráficos por ordenador, para crear imágenes en 3D.

En la Ciencia y la Ingeniería

El álgebra lineal es esencial para modelar muchos fenómenos físicos. Por ejemplo, en la predicción meteorológica, la atmósfera se divide en pequeñas "celdas". Las interacciones entre estas celdas se modelan con ecuaciones lineales, lo que permite predecir el tiempo. También se usa en la mecánica, la geodesia (para describir la forma de la Tierra) y la Visión artificial.

En la Computación

Casi todos los cálculos científicos que hacen los ordenadores usan álgebra lineal. Por eso, los algoritmos de álgebra lineal están muy optimizados para ser rápidos y eficientes. Programas como BLAS y LAPACK son ejemplos de esto.

Algunos procesadores, como las Unidad de procesamiento gráfico (GPU), están diseñados específicamente para hacer operaciones de álgebra lineal de forma muy rápida. Esto es crucial para los gráficos por ordenador, los videojuegos y la inteligencia artificial.

Véase también

En inglés: Linear algebra Facts for Kids