Producto escalar para niños
En matemáticas, el producto escalar, también conocido como producto interno o producto punto, es una operación especial que se hace con dos vectores. El resultado de esta operación es un número simple (un escalar), no otro vector.
Imagina que tienes dos flechas (vectores) en un espacio. El producto escalar te ayuda a entender cómo se relacionan estas flechas entre sí. Por ejemplo, te permite calcular la longitud de una flecha, el ángulo entre dos flechas, o si son completamente perpendiculares (forman un ángulo de 90 grados).
El producto escalar es muy útil en la geometría euclídea, que es la geometría que estudiamos normalmente en el colegio, donde las figuras son planas o tridimensionales.
Contenido
¿Qué es el Producto Escalar?
El producto escalar es una forma de "multiplicar" dos vectores para obtener un número. Este número nos da información sobre la relación entre esos vectores. Se llama "producto punto" porque se usa un punto (·) para representarlo, como en u · v. También se le llama "producto escalar" porque el resultado es un escalar (un número), a diferencia de otras operaciones que pueden dar como resultado otro vector.
¿Cómo se calcula el Producto Escalar?
El producto escalar se puede calcular de dos maneras principales: usando las coordenadas de los vectores o usando sus propiedades geométricas.
Cálculo con Coordenadas
Si tienes dos vectores, por ejemplo, u y v, y conoces sus coordenadas, puedes calcular su producto escalar.
Supongamos que el vector u tiene coordenadas (u1, u2, ..., un) y el vector v tiene coordenadas (v1, v2, ..., vn). Para calcular su producto escalar, multiplicas las coordenadas que están en la misma posición y luego sumas todos esos resultados.
Por ejemplo, si u = (1, 2, 3) y v = (4, 5, 6), el producto escalar sería: u · v = (1 * 4) + (2 * 5) + (3 * 6) u · v = 4 + 10 + 18 u · v = 32
Esta forma de calcularlo es muy común en el espacio euclídeo, que es el espacio que usamos para representar puntos y objetos en 2D o 3D.
Cálculo usando Matrices
También puedes pensar en los vectores como matrices de una sola columna. Si tienes el vector u como una matriz columna, puedes "voltearla" (hacer su transpuesta) para que sea una matriz fila. Luego, multiplicas esta matriz fila por la matriz columna del segundo vector. El resultado es el mismo que sumar los productos de las coordenadas.
Definición Geométrica del Producto Escalar
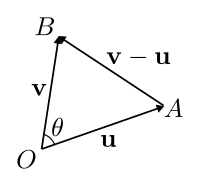
Si conoces la longitud (o "módulo") de los vectores y el ángulo que forman entre sí, puedes calcular el producto escalar de otra manera.
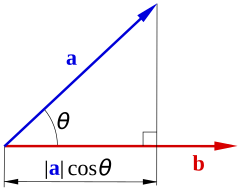
El módulo de un vector es su longitud. Se representa con dos barras verticales, como ||a||. Si a y b son dos vectores, y θ (theta) es el ángulo entre ellos, el producto escalar se define como: a · b = ||a|| * ||b|| * cos(θ)
Aquí, "cos(θ)" es el coseno del ángulo θ. El coseno es una función matemática que relaciona los ángulos de un triángulo con las longitudes de sus lados.
Propiedades Importantes del Producto Escalar
El producto escalar nos ayuda a entender varias características de los vectores:
¿Cómo se calcula la longitud de un vector?
La longitud o "módulo" de un vector se puede calcular usando el producto escalar. Si multiplicas un vector por sí mismo (producto escalar), el resultado es el cuadrado de su longitud.
Por ejemplo, si tienes un vector U, su longitud al cuadrado es: U · U = U₁² + U₂² + ... + Un²
Donde U₁, U₂, etc., son las coordenadas del vector. Para obtener la longitud real, solo tienes que calcular la raíz cuadrada de este resultado. ||U|| = √(U · U)
Un vector que tiene una longitud de 1 se llama vector unitario. Son muy útiles porque solo indican una dirección.
¿Cómo se encuentra el ángulo entre dos vectores?
Gracias a la definición geométrica, podemos usar el producto escalar para encontrar el ángulo entre dos vectores. Si conoces el producto escalar de dos vectores y sus longitudes, puedes despejar el coseno del ángulo:
cos(θ) = (u · v) / (||u|| * ||v||)
Si el resultado del producto escalar es positivo, el ángulo entre los vectores es menor de 90 grados. Si es negativo, el ángulo es mayor de 90 grados.
¿Cuándo son los vectores perpendiculares?
Dos vectores son ortogonales (o perpendiculares) si forman un ángulo de 90 grados entre sí. En este caso, el coseno de 90 grados es 0.
Por lo tanto, si el producto escalar de dos vectores es cero, significa que son perpendiculares. A · B = 0 significa que A es perpendicular a B.
¿Cuándo son los vectores paralelos?
Dos vectores son paralelos si apuntan en la misma dirección (ángulo de 0 grados) o en direcciones opuestas (ángulo de 180 grados).
Si el ángulo es 0 grados, el coseno es 1. Si el ángulo es 180 grados, el coseno es -1. En ambos casos, el valor absoluto del producto escalar es igual al producto de sus longitudes. |A · B| = ||A|| * ||B||
¿Qué es la Proyección de un Vector?
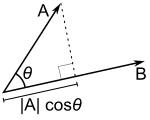
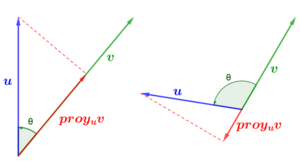
Imagina que tienes un vector (una flecha) y una línea. La proyección de ese vector sobre la línea es como la sombra que el vector proyecta sobre esa línea si la luz viniera de arriba. Es el componente del vector que va en la misma dirección que la línea.
El producto escalar te ayuda a calcular esta proyección. La proyección de un vector u sobre la dirección de un vector v se calcula así:
Proyección de u sobre v = (( u · v ) / ( v · v )) * v
Esto significa que el producto escalar de dos vectores también se puede ver como el producto de la longitud de uno de ellos por la longitud de la proyección del otro sobre él.
Propiedades Generales del Producto Interno
El producto escalar tiene varias propiedades importantes que lo hacen útil en matemáticas:
- Conmutatividad: En espacios reales, el orden de los vectores no importa. A · B es lo mismo que B · A.
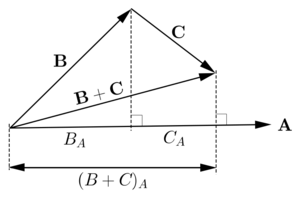
- Distributividad: Se puede "distribuir" sobre la suma de vectores. Por ejemplo, A · (B + C) = (A · B) + (A · C).
- Positividad: El producto escalar de un vector consigo mismo siempre es un número positivo o cero. Solo es cero si el vector es el vector nulo (un vector sin longitud).
- Desigualdad de Cauchy-Bunyakovsky-Schwarz: Esta es una propiedad muy importante que dice que el valor absoluto del producto escalar de dos vectores es siempre menor o igual que el producto de sus longitudes. Esto es lo que nos permite definir el ángulo entre vectores.
El Producto Escalar en el Espacio Tridimensional
En el espacio tridimensional (como el mundo en el que vivimos, con largo, ancho y alto), si tienes dos vectores U = (U₁, U₂, U₃) y V = (V₁, V₂, V₃), su producto escalar se calcula como:
U · V = (U₁ * V₁) + (U₂ * V₂) + (U₃ * V₃)
Esta es la forma más común de usar el producto escalar en problemas de física o ingeniería.
Véase también
 En inglés: Dot product Facts for Kids
En inglés: Dot product Facts for Kids
- Multiplicación escalar
- Espacio vectorial
- Norma vectorial
- Producto vectorial