Raíz de un polinomio para niños
En matemáticas, una raíz de un polinomio P(X) es un valor α tal que P(α) = 0. Por lo tanto, es una solución de la ecuación polinómica P(x) = 0 para la incógnita x, o también un cero de la función polinómica asociada.
Un polinomio distinto de cero con coeficientes en un determinado cuerpo puede tener raíces solo en un cuerpo «más grande», pero nunca tiene un número de raíces mayor que su grado. Por ejemplo (X2 - 2 = 0), que es de grado 2 y con coeficientes racionales, no tiene raíces racionales, pero tiene dos raíces en los números reales ℝ (y por lo tanto, también en los números complejos ℂ). El teorema fundamental del álgebra indica que cualquier polinomio de grado n con coeficientes complejos admite n raíces complejas (no necesariamente distintas).
La noción de raíz se generaliza, bajo el nombre de cero, a un polinomio de varias variables.
Contenido
Definiciones
Considérese un polinomio P(X) con una variable denotada comoX, con coeficientes en un cuerpo o más generalmente en un anillo conmutativo A (los coeficientes pueden por lo tanto pertenecer a un subanillo).
Definición
|
Así, el polinomio (X2 - 2 = 0), con coeficientes en ℚ (y por lo tanto, también en ℝ o ℂ), no tiene ninguna raíz en ℚ pero tiene dos en ℝ (√2 y –√2) (y por lo tanto, también en ℂ). De hecho, si se sustituye √2 o –√2 por X en el polinomio, se obtiene 0.
Etimología: El término raíz proviene de las traducciones latinas de Robert de Chester y Gerardo de Cremona del término gizr. La palabra gizr significa 'raíz', y se traduce al latín como radix. El término gizr es utilizado por el matemático de origen persa del siglo VIII Al-Juarismi, en su tratado Kitâb al-jabr wa al-muqâbala, obra que se ocupó por primera vez de forma exhaustiva del cálculo de las raíces reales de la ecuación de segundo grado.
Definición alternativa
|
De hecho, si P(X) = (X - α) Q(X), entonces P(α) = 0 y viceversa, si P(α) = 0 entonces P(X) es igual a P(X) - P(α), combinación lineal de polinomios de la forma Xk - αk, todos divisibles por X – α.
En el ejemplo elegido, la igualdad:
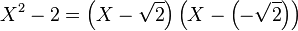
es otra forma de denotar que √2 y –√2 son de hecho las dos raíces del polinomio.
Definiciones relacionadas
El simple hecho de que el polinomio (X - α) sea unitario permite (sin necesidad de asumir la integridad en A) definir las siguientes nociones:
|
El polinomio (X2 - 2) es separable, es decir, no tiene raíces múltiples. Además, se divide en ℝ, en el siguiente sentido:
|
P es entonces distinto de cero, y su coeficiente dominante es el producto de los coeficientes dominantes de estos polinomios de primer grado. De manera más general, se dice que un polinomio distinto de cero de L[X] se divide en L si es el producto de una constante y un producto (que puede ser vacío) de polinomios unitarios de primer grado. Tal descomposición es entonces única: cada término constante de uno de estos polinomios unitarios de primer grado es igual al opuesto de una raíz de P en L, y si esta raíz es de orden m, este factor se repite m veces. Por lo tanto, el número de estos factores es igual al grado de P.
Existencia de raíces
|
Este es una aplicación del teorema del valor intermedio.
Sea K un cuerpo conmutativo y P un polinomio con una variable y con coeficientes en K.
Una extensión de K es un cuerpo que contiene a K; por tanto, ℝ y ℂ son extensiones de ℚ.
Surge una pregunta natural: si L1 y L2 son dos extensiones de K en las que se divide P, las raíces, vistas como elementos de L1, ¿son "equivalentes" a las raíces vistas como elementos de L2? Esta equivalencia existe: existe en L1 una sub-extensión "más pequeña", llamada cuerpo de descomposición de P, que contiene todas las raíces de P, e igualmente en L2 , y estas dos sub-extensiones de K son idénticas. En el ejemplo K = ℚ, P = X2 - 2, este cuerpo de descomposición es el conjunto de números de la forma a + b √2, donde a y b son números racionales. Este conjunto está identificado (por un isomorfismo no único) con un cuerpo único de ℝ y del cuerpo ℚ de números algebraicos. Así, el par de raíces (√2, –√2) incluido en ℝ puede considerarse idéntico al incluido en ℚ.
|
El cuerpo L es tal que el polinomio P está dividido; por otro lado, otros polinomios con coeficientes en K no necesariamente se dividen en L. A fortiori, un polinomio con coeficientes en L tampoco se divide necesariamente en L. Se dice que un cuerpo L es algebraicamente cerrado si todo polinomio con coeficientes en L se divide en L.
|
El cuerpo ℂ está algebraicamente cerrado, un resultado conocido como teorema fundamental del álgebra. El cierre algebraico de ℝ es ℂ. El de ℚ es el subcuerpo ℚ.
Criterio diferencial para la multiplicidad de una raíz
|
| Demostración |
| Por hipótesis, P(X) es de la forma (X – α)m Q(X) con m > 0 y Q(α) ≠ 0. Derivando, se obtiene P'(X) = (X – α)m–1R(X), con R(X) = mQ(X) + (X – α)Q'(X) y entonces R(α) = mQ(α), lo que prueba el primer punto. Los otros dos se deducen por inducción.
Otro método es usar la regla de Leibniz, que también se aplica a las derivadas formales. |
En particular:
- Una raíz de P es múltiple si y solo si también es raíz de P';
- Si A es un cuerpo de característica 0, entonces para que α sea una raíz de orden r de P, es necesario y suficiente que P(α), P'(α), P''(α),…, P(r–1) (α) sean cero y P(r)(α) no sea cero.
En un cuerpo de característica p> 0, este último criterio no es válido porque el polinomio derivado de Xp es nulo.
Relaciones entre los coeficientes y las raíces
Un polinomio  de grado
de grado  en un cuerpo K se escribe en su forma más general:
en un cuerpo K se escribe en su forma más general:
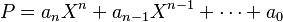
donde los 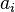 se denominan coeficientes de
se denominan coeficientes de 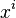 .
.
Si  está dividido, también es posible definirlo gracias a sus raíces, es decir, al conjunto de valores de
está dividido, también es posible definirlo gracias a sus raíces, es decir, al conjunto de valores de  que cancelan
que cancelan  . Así, el teorema fundamental del álgebra garantiza que cualquier polinomio de grado
. Así, el teorema fundamental del álgebra garantiza que cualquier polinomio de grado  con coeficientes complejos admite exactamente
con coeficientes complejos admite exactamente  raíces en
raíces en 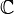 , posiblemente múltiples (en
, posiblemente múltiples (en 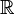 por otro lado, esto no siempre es cierto). De ello se deduce que un polinomio
por otro lado, esto no siempre es cierto). De ello se deduce que un polinomio  con coeficientes complejos se puede reescribir como:
con coeficientes complejos se puede reescribir como:
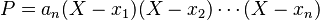 ,
,con 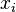 siendo las raíces de
siendo las raíces de  , que pueden ser múltiples. Las relaciones entre los coeficientes y las raíces llevan el nombre de François Viète, el primer matemático en enunciarlas en el caso de las raíces positivas.
, que pueden ser múltiples. Las relaciones entre los coeficientes y las raíces llevan el nombre de François Viète, el primer matemático en enunciarlas en el caso de las raíces positivas.
Relaciones de Viète
Polinomios simétricos
Se define el polinomio simétrico 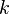 -ésimo, denotado de la forma
-ésimo, denotado de la forma 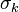 , como la suma de sus elementos multiplicada por
, como la suma de sus elementos multiplicada por 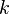 . Por ejemplo, los polinomios simétricos asociados a las variables
. Por ejemplo, los polinomios simétricos asociados a las variables 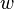 ,
,  ,
,  y
y 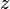 son:
son:
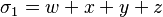 ,
,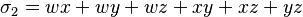 ,
,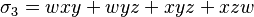 ,
,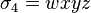 .
.
Más generalmente,
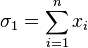 ,
,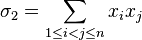 ,
,
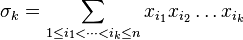 ,
,
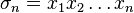 .
.
Teorema
Sea  un polinomio dividido de grado
un polinomio dividido de grado  y
y 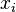 sus raíces
sus raíces  , que pueden ser múltiples. Entonces,
, que pueden ser múltiples. Entonces,
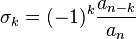 .
.Estas relaciones se prueban desarrollando el producto 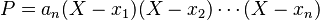 e identificando los coeficientes de expansión (que se expresan a partir de los polinomios simétricos de las raíces) con los coeficientes de
e identificando los coeficientes de expansión (que se expresan a partir de los polinomios simétricos de las raíces) con los coeficientes de 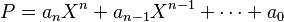 .
.
Ejemplos
- Caso
 . Sea
. Sea 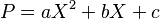 y sean
y sean 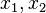 sus raíces. Entonces:
sus raíces. Entonces:
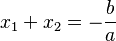 ,
,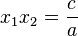 .
.
- Caso
 . Sea
. Sea 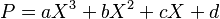 y sean sus raíces
y sean sus raíces 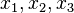 . Entonces,
. Entonces,
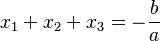 ,
,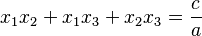 ,
,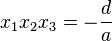 .
.
Sumas de Newton
Ejemplo introductorio
Sea el polinomio dado 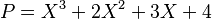 , con
, con  ,
,  , y
, y  sus raíces. Se desea determinar la suma
sus raíces. Se desea determinar la suma 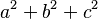 . Para ello, se dispone de la siguiente identidad:
. Para ello, se dispone de la siguiente identidad:
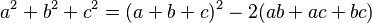 ,
,para que, según las relaciones de Viète:
 .
.Teorema
Las sumas de Newton son una generalización de este principio. Se establece 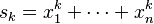 , donde
, donde 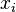 son las raíces de
son las raíces de 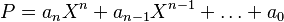 (en particular,
(en particular,  ). El método presentado en el ejemplo está generalizado, pero los cálculos se vuelven complicados. Por otro lado, se puede demostrar directamente que, para
). El método presentado en el ejemplo está generalizado, pero los cálculos se vuelven complicados. Por otro lado, se puede demostrar directamente que, para 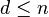 :
:
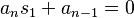 ,
,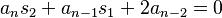 ,
,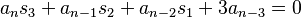 ,
,
 .
.
Continuidad de las raíces
Debido a su expresión polinomial, los coeficientes de un polinomio de coeficientes complejos son funciones continuas de sus raíces. Lo contrario es cierto pero más difícil de demostrar. Considérese la aplicación 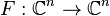 definida por:
definida por:
donde 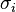 son los polinomios simétricos elementales definidos a partir de
son los polinomios simétricos elementales definidos a partir de 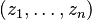 .
.
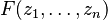 reúne la lista de los coeficientes de los polinomios mónicos
reúne la lista de los coeficientes de los polinomios mónicos 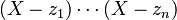 (excepto el coeficiente dominante igual a 1). Según el teorema fundamental del álgebra, esta aplicación es sobreyectiva. F es continua, ya que los coeficientes del polinomio son funciones continuas de las raíces. La factorización canónica de F conduce a la introducción de la siguiente relación de equivalencia en el conjunto inicial
(excepto el coeficiente dominante igual a 1). Según el teorema fundamental del álgebra, esta aplicación es sobreyectiva. F es continua, ya que los coeficientes del polinomio son funciones continuas de las raíces. La factorización canónica de F conduce a la introducción de la siguiente relación de equivalencia en el conjunto inicial  de F:
de F:
donde 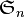 es el grupo simétrico en el conjunto
es el grupo simétrico en el conjunto 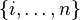 de los índices.
de los índices.
Ahora, se denota como 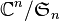 al conjunto cociente. Se dota al conjunto con una topología cociente. F se factoriza en la forma
al conjunto cociente. Se dota al conjunto con una topología cociente. F se factoriza en la forma  , donde
, donde  es la proyección canónica de
es la proyección canónica de  en
en 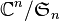 , y F}} la aplicación de
, y F}} la aplicación de 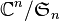 en
en  que, a una clase de equivalencia representada por
que, a una clase de equivalencia representada por 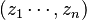 , asocia la secuencia de polinomios simétricos elementales correspondientes. Entonces, se puede demostrar que F es un homeomorfismo entre el conjunto
, asocia la secuencia de polinomios simétricos elementales correspondientes. Entonces, se puede demostrar que F es un homeomorfismo entre el conjunto 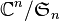 de las raíces del polinomio (salvo permutaciones) y el conjunto
de las raíces del polinomio (salvo permutaciones) y el conjunto  de los coeficientes del polinomio.
de los coeficientes del polinomio.
Cálculo de raíces
Se puede usar el método de Muller para calcular las raíces de un polinomio. Se interpola el polinomio P mediante un polinomio de grado dos: 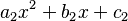 según el polígono interpolante de Lagrange. Los coeficientes se determinan evaluando P en tres puntos (
según el polígono interpolante de Lagrange. Los coeficientes se determinan evaluando P en tres puntos (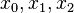 ):
):
con: ![f[u, v] = \frac{f(u) - f(v)}{u - v}.](/images/math/3/7/f/37fa6a4264ff74c8ce7cc9215d88dcaf.png)
Pero usando este polinomio de aproximación, la elección de la raíz de este polinomio es problemática. Müller tuvo entonces la idea de utilizar el mismo polinomio, pero en la forma: 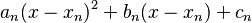 con
con 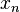 que tenderá hacia la raíz. Una característica especial de este algoritmo es que
que tenderá hacia la raíz. Una característica especial de este algoritmo es que 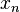 puede ser un número complejo. Coeficientes:
puede ser un número complejo. Coeficientes:
Este método es autoconvergente: el cálculo de la raíz se irá afinando poco a poco. Por lo tanto, se puede comenzar con  ,
, 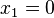 y
y 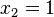 y
y  . Siempre que el polinomio no desaparezca en
. Siempre que el polinomio no desaparezca en 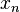 , se pasa a la siguiente iteración
, se pasa a la siguiente iteración  con:
con:
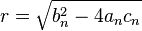 , donde
, donde 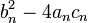 puede ser negativo o complejo.
puede ser negativo o complejo.
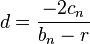 si
si 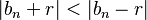
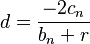 , o de lo contrario
, o de lo contrario
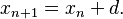
Finalmente, el cero es 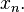
Véase también
 En inglés: Polynomial root Facts for Kids
En inglés: Polynomial root Facts for Kids
- Raíz de un polinomio real o complejo
- Incógnita
- Soluciones complejas de ecuaciones polinómicas con coeficientes reales
- Ecuación algebraica
- Función polinómica
- Método de Muller
- Teorema de Rouché


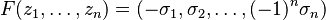
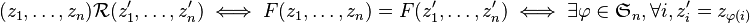
![a_2 = \frac{P[x_0, x_1] - P[x_1, x_2]}{x_0 - x_2} = P[x_0, x_1, x_2]](/images/math/f/5/4/f5497937dd6c199239699c880a6d300c.png)
![b_2 = P[x_1, x_2] - a_2\times (x_1 + x_2)](/images/math/4/3/d/43d3b480bb05eae2a8e1fc7dc3728d06.png)
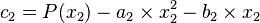
![a_n = P[x_{n-2}, x_{n-1}, x_n]](/images/math/c/2/0/c2078c4972cb9839cb79ee52c00f0e9e.png)
![b_n = P[x_{n-1}, x_n] - a_n\times (x_{n-1} - x_n)](/images/math/e/3/9/e39e05413ca428ddb3ae535b73e2220d.png)