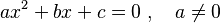Ecuación de segundo grado para niños
Una ecuación de segundo grado o ecuación cuadrática es un tipo de ecuación matemática que tiene una forma especial. Se llama "de segundo grado" porque la incógnita, que normalmente representamos con la letra x, está elevada al cuadrado (es decir, x2).
La forma general de una ecuación de segundo grado es:
|
Aquí, x es la variable o incógnita que queremos encontrar. Las letras a, b y c son números fijos, llamados coeficientes. Es muy importante que el número a no sea cero, porque si lo fuera, la ecuación dejaría de ser de segundo grado.
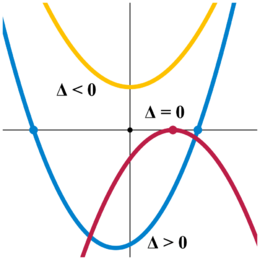
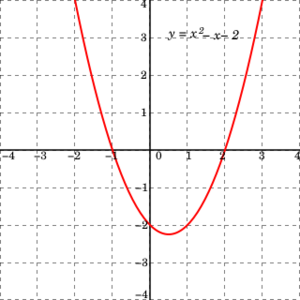
Podemos entender mejor estas ecuaciones si las dibujamos. La gráfica de una función cuadrática (que es lo que representa esta ecuación) siempre es una parábola, una curva con forma de "U" o "U" invertida. Cuando la parábola cruza el eje horizontal (eje Ox), los puntos donde lo hace nos dan las soluciones de la ecuación. Si la parábola no toca el eje Ox, las soluciones son números especiales llamados números complejos.
Contenido
Historia de las Ecuaciones Cuadráticas
Las ecuaciones de segundo grado se conocen desde hace mucho tiempo. Ya en la antigua Babilonia, hace miles de años, se usaban métodos para resolverlas. Estos métodos también se descubrieron de forma independiente en otras partes del mundo.
En Grecia, el matemático Diofanto de Alejandría propuso una manera de resolverlas, aunque su método solo encontraba una de las soluciones, incluso si había dos soluciones positivas. La primera solución completa y general fue desarrollada por el matemático Al-Juarismi en el siglo IX. Él escribió un libro muy importante llamado Compendio de cálculo por reintegración y comparación, donde explicó cómo resolver estas ecuaciones.
Más tarde, el matemático Abraham bar Hiyya, basándose en el trabajo de Al-Juarismi, también estudió estas soluciones en su libro Liber embadorum.
Un gran desafío en la historia de estas ecuaciones surgió con la ecuación 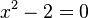 . Al intentar resolverla, los pitagóricos se dieron cuenta de que la raíz cuadrada de dos no podía expresarse como una fracción de dos números enteros.
. Al intentar resolverla, los pitagóricos se dieron cuenta de que la raíz cuadrada de dos no podía expresarse como una fracción de dos números enteros.
En el Renacimiento, al intentar resolver 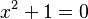 , se necesitaba un número que al elevarlo al cuadrado diera -1. Esto llevó a la creación de los números imaginarios y la unidad imaginaria i, definida como
, se necesitaba un número que al elevarlo al cuadrado diera -1. Esto llevó a la creación de los números imaginarios y la unidad imaginaria i, definida como 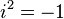 .
.
Cómo se Resuelven las Ecuaciones de Segundo Grado
Una ecuación cuadrática siempre tiene dos soluciones, que llamamos raíces. Estas soluciones pueden ser números reales (los que usamos normalmente) o números complejos.
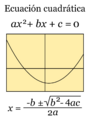
La forma más común y útil para encontrar las soluciones es usando la siguiente fórmula general:
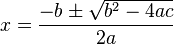
El símbolo "±" (más-menos) significa que hay dos soluciones posibles: una usando el signo de suma (+) y otra usando el signo de resta (-).
- La primera solución es:
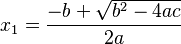
- La segunda solución es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_2 = \frac{-b - \sqrt {b^2-4ac}}{2a}
El Discriminante: ¿Qué tipo de soluciones tendremos?
La parte de la fórmula que está dentro de la raíz cuadrada, 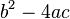 , es muy importante y se llama discriminante. Se representa con la letra griega delta (
, es muy importante y se llama discriminante. Se representa con la letra griega delta (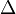 ). El valor del discriminante nos dice si las soluciones serán números reales o complejos, y si serán iguales o diferentes.
). El valor del discriminante nos dice si las soluciones serán números reales o complejos, y si serán iguales o diferentes.
- Si
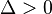 (el discriminante es positivo): La ecuación tiene dos soluciones reales y diferentes. Esto significa que la parábola corta el eje Ox en dos puntos distintos.
(el discriminante es positivo): La ecuación tiene dos soluciones reales y diferentes. Esto significa que la parábola corta el eje Ox en dos puntos distintos. - Si
 (el discriminante es cero): La ecuación tiene una única solución real, que se repite dos veces (se dice que tiene multiplicidad dos o es una raíz doble). La parábola solo toca el eje Ox en un único punto.
(el discriminante es cero): La ecuación tiene una única solución real, que se repite dos veces (se dice que tiene multiplicidad dos o es una raíz doble). La parábola solo toca el eje Ox en un único punto. - Si
 (el discriminante es negativo): La ecuación tiene dos soluciones complejas. En este caso, la parábola no corta el eje Ox.
(el discriminante es negativo): La ecuación tiene dos soluciones complejas. En este caso, la parábola no corta el eje Ox.
Métodos para Resolver Ecuaciones Cuadráticas
Además de la fórmula general, hay otras maneras de resolver estas ecuaciones:
Factorización por Inspección
A veces, una ecuación cuadrática como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ax^2 + bx + c = 0 se puede escribir como la multiplicación de dos expresiones más simples, por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (px + q)(rx + s) = 0 . Si logramos hacer esto, podemos encontrar las soluciones fácilmente.
Por ejemplo, la ecuación Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 + 5x + 6 = 0 se puede factorizar como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x + 3)(x + 2) = 0 . Para que esta multiplicación sea cero, uno de los paréntesis debe ser cero. Así, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x + 3 = 0 (lo que da  ) o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x + 2 = 0 (lo que da Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = -2 ). Estas son las soluciones.
) o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x + 2 = 0 (lo que da Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = -2 ). Estas son las soluciones.
Este método es útil cuando las soluciones son números sencillos, pero no funciona para todas las ecuaciones.
Completar el Cuadrado
Este método consiste en transformar la ecuación para que uno de sus lados sea un cuadrado perfecto, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x+h)^2 . Aquí te mostramos los pasos:
1. Divide toda la ecuación por el número a (el coeficiente de x2). 2. Mueve el término constante (el número sin x) al otro lado de la ecuación. 3. Suma a ambos lados de la ecuación el cuadrado de la mitad del coeficiente de x. Esto hace que el lado izquierdo se convierta en un cuadrado perfecto. 4. Escribe el lado izquierdo como un cuadrado y simplifica el lado derecho. 5. Toma la raíz cuadrada de ambos lados, recordando que hay una raíz positiva y una negativa. 6. Despeja x para encontrar las soluciones.
Veamos un ejemplo con Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2x^2 + 4x - 4 = 0 :
- Divide por 2: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 + 2x - 2 = 0
- Mueve el -2: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 + 2x = 2
- Suma el cuadrado de la mitad de 2 (que es 12 = 1): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 + 2x + 1 = 2 + 1
- Escribe como cuadrado: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x + 1)^2 = 3
- Toma la raíz cuadrada: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x + 1 = \pm\sqrt{3}
- Despeja x: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = -1 \pm\sqrt{3}
Esto nos da dos soluciones: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = -1 + \sqrt{3} y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = -1 - \sqrt{3} .
Ecuaciones Incompletas
A veces, una ecuación de segundo grado no tiene todos los términos.
Sin término independiente (sin c)
Son de la forma Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ax^2 + bx = 0 . Para resolverlas, puedes sacar factor común x: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x(ax + b) = 0 . Esto significa que una solución es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_1 = 0 , y la otra se obtiene de 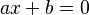 , que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_2 = \frac{-b}{a} .
, que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_2 = \frac{-b}{a} .
Sin término lineal (sin b)
Son de la forma Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ax^2 + c = 0 . Para resolverlas, despejas x2: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 = \frac{-c}{a} . Luego, tomas la raíz cuadrada: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = \pm\sqrt{\frac{-c}{a}} .
- Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{-c}{a} es un número positivo, las soluciones son dos números reales opuestos.
- Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{-c}{a} es un número negativo, las soluciones son dos números imaginarios opuestos.
Ecuación Bicuadrada
Una ecuación bicuadrada es un tipo especial de ecuación de cuarto grado (donde la x está elevada a la cuarta potencia, x4). Su forma es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ax^4 + {bx^2}^{} + c = 0
Para resolverla, se hace un truco: se cambia la variable. Si decimos que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): u = x^2 , entonces la ecuación se convierte en una ecuación de segundo grado con u: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {au^2}^{} + bu + c = 0
Puedes resolver esta nueva ecuación para encontrar los valores de u usando la fórmula general. Una vez que tengas los valores de u (digamos 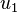 y
y 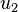 ), recuerda que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): u = x^2 . Así que, para encontrar x, debes tomar la raíz cuadrada de cada valor de u:
), recuerda que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): u = x^2 . Así que, para encontrar x, debes tomar la raíz cuadrada de cada valor de u:
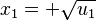
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_2 = -\sqrt{u_1}
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_3 = +\sqrt{u_2}
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_4 = -\sqrt{u_2}
Esto te dará las cuatro soluciones de la ecuación bicuadrada.
Relación con la Proporción Áurea
Un dato curioso es que la proporción áurea (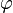 ), un número muy especial que aparece en la naturaleza y el arte, se puede obtener de una ecuación cuadrática. Si en la fórmula general de la ecuación de segundo grado usamos los valores
), un número muy especial que aparece en la naturaleza y el arte, se puede obtener de una ecuación cuadrática. Si en la fórmula general de la ecuación de segundo grado usamos los valores  , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b=-1 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c=-1 , una de las soluciones es precisamente la proporción áurea:
, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b=-1 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c=-1 , una de las soluciones es precisamente la proporción áurea:
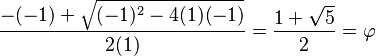
Galería de imágenes
Véase también
 En inglés: Quadratic equation Facts for Kids
En inglés: Quadratic equation Facts for Kids