Relación de equivalencia para niños

Una relación de equivalencia es una forma especial de conectar elementos dentro de un grupo o conjunto. Imagina que tienes un montón de objetos y quieres agruparlos según alguna característica que compartan. Por ejemplo, si tienes un grupo de amigos, podrías agruparlos por su edad, o por el color de su camiseta. Una relación de equivalencia nos ayuda a hacer estas agrupaciones de manera matemática.

Cuando usamos una relación de equivalencia, los elementos que están "relacionados" entre sí se consideran "equivalentes". Esto nos permite formar "paquetes" de elementos que son similares. Estos paquetes se llaman clases de equivalencia. Al final, podemos crear un nuevo conjunto donde cada paquete se trata como un solo elemento.

¿Qué es una Relación de Equivalencia?

Para que una conexión entre elementos sea una relación de equivalencia, debe cumplir tres reglas importantes. Piensa en un conjunto de cosas, al que llamaremos K, y una forma de relacionar sus elementos, que llamaremos R. La relación R es de equivalencia si cumple:

Reflexividad: ¿Está cada elemento relacionado consigo mismo?

Esta regla dice que cada elemento en el conjunto K siempre está relacionado consigo mismo.

• Por ejemplo, si la relación es "tener la misma edad que", entonces tú tienes la misma edad que tú mismo. Esto es obvio, ¿verdad?
• En matemáticas, lo escribimos así: para cualquier elemento x en K, x está relacionado con x.

Simetría: Si A se relaciona con B, ¿B se relaciona con A?

Esta regla significa que si un elemento x está relacionado con otro elemento y, entonces y también debe estar relacionado con x.

• Por ejemplo, si "Juan tiene la misma edad que María", entonces "María tiene la misma edad que Juan".
• En matemáticas: si x está relacionado con y, entonces y está relacionado con x.

Transitividad: Si A se relaciona con B, y B con C, ¿A se relaciona con C?

Esta regla dice que si un elemento x está relacionado con y, y y a su vez está relacionado con un tercer elemento z, entonces x también debe estar relacionado con z.

• Por ejemplo, si "Juan tiene la misma edad que María", y "María tiene la misma edad que Pedro", entonces "Juan tiene la misma edad que Pedro".
• En matemáticas: si x está relacionado con y, y y está relacionado con z, entonces x está relacionado con z.

Diagrama con los diferentes tipos de relaciones binarias, partiendo de la relación homogénea

¿Cómo se usa la notación?

En algunos casos, como en la aritmética modular, una relación de equivalencia entre dos números x e y se escribe como `x ≡ y (mod R)`. Esto se lee como "x es equivalente a y módulo R". Significa que x e y se comportan de manera similar cuando se dividen por R.

Clases de Equivalencia

Cuando tenemos una relación de equivalencia sobre un conjunto, podemos dividir ese conjunto en grupos especiales llamados clases de equivalencia.

• Imagina que tienes un conjunto de números enteros. Si la relación es "tener el mismo resto al dividir por 2", entonces los números pares (0, 2, 4, ...) forman una clase de equivalencia, y los números impares (1, 3, 5, ...) forman otra.
• Una clase de equivalencia para un elemento a incluye a todos los elementos que están relacionados con a. Se escribe como `[a]`.
• Al elemento a se le llama el representante de la clase.

Diagrama que muestra la estructura de una relación de equivalencia. Los puntos representan elementos y las flechas relaciones entre ellos

Conjunto Cociente

El conjunto cociente es el conjunto que se forma al reunir todas las clases de equivalencia. Es como si cada "paquete" de elementos similares se convirtiera en un solo "super-elemento" en este nuevo conjunto. Se denota como `K/R`.

Partición de un Conjunto

Una relación de equivalencia siempre divide un conjunto en partes que no se superponen y que, juntas, forman el conjunto original. Esto se llama una partición.

• Cada una de estas partes es una clase de equivalencia.
• Las clases de equivalencia son "disjuntas", lo que significa que no tienen elementos en común.
• La unión de todas las clases de equivalencia es igual al conjunto completo.

Esto es muy útil porque nos permite clasificar objetos o ideas en "tipos" basados en alguna característica compartida.

Historia de las Relaciones de Equivalencia

La idea de agrupar cosas por similitud no es nueva. Ya en la antigua Grecia, el matemático Euclides (alrededor del 300 a.C.) usaba ideas parecidas a las relaciones de equivalencia en su obra "Elementos de Euclides". Por ejemplo, al hablar de "proporcionalidad" o al clasificar figuras geométricas por su forma, estaba usando conceptos que hoy llamaríamos equivalencia.

Muchos siglos después, en 1801, el famoso matemático Carl Friedrich Gauss introdujo el concepto de "congruencia" en su libro "Disquisitiones arithmeticae". Él decía que dos números eran "congruentes" si su diferencia era un múltiplo de otro número. Esta definición es muy similar a la que usamos hoy para las relaciones de equivalencia, y la congruencia es un ejemplo perfecto de una.

Otros matemáticos importantes como Richard Dedekind y Georg Cantor también usaron relaciones de equivalencia en sus trabajos, aunque no las definieron formalmente al principio. Dedekind profundizó en la idea de congruencia de Gauss, y Cantor la usó para comparar el tamaño de conjuntos infinitos.

La definición formal de una relación de equivalencia, con sus tres propiedades (reflexiva, simétrica y transitiva), no apareció hasta 1912. Fue el matemático británico Philip Jourdain quien la presentó, llamándola "relación isoid". Sin embargo, no fue hasta 1929, con el libro "Höhere algebra" de Helmut Hasse, y más tarde con la obra de John W. Tukey en 1940, que la definición se estableció y se hizo ampliamente conocida en las matemáticas.

Ejemplos de Relaciones de Equivalencia

Las relaciones de equivalencia aparecen en muchos lugares de las matemáticas y en la vida diaria:

• La igualdad matemática: Cuando decimos que `1/2` es igual a `4/8`, estamos usando una relación de equivalencia.
• Cumplir años el mismo día que: Si la relación es "cumple años el mismo día que", todas las personas nacidas el 1 de enero forman una clase de equivalencia, las nacidas el 2 de enero forman otra, y así sucesivamente.
• Ser similar a (en geometría): En el conjunto de todos los triángulos, la relación "es similar a" (tienen la misma forma, aunque no el mismo tamaño) es una relación de equivalencia.
• Ser congruente con (en geometría): En el conjunto de todos los triángulos, la relación "es congruente con" (tienen la misma forma y el mismo tamaño) también es una relación de equivalencia.
• Congruencia módulo M: En los números enteros, si decimos que dos números están relacionados si su resta es un múltiplo de un número M (por ejemplo, M=2), entonces los números pares forman una clase y los impares otra.
• Tener el mismo valor absoluto que: En los números reales, `5` y `-5` tienen el mismo valor absoluto (`5`), por lo que están relacionados.
• Tener el mismo coseno que: En el conjunto de todos los ángulos, `0` grados y `360` grados tienen el mismo coseno (`1`), por lo que están relacionados.

Un ejemplo sencillo

Imagina un conjunto `X = {a, b, c}`. Podemos definir una relación `R` donde:

• `a` está relacionado con `a`
• `b` está relacionado con `b`
• `c` está relacionado con `c`
• `b` está relacionado con `c`
• `c` está relacionado con `b`

Esta es una relación de equivalencia. Las clases de equivalencia serían:

• `[a] = {a}` (solo `a` está relacionado consigo mismo)
• `[b] = {b, c}` (porque `b` está relacionado con `c`, y `c` con `b`)
• `[c] = {b, c}` (es la misma clase que `[b]`)

El conjunto de todas las clases de equivalencia es `{{a}, {b, c}}`. Este conjunto es una partición de `X`.

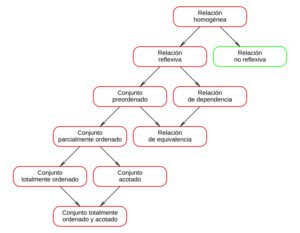
Conexiones con otras relaciones

• Una igualdad es un tipo especial de relación que es reflexiva, simétrica y antisimétrica (si `a` es igual a `b`, y `b` es igual a `a`, entonces `a` y `b` son el mismo elemento).
• Un preorden es una relación que es reflexiva y transitiva, pero no necesariamente simétrica.
• Una relación de congruencia es una relación de equivalencia que también "respeta" las operaciones de una estructura matemática (como la suma o la multiplicación).

Bien definido bajo una relación de equivalencia

Cuando una propiedad o una función se dice que está "bien definida" bajo una relación de equivalencia, significa que no importa qué elemento elijas de una clase de equivalencia, la propiedad o el resultado de la función será el mismo para todos los elementos de esa clase.

• Por ejemplo, si tienes la clase de los números pares, la propiedad "ser par" está bien definida, porque todos los elementos de esa clase son pares.

Galería de imágenes

• 

  Disquisitiones aritmeticae, obra de Gauss

• 

  Philip Jourdain, matemático y lógico británico

Véase también

En inglés: Equivalence relation Facts for Kids