Nucleosíntesis estelar para niños
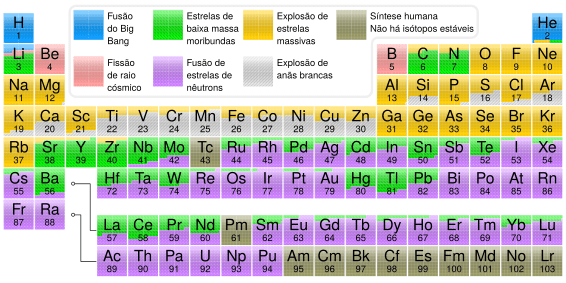
La nucleosíntesis estelar es el proceso en el que las estrellas crean los diferentes elementos químicos que existen en el universo. Esto ocurre a través de reacciones nucleares que transforman elementos más ligeros en otros más pesados. Algunos elementos, como el hidrógeno, el helio y el litio, se formaron al principio del universo, durante el Big Bang.
Este proceso es una parte clave de la evolución estelar. Cuando una estrella se queda sin el "combustible" para estas reacciones nucleares, su vida llega a su fin, lo que puede llevar a un colapso gravitatorio.
La teoría de la nucleosíntesis estelar nos ayuda a entender por qué los elementos químicos se encuentran en las cantidades que observamos en el universo. También explica cómo estas cantidades han cambiado con el tiempo. Esta idea fue propuesta por primera vez por Fred Hoyle en 1946. Más tarde, él y un equipo de científicos (Margaret y Geoffrey Burbidge, y William Alfred Fowler) escribieron un artículo muy importante en 1957, conocido como 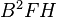 . Este trabajo explicó cómo se forman los elementos, incluyendo aquellos que se crean al capturar neutrones.
. Este trabajo explicó cómo se forman los elementos, incluyendo aquellos que se crean al capturar neutrones.
A principios del siglo XX, los científicos comenzaron a entender que solo las reacciones nucleares podían explicar por qué el Sol y otras estrellas brillan y dan calor durante tanto tiempo. Aproximadamente el 90% de la energía de las estrellas proviene de la fusión nuclear del hidrógeno para formar helio. Otro 6% de la energía viene de la fusión del helio para formar carbono. Las etapas de fusión de otros elementos contribuyen mucho menos a la energía total de una estrella.
Contenido
Historia de la nucleosíntesis estelar
Primeras ideas sobre la energía de las estrellas
En 1920, el científico Arthur Eddington sugirió por primera vez que las estrellas obtenían su energía al fusionar hidrógeno en helio. También pensó que las estrellas podrían crear elementos más pesados. Este fue un paso muy importante para entender cómo se forman los elementos en el universo.
En 1928, George Gamow desarrolló una fórmula matemática que explicaba cómo dos núcleos atómicos podían acercarse lo suficiente para fusionarse, a pesar de que se repelen entre sí. Esta fórmula ayudó a otros científicos, como Robert Atkinson y Fritz Houtermans, a calcular qué tan rápido ocurrían las reacciones nucleares dentro de las estrellas.
Descubrimientos clave sobre la fusión
En 1939, el científico Hans Bethe investigó cómo el hidrógeno se fusiona en helio. Propuso dos procesos principales:
- Las cadenas protón-protón: Son las reacciones más importantes en estrellas pequeñas, como nuestro Sol.
- El ciclo carbono-nitrógeno-oxígeno (ciclo CNO): Este ciclo es más importante en estrellas mucho más grandes. Fue descubierto también por Carl Friedrich von Weizsäcker en 1938.
Ambos procesos transforman cuatro protones en un núcleo de helio-4. Sin embargo, en ese momento no se explicó cómo se formaban los elementos más pesados.
La formación de elementos pesados
La idea de que las estrellas podían formar elementos más pesados vino de Fred Hoyle en 1946. Él sugirió que en el centro de las estrellas, donde hace mucho calor, se podían formar elementos como el hierro. En 1954, Hoyle publicó un trabajo explicando cómo las estrellas muy grandes podían crear elementos desde el carbón hasta el hierro en sus etapas avanzadas de fusión.
Más tarde, en 1957, el famoso artículo 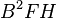 (escrito por Margaret Burbidge, Geoffrey Burbidge, Fowler y Hoyle) unió todas estas ideas. Este trabajo explicó de forma clara cómo se forman los diferentes elementos y cómo se crean los núcleos más pesados que el hierro, especialmente a través de la captura de neutrones.
(escrito por Margaret Burbidge, Geoffrey Burbidge, Fowler y Hoyle) unió todas estas ideas. Este trabajo explicó de forma clara cómo se forman los diferentes elementos y cómo se crean los núcleos más pesados que el hierro, especialmente a través de la captura de neutrones.
Otros científicos como Alastair G. W. Cameron y Donald D. Clayton también hicieron contribuciones importantes. Cameron usó computadoras para calcular cómo evolucionan los sistemas nucleares. Clayton, por su parte, calculó cómo se forman los elementos en procesos específicos de captura de neutrones y cómo se quema el silicio para formar el núcleo de hierro.
Reacciones importantes en las estrellas
Las reacciones más importantes que ocurren dentro de las estrellas para crear elementos son:
- Fusión del hidrógeno:
* La cadena protón-protón. * El ciclo CNO. * Fusión del deuterio.
- Fusión del helio:
* El proceso triple alfa. * El proceso alfa.
- Quema de metales (fusión de elementos más pesados):
* Proceso de combustión del carbono. * Proceso de combustión del oxígeno. * Proceso de combustión del neón. * Proceso de combustión del silicio.
- Producción de elementos más pesados que el hierro:
* Captura de neutrones: * El proceso s. * El proceso r. * Captura de protones: * proceso rp. * proceso p.
- Fotodesintegración.
Fusión del hidrógeno: el motor de las estrellas
La fusión del hidrógeno es el proceso principal que genera energía en el centro de las estrellas. En este proceso, cuatro protones se unen para formar un núcleo de helio-4. Esto no es como quemar algo con fuego, sino una reacción nuclear. Hay dos formas principales en que esto sucede: la cadena protón-protón y el ciclo CNO. La mayoría de las estrellas, excepto las enanas blancas, usan estos dos procesos.
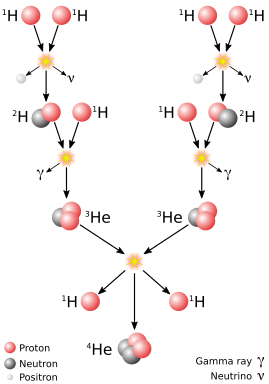
Cadena protón-protón
En estrellas más pequeñas, como nuestro Sol, la energía se produce principalmente por la cadena protón-protón. Aquí, dos protones se fusionan para formar un núcleo de deuterio (que tiene un protón y un neutrón). En este proceso se liberan pequeñas partículas como un positrón y un neutrino. Al final de todo el ciclo, se libera una gran cantidad de energía. Este proceso no cambia mucho su ritmo con pequeñas variaciones de temperatura.
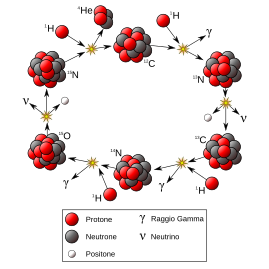
Ciclo CNO
En estrellas más grandes y masivas, el ciclo CNO es el que produce más energía. En este ciclo, el carbono, el nitrógeno y el oxígeno actúan como "ayudantes" para transformar el hidrógeno en helio. Al final del ciclo, también se libera mucha energía. A diferencia de la cadena protón-protón, el ciclo CNO es muy sensible a los cambios de temperatura. Un pequeño aumento de temperatura hace que produzca mucha más energía.
El Sol obtiene solo el 1% de su energía de este ciclo. La cadena protón-protón comienza a temperaturas más bajas, por lo que es el proceso principal en estrellas pequeñas. El ciclo CNO necesita temperaturas más altas para empezar, pero una vez que lo hace, se vuelve muy eficiente. Las estrellas que son 1.3 veces más grandes que el Sol usan principalmente el ciclo CNO.
Fusión del helio: el siguiente paso
Cuando las estrellas de la secuencia principal (como el Sol) fusionan hidrógeno, acumulan helio en sus núcleos. Pero el núcleo no está lo suficientemente caliente para fusionar el helio de inmediato. La fusión del helio comienza cuando la estrella se convierte en una gigante roja. En estrellas como el Sol, esto ocurre con un "flash de helio" en el núcleo. Luego, la estrella se mueve a una nueva etapa donde quema helio en su centro.
Las estrellas más grandes fusionan helio sin este "flash". Cuando el helio se agota en el núcleo, este se convierte principalmente en carbono y oxígeno. Las estrellas muy masivas se convierten en supergigantes y queman helio rápidamente.
El helio se fusiona en carbono a través del proceso triple-alfa. Esto significa que tres núcleos de helio se unen para formar carbono. Después, este carbono puede unirse con más helio para producir oxígeno, neón y otros elementos más pesados. Por eso, los procesos alfa suelen crear elementos con un número par de protones.
Quema de metales: creando elementos pesados
Si una estrella es lo suficientemente grande, después de agotar el helio, su núcleo se comprime y se calienta aún más. Esto permite que comience la fusión del carbono. En este punto, la estrella tendrá varias capas de fusión, como una cebolla: una capa de carbono, otra de helio y otra de hidrógeno.
Las estrellas muy masivas (más de 12 veces la masa del Sol) pueden pasar por todas las fases de fusión posibles hasta llegar al hierro. A medida que se fusionan elementos más pesados, las etapas duran menos tiempo. La etapa de gigante roja es la última transformación importante. Después de eso, la estrella se vuelve muy inestable antes de su destino final.
Fusión del carbono (estrellas grandes)
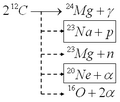
Cuando el helio se agota, el núcleo se comprime y se calienta a unos 500 millones de grados Celsius. A esta temperatura, los átomos de carbono comienzan a reaccionar entre sí, formando elementos más pesados. Esta etapa dura unos cientos de años. Las reacciones más comunes producen sodio-23 y neón-20. Al final, el núcleo estará compuesto principalmente de oxígeno-16, neón-20 y magnesio-24.
Fotodesintegración y fusión del neón
Después de que el carbono se agota, el núcleo se contrae y se calienta a 1.2 mil millones de grados Celsius. A estas temperaturas, los fotones (partículas de luz) son tan energéticos que pueden romper el neón-20. Aunque este proceso consume energía, sus subproductos dan lugar a otra reacción que sí la produce. Así, la estrella se mantiene mientras haya neón para fusionar. El resultado es más oxígeno y magnesio.
Fusión del oxígeno
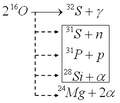
Cuando el neón se agota, el núcleo se calienta y se contrae de nuevo, alcanzando entre 1.5 y 2 mil millones de grados Celsius. A esta temperatura, el oxígeno comienza a fusionarse. Esta etapa dura solo unos pocos meses. Los elementos resultantes son principalmente silicio-28, azufre-34, calcio-42 y titanio-46.
Fotodesintegración y fusión del silicio
Finalmente, cuando el núcleo alcanza los 2.7 mil millones de grados Celsius, el silicio comienza a "quemarse" en una serie de reacciones complejas que solo sostendrán a la estrella por poco más de un día. Parte del silicio-28 se rompe por fotones muy energéticos, liberando protones, neutrones y partículas alfa que son capturadas por átomos más pesados. El silicio también se fusiona para formar níquel-56, que luego se transforma en hierro-56.
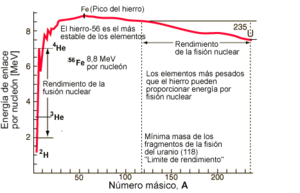
El hierro-56 es el elemento más estable. A partir de él, la fusión nuclear ya no produce energía, sino que la consume. En este punto, la estrella, que ya es muy inestable, no puede sostenerse más por sí misma.
Galería de imágenes
-
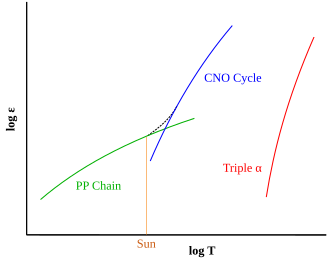
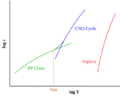
Energía relativa liberada (ε) en escala logarítmica en los procesos de fusión protón-protón (PP), CNO y triple-α para diferentes temperaturas (T). La línea negra muestra la generación de energía en procesos combinados PP y CNO en las estrellas. Para la temperatura del núcleo solar, el proceso más eficiente es el PP.
Véase también
 En inglés: Stellar nucleosynthesis Facts for Kids
En inglés: Stellar nucleosynthesis Facts for Kids