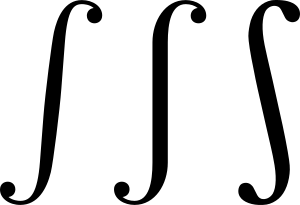Integración para niños

Enciclopedia para niños

La integración es una herramienta muy importante en las matemáticas, especialmente en el cálculo. Imagina que quieres calcular el área de una figura que no es un cuadrado o un círculo, sino que tiene bordes curvos. La integración te ayuda a hacer eso.

Básicamente, una integral es como una suma de muchísimos pedacitos muy, muy pequeños. Piensa en ella como una suma continua. Es la operación contraria a la derivada, que nos dice cómo cambia algo en un instante.

El cálculo integral es una parte de las matemáticas que se encarga de este proceso de integración. Se usa mucho en la ingeniería y en la ciencia. Sirve principalmente para calcular áreas de regiones y volúmenes de objetos con formas complejas.

Científicos como René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow fueron clave en el desarrollo de estas ideas. Newton y Leibniz, de forma independiente, descubrieron el teorema fundamental del cálculo. Este teorema nos dice que la derivación y la integración son operaciones inversas, como sumar y restar, o multiplicar y dividir.

¿Para qué sirve el cálculo integral?

El cálculo integral tiene muchos usos importantes. Algunos de sus objetivos principales son:

Calcular la velocidad y la distancia recorrida.
Encontrar el área de una región plana.
Calcular el volumen de un sólido de revolución (objetos que se forman al girar una figura plana).
Resolver problemas de integrales indefinidas e integrales definidas.
Entender cómo se relacionan la derivada y la integral a través del teorema fundamental del cálculo.

Entendiendo la integración

La integral de una función entre dos puntos se puede ver como el área bajo la curva de esa función.

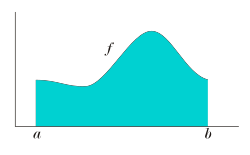
Imagina que tienes una función matemática $f(x)$ y quieres saber el área que hay debajo de su gráfica, entre dos puntos específicos, por ejemplo, $a$ y $b$ en el eje x. La integral de esa función en ese intervalo es precisamente esa área. Si la función está por debajo del eje x, el área se considera negativa.

El símbolo de la integral es una "S" alargada: 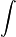$\int$ .

Los principios de la integración fueron establecidos por Isaac Newton y Gottfried Wilhelm Leibniz a finales del siglo XVII. Gracias al teorema fundamental del cálculo, que ellos desarrollaron, podemos calcular fácilmente una integral definida si conocemos una función cuya derivada sea la función original. Las integrales y las derivadas se convirtieron en herramientas esenciales del cálculo, con muchas aplicaciones en la ciencia y la ingeniería.

Más tarde, Bernhard Riemann dio una definición más precisa de la integral, basándose en la idea de aproximar el área dividiéndola en muchos rectángulos pequeños. A principios del siglo XIX, surgieron ideas más avanzadas, como la integral de Lebesgue, que permite integrar un rango más amplio de funciones.

Historia de la integración

Orígenes antiguos

La idea de la integración se remonta al antiguo Egipto, alrededor del 1800 a.C. El papiro de Moscú muestra que ya sabían cómo calcular el volumen de un tronco de pirámide.

La primera técnica sistemática para encontrar áreas y volúmenes fue el "método de exhausción" de Eudoxo de Cnido (alrededor del 370 a.C.). Este método consistía en dividir una figura en un número infinito de formas más simples cuyas áreas o volúmenes ya se conocían. Arquímedes lo usó para calcular el área de parábolas y aproximar el área de un círculo. En China, Liu Hui y Zu Chongzhi también usaron métodos similares para calcular el área de un círculo y el volumen de una esfera.

En el siglo XII, el matemático indio Bhaskara II también tuvo algunas ideas relacionadas con el cálculo integral.

Newton y Leibniz: El gran avance

Los avances más importantes en la integración ocurrieron en el siglo XVII con la formulación del teorema fundamental del cálculo, desarrollado de forma independiente por Isaac Newton y Gottfried Leibniz. Este teorema mostró la conexión entre la integración y la derivación. Esta conexión hizo que calcular integrales fuera mucho más fácil. El trabajo de Newton y Leibniz sentó las bases del cálculo moderno, y la notación que usamos hoy para las integrales viene directamente del trabajo de Leibniz.

La notación moderna

El símbolo de integral en escritos (de izquierda a derecha) ingleses, alemanes y rusos

Isaac Newton usaba símbolos diferentes para la integración, pero no fueron muy populares. La notación moderna de las integrales indefinidas fue introducida por Gottfried Leibniz en 1675. Él adaptó el símbolo "∫" de una letra "S" alargada, porque consideraba la integral como una suma infinita de partes muy pequeñas. La notación para las integrales definidas, con los límites arriba y abajo del signo, la usó por primera vez Joseph Fourier alrededor de 1819-20.

Existen pequeñas diferencias en cómo se dibuja el símbolo de la integral en diferentes idiomas. Por ejemplo, en inglés se inclina a la derecha, mientras que en alemán se escribe recto.

Conceptos y aplicaciones prácticas

Aproximaciones a la integral de

\sqrt{x}

entre 0 y 1, con ■ 5 muestras por la izquierda (arriba) y ■ 12 muestras por la derecha (abajo).

Las integrales aparecen en muchas situaciones de la vida real. Imagina que quieres saber cuánta agua cabe en una piscina con una forma irregular y un fondo curvo. Con la integración, puedes calcular su volumen exacto.

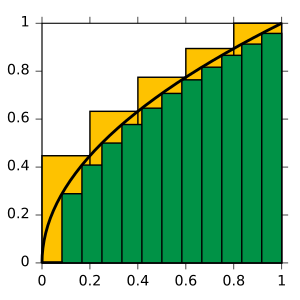
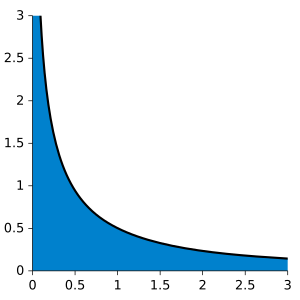
Para entender cómo se calcula el área bajo una curva, veamos un ejemplo. Considera la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y=f(x)=\sqrt{x} entre 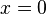$x=0$ y $x=1$ . Queremos saber el área bajo esta curva. La notación para esta integral es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \int_0^1 \sqrt x \, \text{d}x .

Una forma de aproximar esta área es dividirla en pequeños rectángulos. Si dividimos el intervalo en cinco partes y sumamos las áreas de los rectángulos, obtenemos una aproximación. Cuantos más rectángulos pequeños usemos, más precisa será nuestra aproximación. La idea clave de la integral es que usamos "pasos infinitamente finos" o "infinitesimales" para obtener el valor exacto.

El teorema fundamental del cálculo nos permite calcular estas integrales de forma precisa. Para la función 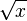$\sqrt{x}$ , la función relacionada (llamada primitiva) es 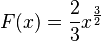$F(x)=\frac 2 3 x^\frac 3 2$ . Para encontrar el área exacta, solo tenemos que calcular Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F(1)-F(0) , lo que nos da Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac 2 3 .

Propiedades de la integración

Linealidad

La integración es una operación "lineal". Esto significa dos cosas:

Si sumas dos funciones y luego las integras, el resultado es el mismo que si integras cada función por separado y luego sumas los resultados.
Si multiplicas una función por un número y luego la integras, el resultado es el mismo que si integras la función y luego multiplicas el resultado por ese número.

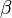En símbolos, esto se ve así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \int_a^b (\alpha f + \beta g)(x) \, \text{d}x = \alpha \int_a^b f(x) \,\text{d}x + \beta \int_a^b g(x) \, \text{d}x. \, Donde $\alpha$ y $\beta$ son números.

Desigualdades

Las integrales también cumplen con algunas desigualdades importantes:

Límites: Si una función está entre dos valores (m y M) en un intervalo, su integral también estará entre el área mínima (m por el ancho del intervalo) y el área máxima (M por el ancho del intervalo).
Comparación de funciones: Si una función es siempre menor o igual que otra en un intervalo, su integral también será menor o igual que la integral de la otra función.
Subintervalos: Si integras una función no negativa en un subintervalo, el resultado será menor o igual que si la integras en el intervalo completo.
Valores absolutos: La integral del valor absoluto de una función es siempre mayor o igual que el valor absoluto de la integral de la función.

Teorema fundamental del cálculo

Las operaciones de integración y diferenciación son inversas entre sí (animación usando una función lineal como ejemplo)

El teorema fundamental del cálculo es una de las ideas más importantes en matemáticas. Nos dice que la derivación y la integración son operaciones inversas. Si integras una función y luego la derivas, obtienes la función original.

Una consecuencia muy útil de este teorema es que nos permite calcular integrales definidas usando una "primitiva" de la función. Una primitiva es una función cuya derivada es la función original.

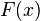En resumen, si tienes una función $f(x)$ y encuentras su primitiva $F(x)$ , entonces la integral de $f(x)$ desde $a$ hasta $b$ es simplemente Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F(b) - F(a) . Esto simplifica mucho los cálculos.

Extensiones de la integración

Integrales impropias

La integral impropia
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \int_{0}^{\infty} \frac{\text{d}x}{(x+1)\sqrt{x}} = \pi
tiene intervalos no acotados tanto en el dominio como en el recorrido.

A veces, queremos integrar funciones en intervalos que no están acotados (por ejemplo, hasta el infinito) o funciones que se vuelven infinitas en algún punto. Estas son las "integrales impropias". Para resolverlas, usamos el concepto de límite. Calculamos la integral en un intervalo finito y luego vemos qué pasa cuando los límites de ese intervalo se acercan al infinito o al punto donde la función se vuelve infinita.

Por ejemplo, la integral de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{(x+1)\sqrt{x}} desde 0 hasta infinito es una integral impropia. Se puede calcular dividiéndola en dos partes y tomando límites, y el resultado es $\pi$ .

Integración múltiple

Integral doble como el volumen limitado por una superficie

Las integrales no solo se usan para áreas en un plano. También se pueden usar para calcular volúmenes en tres dimensiones o incluso "hipervolúmenes" en dimensiones superiores. Esto se llama "integración múltiple".

Una integral doble de una función de dos variables puede representar el volumen entre la superficie de la función y el plano xy. Una integral triple puede calcular el volumen de un objeto tridimensional.

Por ejemplo, el volumen de una caja de 4x6x5 se puede calcular con una integral doble de la función constante 5 sobre la base de la caja, o con una integral triple de la función constante 1 sobre toda la caja.

Integrales de línea y superficie

Una integral de línea acumula elementos a lo largo de una curva

La definición de las integrales de superficie descansa en la división de la superficie en pequeños elementos de superficie.

El concepto de integral se puede extender a caminos curvos (integrales de línea) y a superficies (integrales de superficie). Estas son muy importantes en la física, especialmente cuando se trabaja con campos vectoriales.

Una integral de línea calcula la suma de los valores de una función a lo largo de una curva. Por ejemplo, se usa para calcular el trabajo realizado por una fuerza al mover un objeto a lo largo de un camino curvo.

Una integral de superficie calcula la suma de los valores de una función sobre una superficie. Se usa, por ejemplo, para calcular el caudal de un fluido que atraviesa una superficie, o el flujo eléctrico o magnético a través de ella.

Métodos para calcular integrales

Cálculo de integrales paso a paso

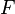La forma más común de calcular una integral de una variable real es usando el teorema fundamental del cálculo: 1. Elige una función $f(x)$ y un intervalo $[a,b]$ . 2. Encuentra una primitiva de $f$ , es decir, una función $F$ tal que su derivada 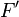$F'$ sea igual a $f$ . 3. Aplica el teorema: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \int_a^b f(x)\,\text{d}x = F(b)-F(a). 4. El resultado es el valor de la integral.

Encontrar la primitiva de $f$ puede ser la parte más difícil. Para ello, existen muchas técnicas, como:

Integración por cambio de variable
Integración por partes
Integración por sustitución trigonométrica
Integración de fracciones parciales

A veces, incluso con estas técnicas, no es posible encontrar una fórmula exacta para la primitiva.

Cuadratura numérica

Métodos numéricos de cuadratura: ■ Rectángulo, ■ Trapezoide, ■ Romberg, ■ Gauss

Muchas integrales que aparecen en problemas reales no se pueden calcular de forma exacta o son muy complicadas. Por eso, se usan métodos numéricos para aproximar las integrales. Estos métodos son muy importantes en los ordenadores.

El objetivo de la integración numérica es obtener una aproximación lo más exacta y confiable posible. Estos métodos dividen el intervalo de integración en muchos trozos pequeños y usan fórmulas para estimar el área o volumen.

Algunas aplicaciones de la integración

Valor medio de una función

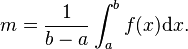Para calcular el valor medio de una función $f$ en un intervalo $[a,b]$ , se usa la fórmula: $m=\frac{1}{b-a}\int_a^b f(x) \mathrm{d}x.$ Esto es como una extensión de la media aritmética para funciones continuas.

Aplicaciones en física

Muchas leyes de la Física se expresan con ecuaciones que se resuelven usando integrales.

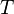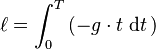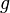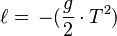Por ejemplo, si un objeto cae libremente, su velocidad aumenta debido a la gravedad. Para saber la distancia que ha recorrido en un tiempo $T$ , se puede usar una integral: $\ell = \int_0^T \left(-g \cdot t\;\mathrm{d}t\,\right)$ Donde $g$ es la aceleración de la gravedad. El resultado es $\ell =\, -(\frac g 2 \cdot T^2)$ .

Otros ejemplos de aplicaciones en física:

La energía consumida en un tiempo es la integral de la potencia durante ese tiempo.
La variación de la carga eléctrica en un condensador es la integral de la corriente eléctrica que fluye hacia él.
La integración del caudal de un fluido en un conducto nos da el volumen total de fluido que ha pasado.

Véase también

En inglés: Integral Facts for Kids

Tabla de integrales
Integración numérica
Derivada
Signo de Integral
Sumatorio
Límite matemático
Infinito
Integral de línea
Cambio de variable
Integrales definidas
Integrales indefinidas

Obtenido de «https://ninos.kiddle.co/index.php?title=Integración&oldid=4717171»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Integración para Niños. Enciclopedia Kiddle.