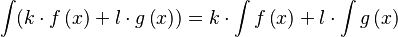Integración indefinida para niños
En el mundo de las matemáticas, especialmente en una rama llamada cálculo infinitesimal, la función primitiva o antiderivada de una función f es como encontrar el "origen" de esa función. Imagina que tienes una función f que es el resultado de "derivar" otra función. La función primitiva F es esa función original, de la cual f es la derivada. Es decir, si derivas F, obtienes f.
Para que una función f tenga primitivas en un intervalo (un rango de números), debe ser continua en ese intervalo. Esto significa que su gráfica no tiene saltos ni interrupciones.
Si una función f tiene una primitiva, en realidad tiene muchísimas. Todas estas primitivas son muy parecidas: solo se diferencian por un número constante. Por ejemplo, si F1 y F2 son dos primitivas de f, siempre habrá un número C tal que F1 = F2 + C. A este número C se le llama la constante de integración.
Así, si F es una primitiva de f, el conjunto de todas sus primitivas se escribe como F + C. A este conjunto se le conoce como integral indefinida de f y se representa con un símbolo especial:
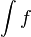 o también
o también 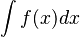
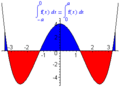
El proceso de encontrar la primitiva de una función se llama integración indefinida. Es el proceso inverso a la derivación. Las integrales indefinidas están conectadas con las integrales definidas a través de un concepto muy importante llamado teorema fundamental del cálculo. Esto nos ayuda a calcular áreas y otras cosas de manera más sencilla.
Contenido
Ejemplo de función primitiva
Vamos a ver un ejemplo. Si tenemos la función 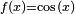 (el coseno de x), una de sus primitivas es la función
(el coseno de x), una de sus primitivas es la función  (el seno de x). ¿Por qué? Porque si derivamos
(el seno de x). ¿Por qué? Porque si derivamos 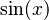 , obtenemos
, obtenemos 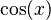 .
.
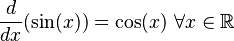
Como la derivada de cualquier número constante es cero, la función 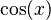 tendrá infinitas primitivas. Por ejemplo,
tendrá infinitas primitivas. Por ejemplo, 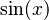 , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin(x) + 5 , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin(x) - 100 , y así sucesivamente. Todas ellas son primitivas de
, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin(x) + 5 , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin(x) - 100 , y así sucesivamente. Todas ellas son primitivas de 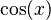 . En general, cualquier primitiva de
. En general, cualquier primitiva de 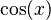 se puede escribir como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin(x) + C , donde C es la constante de integración.
se puede escribir como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin(x) + C , donde C es la constante de integración.
¿Qué es la constante de integración?
La constante de integración aparece porque la derivada de cualquier función constante (un número fijo) es siempre cero. Cuando encontramos una primitiva F, si le sumamos o restamos cualquier número C, obtenemos otra primitiva válida. Esto es porque al derivar F + C, obtenemos la derivada de F más la derivada de C (que es cero). Así, (F + C)' = F ' + 0 = F '.
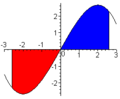
Esta constante nos dice que hay muchas funciones que tienen la misma derivada. Imagina que la función f(x) nos da la pendiente de otra función F(x) en cada punto. Si dibujamos en cada punto (x, y) del plano cartesiano un pequeño segmento con la pendiente f(x), obtenemos un "campo de direcciones" como el que se ve en la imagen.
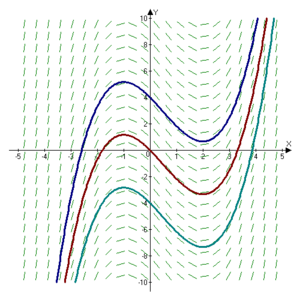
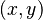 del plano donde
del plano donde 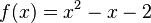 . Se muestran tres curvas de las infinitas posibles curvas primitivas de
. Se muestran tres curvas de las infinitas posibles curvas primitivas de  que se pueden obtener variando la constante de integración.
que se pueden obtener variando la constante de integración.El problema de encontrar una función F(x) cuya derivada sea f(x) es como encontrar una curva que siempre siga la dirección de esos pequeños segmentos. Como puedes ver en la imagen, al cambiar la constante de integración C, obtenemos diferentes curvas que cumplen esta condición. Estas curvas son simplemente traslaciones verticales (movimientos hacia arriba o hacia abajo) unas de otras.
Propiedades de la integral indefinida
Linealidad de la integral indefinida
La integración indefinida es "lineal". Esto significa dos cosas importantes:
- Si F es una primitiva de una función f, entonces si multiplicamos f por un número k, la primitiva de k veces f será k veces F.
- Si F y G son primitivas de dos funciones f y g respectivamente, entonces la primitiva de la suma de f y g es la suma de sus primitivas, F + G.
Esto se puede escribir de forma matemática así:
Cómo calcular primitivas
Integrales inmediatas
Para encontrar la primitiva de una función, a menudo podemos "descomponerla" en partes más simples. Estas partes son funciones básicas cuyas primitivas ya conocemos o podemos encontrar fácilmente mirando una tabla de derivadas "al revés". Luego, aplicamos la propiedad de linealidad que acabamos de ver.
Aquí tienes una tabla con algunas de las funciones más comunes y sus primitivas:
Función 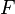 : primitiva de : primitiva de 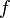 |
función 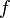 : derivada de : derivada de 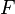 |
|---|---|
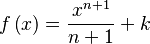 |
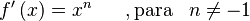 |
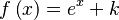 |
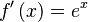 |
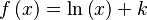 |
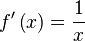 |
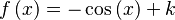 |
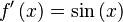 |
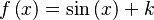 |
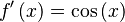 |
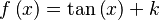 |
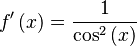 |
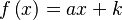 |
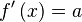 |
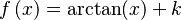 |
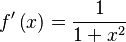 |
Por ejemplo, si queremos encontrar una primitiva de la función x → x(2-3x). Primero, desarrollamos la expresión: x(2-3x) = 2x - 3x2. Sabemos que 2x es la derivada de x2, y 3x2 es la derivada de x3. Entonces, la primitiva de 2x - 3x2 es x2 - x3 + k.
Si nos piden que la primitiva cumpla una condición específica, como que F(2) = 3, entonces podemos encontrar el valor exacto de k. En el ejemplo anterior, si F(2) = 3, entonces 22 - 23 + k = 3. Esto es 4 - 8 + k = 3, lo que significa -4 + k = 3. Por lo tanto, k debe ser 7.
Métodos de integración
Existen varios métodos para calcular primitivas, especialmente cuando las funciones son más complejas:
- La linealidad de la integración nos ayuda a dividir problemas grandes en otros más pequeños.
- La Integración por sustitución es útil para simplificar la función antes de integrar.
- La Integración por partes se usa para integrar productos de funciones.
- El método de fracciones parciales nos permite integrar funciones que son fracciones de dos polinomios.
- También se pueden usar tablas de integrales ya calculadas.
Galería de imágenes
Véase también
- Integración
- Integral definida
- Integración simbólica
- Anexo:Integrales