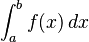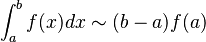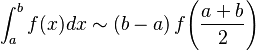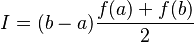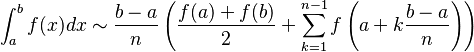Integración numérica para niños
En el análisis numérico, que es una rama de las matemáticas que usa números para resolver problemas, la integración numérica es un conjunto de métodos. Estos métodos nos ayudan a calcular el valor aproximado de una integral definida. Una integral definida es como encontrar el área bajo una curva en un gráfico, entre dos puntos específicos. A veces, este término también se usa para describir cómo resolver ecuaciones diferenciales con números.
El término cuadratura numérica es muy parecido a integración numérica. Se usa especialmente cuando calculamos el área de una sola dimensión. Sin embargo, también se puede usar para áreas en dos o más dimensiones, como las integrales múltiples.
El objetivo principal de la integración numérica es encontrar una solución aproximada para una integral definida, que se ve así:
Este problema también se puede ver como un problema de valor inicial para una ecuación diferencial ordinaria. Es como si tuviéramos una función que nos dice cómo algo cambia, y queremos saber su valor final.
Contenido
¿Por qué usamos la integración numérica?
Hay varias razones importantes por las que necesitamos la integración numérica:
¿Cuándo es difícil calcular una integral?
A veces, calcular una integral de forma exacta es muy complicado o incluso imposible. Algunas funciones son tan complejas que no hay una fórmula sencilla para su integral. En estos casos, los métodos numéricos nos ofrecen una manera más fácil de encontrar una respuesta.
Soluciones aproximadas pero muy precisas
Una solución exacta de una integral nos daría un valor perfecto. Sin embargo, la integración numérica nos da una solución aproximada. La buena noticia es que el error de esta aproximación puede ser tan pequeño que el resultado numérico es casi idéntico al exacto, al menos en las primeras cifras decimales. La precisión depende del método que usemos.
Métodos para integrales de una dimensión
Los métodos de integración numérica suelen combinar varias evaluaciones de la función para obtener una aproximación del área. Es importante analizar cuánto error produce cada método y cuántas veces necesita evaluar la función. Un método es mejor si da un error pequeño con pocas evaluaciones.
Reducir el número de veces que evaluamos la función ayuda a que los cálculos sean más rápidos. También disminuye el error de redondeo, que son pequeños errores que ocurren cuando las computadoras trabajan con números muy largos y tienen que redondearlos.
Cuando usamos estos métodos, no sabemos el valor exacto del error. Por eso, los métodos trabajan con estimaciones del error o con límites máximos para el error.
Métodos basados en funciones de interpolación
Muchos métodos de integración numérica funcionan aproximando la función original 
con otra función más sencilla, 
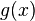, cuya integral sí conocemos. Esta función 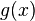se elige de manera que pase por algunos puntos de la función original. A esto se le llama interpolación. Generalmente, estas funciones sencillas son polinomios.
Fórmulas de Newton-Cotes
Las fórmulas de Newton-Cotes se obtienen cuando usamos polinomios para interpolar la función, y los puntos donde evaluamos están igualmente espaciados. Algunos ejemplos famosos son la regla del rectángulo, la regla del trapecio y la regla de Simpson.
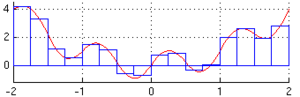
Regla del rectángulo
Este es el método más sencillo. Imagina que el área bajo la curva se divide en muchos rectángulos pequeños. La altura de cada rectángulo se toma del valor de la función en un punto.
Regla del punto medio
Similar a la regla del rectángulo, pero la altura del rectángulo se toma del valor de la función justo en el punto medio del intervalo.
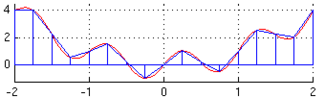
Regla del trapecio
En lugar de rectángulos, este método usa trapecios para aproximar el área. La parte superior de cada trapecio conecta dos puntos de la función con una línea recta.
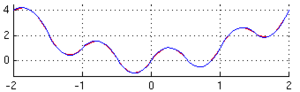
Regla de Simpson
Este método es más preciso porque usa un polinomio de segundo grado (una parábola) para aproximar la función. Necesita evaluar la función en tres puntos: los dos extremos del intervalo y el punto medio.
![\int_{a}^{b} f(x) \, dx \approx \frac{b-a}{6}\left[f(a) + 4f\left(\frac{a+b}{2}\right)+f(b)\right]](/images/math/8/0/c/80ca47af148fedc25f9b42d84725c0b2.png)
.
Reglas compuestas
Para obtener una aproximación aún más precisa, podemos dividir el intervalo total en muchos subintervalos más pequeños. Luego, aplicamos una de las reglas (como la del trapecio o Simpson) a cada subintervalo y sumamos todos los resultados. Estas se llaman reglas compuestas. Por ejemplo, la regla del trapecio compuesta se ve así:
Donde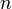 
es el número de subintervalos.
Algoritmos adaptativos
A veces, la función que queremos integrar cambia mucho en algunas partes y poco en otras. Los algoritmos adaptativos son inteligentes: usan pasos más pequeños (más divisiones) donde la función cambia mucho para ser más precisos, y pasos más grandes donde la función es más suave para ahorrar tiempo.
Integrales múltiples
Los métodos que hemos visto hasta ahora son para calcular áreas en una sola dimensión. Pero, ¿qué pasa si queremos calcular volúmenes o áreas en más dimensiones?
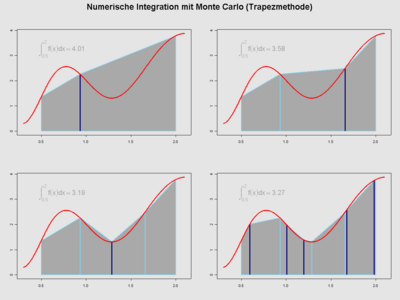
Montecarlo
Los métodos de Montecarlo son muy útiles para integrales de muchas dimensiones. En lugar de dividir el espacio en una cuadrícula, estos métodos eligen puntos al azar dentro del área o volumen que queremos calcular. Luego, usan esos puntos para estimar el valor de la integral. Son muy buenos porque su precisión no disminuye tanto cuando el número de dimensiones aumenta, a diferencia de otros métodos.
Conexión con las ecuaciones diferenciales
Calcular una integral definida también se puede relacionar con resolver un tipo de ecuación diferencial ordinaria. Si pensamos en la integral como una función que nos dice cuánto se ha acumulado algo hasta cierto punto, entonces la velocidad a la que se acumula es la función original. Los métodos que se usan para resolver ecuaciones diferenciales también pueden servir para calcular integrales.
Programas para integración numérica
La integración numérica es un campo muy estudiado en las matemáticas aplicadas. Hay muchos programas y bibliotecas de software que ya tienen implementados estos algoritmos para que los científicos e ingenieros puedan usarlos fácilmente.
Puedes encontrar algoritmos de integración numérica en GAMS class H2.
Véase también
En inglés: Numerical integration Facts for Kids
