Física matemática para niños
La matemática de la física (o física matemática) es un campo de estudio que explora la conexión entre la física y las matemáticas. Se trata de usar las matemáticas para resolver problemas de física y, a la vez, desarrollar nuevas herramientas matemáticas que ayuden a entender mejor el universo. Por ejemplo, se aplica en temas como la teoría de la elasticidad (cómo se deforman los materiales), la acústica (el sonido), la termodinámica (el calor), la electricidad, el magnetismo y la aerodinámica (el movimiento del aire).
Contenido
¿Cómo se conectan la Física y las Matemáticas?
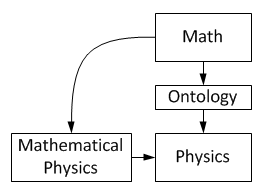
La física y las matemáticas están muy unidas. A menudo, los descubrimientos en física necesitan nuevas formas de matemáticas, y estas nuevas matemáticas luego ayudan a entender mejor el mundo físico.
La Relatividad y las Matemáticas
Las famosas teorías de la relatividad especial y la relatividad general de Albert Einstein necesitaron un tipo especial de matemáticas. La teoría de grupos fue muy importante al principio. Luego, la geometría diferencial y la topología se volvieron esenciales para describir fenómenos del universo, como los agujeros negros o la forma del espacio.
Estas teorías influyeron mucho en el desarrollo de:
- La geometría diferencial, especialmente la geometría de Riemann.
- La topología diferencial.
- La teoría de grupos.
La Mecánica Cuántica y las Matemáticas
La mecánica cuántica estudia el comportamiento de las partículas más pequeñas del universo. Para entenderla, se desarrollaron al mismo tiempo campos de las matemáticas como el álgebra lineal y el análisis funcional. Estas matemáticas son la base de esta parte de la física.
El concepto de "espectro" en matemáticas, que se refiere a los posibles valores de un operador, viene de la física. Se usaba para describir los colores de la luz que emiten los átomos (los espectros atómicos).
Varias áreas de las matemáticas fueron muy influenciadas por la mecánica cuántica:
- La teoría de los espacios de Hilbert (que son espacios matemáticos muy grandes).
- La teoría espectral.
- La teoría de representación de grupos (cómo los grupos matemáticos pueden representarse con transformaciones).
El Caos y los Sistemas Dinámicos
La teoría del caos estudia sistemas que son muy sensibles a pequeños cambios, como el clima. A menudo se describe usando sistemas dinámicos, que son modelos matemáticos que muestran cómo algo cambia con el tiempo. Esto llevó al desarrollo de la teoría de las ecuaciones diferenciales y algunas áreas de la topología diferencial.
Incluso algunas ideas de la topología (el estudio de las formas y los espacios) fueron inspiradas por problemas de física. Por ejemplo, las ideas de Henri Poincaré sobre cómo se comportan ciertos sistemas están muy relacionadas con la física.
La Probabilidad y la Mecánica Estadística
La mecánica estadística es un campo que usa la teoría de probabilidades para entender cómo se comportan grandes grupos de partículas. Está muy relacionada con la teoría ergódica, que estudia el comportamiento promedio de los sistemas a lo largo del tiempo.
El concepto de entropía (una medida del desorden) en la teoría de la información viene de la física. Ludwig Boltzmann la relacionó con las probabilidades de los estados de las partículas.
También hay una conexión creciente entre la combinatoria (el estudio de cómo contar y organizar cosas) y la física, especialmente en la física estadística.
Un Poco de Historia
A lo largo de la historia, muchos avances en matemáticas surgieron por la necesidad de resolver problemas de física.
- Por ejemplo, el cálculo diferencial y las ecuaciones diferenciales se hicieron muy importantes después de que Isaac Newton los usara para formular sus famosas leyes de Newton sobre el movimiento.
- El cálculo variacional (que busca la mejor forma de hacer algo) comenzó al intentar resolver problemas físicos, como encontrar la curva más rápida para que un objeto se deslice (el problema de la braquistócrona).
La geometría de Riemann, creada por Bernhard Riemann, se volvió muy relevante cuando Albert Einstein la usó en su teoría general de la relatividad. De hecho, conceptos como el tensor de curvatura de Riemann son clave en las ecuaciones de la relatividad.
Aunque David Hilbert ya había introducido la idea de espacio de Hilbert, muchos problemas relacionados con estos espacios se resolvieron con el desarrollo de la mecánica cuántica. En 1926, John von Neumann usó los espacios de Hilbert para describir la mecánica cuántica de forma matemática.
Más recientemente, algunos físicos han relacionado la existencia de diferentes tipos de partículas con conceptos matemáticos como los grupos de homología de las variedades de Calabi-Yau. A veces, los físicos intuyen soluciones a problemas complejos que luego son demostradas rigurosamente por los matemáticos.
Véase también
 En inglés: Mathematical physics Facts for Kids
En inglés: Mathematical physics Facts for Kids