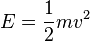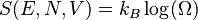Mecánica estadística para niños
La mecánica estadística es una rama de la física que usa las probabilidades para entender cómo se comportan los sistemas físicos muy grandes. Imagina un vaso de agua: tiene muchísimas moléculas. La mecánica estadística nos ayuda a predecir cómo se comportará ese vaso de agua (su temperatura, presión, etc.) basándose en cómo se mueven y chocan sus moléculas, sin tener que seguir a cada una por separado.
Los sistemas "macroscópicos" son aquellos que podemos ver y tocar, como un vaso de agua o el aire en una habitación. Estos sistemas están formados por una cantidad enorme de partículas, como átomos o moléculas. ¡Estamos hablando de números tan grandes como un 1 seguido de 23 ceros! Es imposible seguir el movimiento de cada una de estas partículas, incluso con las computadoras más potentes.
La mecánica estadística es muy útil porque conecta el comportamiento de las partículas más pequeñas (el mundo "microscópico") con el comportamiento general que observamos (el mundo "macroscópico"). Así, si entendemos cómo se mueven las partículas, podemos saber cómo se comportará el sistema en su conjunto. Esta rama de la física nos ayuda a describir muchos fenómenos, como los procesos en biología o química.
La mecánica estadística nació del estudio de la termodinámica, que es la ciencia que estudia el calor y la energía. La termodinámica ya explicaba propiedades como la temperatura y la presión de los sistemas grandes. La mecánica estadística fue un paso más allá, explicando estas propiedades a partir del movimiento de las partículas individuales.
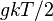(siendo g el número de grados de libertad, k la constante de Boltzmann y T la temperatura absoluta.Contenido
¿Cómo se aplica la Mecánica Estadística?
Un buen ejemplo de aplicación es el estudio de los gases. La termodinámica ya había descubierto leyes que describen cómo se comportan los gases, como la ley de Boyle-Mariotte o la ecuación del gas ideal. Gracias a la mecánica estadística, podemos entender por qué estas leyes funcionan.
Entendiendo el comportamiento de los gases
La mecánica estadística nos permite deducir las leyes de los gases asumiendo que sus partículas se mueven libremente y chocan entre sí y con las paredes del recipiente. La energía cinética de una partícula (su energía de movimiento) se calcula con la fórmula:
donde m es la masa y v es la velocidad.
El comportamiento general de un gas, como su presión, volumen y temperatura, depende de estas pocas variables macroscópicas. Este enfoque para estudiar los gases se conoce como teoría cinética.
¿Por qué es diferente de otras ramas de la física?
- La mecánica clásica intentaría calcular el camino exacto de cada partícula en un gas, lo cual es imposible por la cantidad de ellas.
- La termodinámica estudia las propiedades generales del gas sin preocuparse por lo que hacen las partículas individuales.
- La mecánica estadística es un punto intermedio. No sigue a cada partícula, sino que se enfoca en los promedios de su comportamiento. Así, podemos entender las propiedades de un gas a partir de lo que sabemos de sus moléculas, usando las leyes de la mecánica.
Historia de la Mecánica Estadística
Los primeros pasos de la mecánica estadística se dieron en el siglo XVIII, cuando Daniel Bernoulli usó ideas de probabilidad para explicar cómo se comportan los fluidos.
A mediados del siglo XIX, la termodinámica ya era una parte establecida de la física. Al mismo tiempo, la teoría cinética de los gases, que explicaba los gases a partir del movimiento de sus partículas, empezó a desarrollarse.
Un momento clave fue en 1872, cuando Ludwig Boltzmann estableció una conexión directa entre la entropía (una medida del desorden o la energía no utilizable en un sistema) y el movimiento de las moléculas.
Los principales fundadores de la mecánica estadística son:
- Ludwig Boltzmann: Explicó la entropía en términos de las diferentes formas en que las partículas pueden organizarse.
- James Clerk Maxwell: Desarrolló modelos de probabilidad para describir cómo se distribuyen las velocidades de las partículas.
- Josiah Willard Gibbs: Acuñó el nombre de "mecánica estadística" en 1884.
En 1859, James Clerk Maxwell formuló la Distribución de Maxwell-Boltzmann, que describe la proporción de moléculas que tienen una velocidad específica en un gas. Esta fue la primera ley estadística en la física. Cinco años después, Ludwig Boltzmann continuó desarrollando estas ideas.
El trabajo de Boltzmann en la década de 1870 fue fundamental. Introdujo el concepto de "conjunto estadístico" para describir sistemas en equilibrio y también investigó sistemas que no estaban en equilibrio.
El término "mecánica estadística" fue creado por Josiah Willard Gibbs en 1884. Gibbs publicó en 1902 el libro Principios elementales de mecánica estadística, que formalizó esta rama de la física. Sus métodos eran tan generales que se adaptaron fácilmente a la mecánica cuántica que surgió después, y siguen siendo la base de la mecánica estadística hoy en día.
Aplicación en otros campos
Aunque la mecánica estadística se basa en las leyes de la mecánica clásica o la mecánica cuántica, sus técnicas pueden usarse en otras áreas. Por ejemplo, se ha utilizado para entender la distribución de ingresos en economía, un campo llamado econofísica.
Relación entre Estadística y Termodinámica
La conexión entre los estados microscópicos (las partículas) y los estados macroscópicos (lo que observamos) se describe con la famosa fórmula de Ludwig Boltzmann para la entropía:
Aquí, S es la entropía, 
es el número de formas diferentes en que las partículas pueden organizarse para una energía, volumen y número de partículas dados, y 
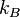es la constante de Boltzmann.
Esta fórmula muestra cómo la entropía de un sistema (una propiedad macroscópica) está relacionada con el número de posibles arreglos de sus partículas (una propiedad microscópica). Aunque esta relación fue propuesta por Boltzmann, no fue aceptada de inmediato por todos los científicos de su época.
La entropía como medida del desorden
En muchos libros de termodinámica, la entropía se explica como una medida del desorden de un sistema. De hecho, a veces se dice que "el desorden de un sistema aislado solo aumenta".
Es importante saber que esta idea de la entropía como desorden viene de la mecánica estadística. La termodinámica por sí sola no puede establecer esta relación porque no se ocupa de los estados microscópicos. La mecánica estadística, al partir de principios más básicos (los de la mecánica), puede "demostrar" el segundo principio de la termodinámica, que habla del aumento del desorden. Esta fue una gran contribución de Ludwig Boltzmann.
Formas de calcular en Mecánica Estadística
La mecánica estadística moderna describe un sistema físico usando "colectividades", que son conjuntos de todas las configuraciones posibles de las partículas y las probabilidades de cada una.
A cada colectividad se le asocia una "función de partición". Con esta función, se pueden calcular las propiedades termodinámicas del sistema. Dependiendo de cómo el sistema interactúa con su entorno, hay tres tipos principales de colectividades:
- La colectividad microcanónica: Describe un sistema completamente aislado, que no intercambia energía ni partículas con el exterior. Su energía es constante.
- La colectividad canónica: Describe un sistema que está en equilibrio de temperatura con un entorno más grande. Solo puede intercambiar energía en forma de calor.
- La colectividad gran canónica: Se usa para sistemas abiertos que pueden intercambiar tanto energía como partículas con el exterior.
Véase también
En inglés: Statistical mechanics Facts for Kids
- Ludwig Boltzmann
- Entropía
- Termodinámica
- Sistema de partículas
