Demostración matemática para niños
En matemáticas, una demostración o prueba es una forma de mostrar que una idea o afirmación matemática es verdadera. Para hacerlo, se usan otras ideas que ya sabemos que son ciertas, como teoremas (que son afirmaciones ya probadas) o axiomas (que son ideas básicas que se aceptan como verdaderas sin necesidad de prueba).
Las demostraciones son un tipo de razonamiento deductivo. Esto significa que, si las ideas iniciales son verdaderas, la conclusión de la demostración también debe serlo. A diferencia de las ideas que se basan en la experiencia o en ejemplos (razonamiento inductivo), una demostración matemática debe mostrar que una afirmación es siempre verdadera, sin excepción. Si una afirmación se cree que es verdadera pero aún no se ha demostrado, se le llama conjetura.
Las demostraciones usan la lógica y a menudo se escriben con lenguaje natural, aunque a veces pueden ser un poco ambiguas. Las demostraciones muy precisas, escritas con símbolos especiales, se estudian en un área llamada teoría de la demostración.
Si no conocemos una demostración para una afirmación, eso no significa que sea falsa. Solo si demostramos que su opuesto es verdadero, entonces la afirmación original sería falsa.
Contenido
¿De dónde viene la palabra "prueba"?
La palabra "prueba" viene del latín probare, que significa 'probar' o 'comprobar'. De ahí vienen otras palabras como "probar" (degustar o ensayar) y "probabilidad".
Un poco de historia de las demostraciones
Antes de que existieran las demostraciones matemáticas estrictas, la gente usaba dibujos o comparaciones para explicar ideas. La idea de demostrar una conclusión surgió probablemente con la geometría, que al principio significaba "medir la tierra".
El desarrollo de las demostraciones matemáticas es uno de los mayores logros de la matemática Griega antigua.
- Tales de Mileto (hace mucho tiempo, alrededor del 600 a.C.) demostró algunos teoremas de geometría.
- Más tarde, matemáticos como Eudoxo de Cnido y Teeteto formularon teoremas, pero no siempre los demostraron.
- Aristóteles (alrededor del 300 a.C.) dijo que las definiciones debían explicar un concepto usando otros conceptos ya conocidos.
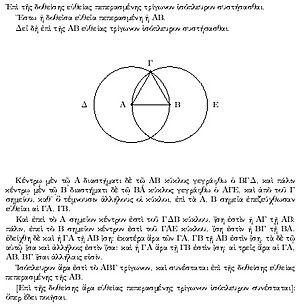
Las demostraciones en matemáticas cambiaron mucho gracias a Euclides (alrededor del 300 a.C.). Él introdujo el sistema axiomático, que todavía se usa hoy. Este método empieza con términos indefinidos y axiomas (ideas que se aceptan como verdaderas). A partir de ellos, se usan reglas de lógica deductiva para probar teoremas. Su libro, Los elementos, fue muy importante y se usó para educar a la gente en Occidente durante miles de años. En este libro, además de teoremas de geometría como el teorema de Pitágoras, Euclides demostró que la raíz cuadrada de dos es un número irracional y que hay infinitos números primos.
Más tarde, los matemáticos en el mundo islámico medieval también hicieron grandes avances. Mientras que las demostraciones griegas eran principalmente geométricas, los matemáticos islámicos desarrollaron la aritmética y el álgebra, lo que permitió demostraciones más generales que no dependían solo de dibujos. Por ejemplo, en el siglo X, el matemático Al-Hashim dio demostraciones generales para números, no solo para figuras geométricas.
Al-Karaji introdujo la demostración inductiva para secuencias aritméticas en el año 1000 d.C. También se usó para probar el teorema del binomio. Alhazen también desarrolló la demostración por contradicción.
Hoy en día, la teoría moderna de demostraciones ve las demostraciones como estructuras de datos. Los axiomas ya no se asumen como "verdaderos" en un sentido absoluto, lo que permite crear diferentes teorías matemáticas con distintos conjuntos de axiomas.
¿Para qué sirven las demostraciones?
Una demostración se escribe para convencer a quienes la leen de que una afirmación es verdadera. El nivel de detalle y rigor puede variar, pero siempre debe ser un argumento sólido.
En la lógica matemática, una demostración formal se escribe usando un lenguaje formal con símbolos, en lugar de palabras. Esto permite estudiar las propiedades de las demostraciones. Por ejemplo, la teoría de demostraciones puede mostrar que algunas afirmaciones no pueden ser demostradas.
Las demostraciones también pueden ser vistas como algo hermoso. El matemático Paul Erdős decía que las demostraciones más elegantes parecían venir de "El Libro", un texto imaginario que contendría las formas más bellas de probar cada teorema.
Tipos de demostraciones
No hay una única forma de demostrar algo, pero existen varios métodos comunes en matemáticas:
Demostración directa
En una demostración directa, se parte de una afirmación inicial (la hipótesis) y se llega a una conclusión (la tesis) usando lógica, axiomas, definiciones y teoremas que ya se conocen.
Por ejemplo, para demostrar que la suma de dos números enteros pares siempre es par:
- Imagina dos números pares, x e y.
- Como son pares, podemos escribirlos como x = 2a e y = 2b, donde a y b son números enteros.
- Su suma es x + y = 2a + 2b = 2(a + b).
- Como 2(a + b) tiene un factor de 2, significa que es un número par.
- Por lo tanto, la suma de dos números pares es par.
Demostración por inducción matemática
La inducción matemática no es como el razonamiento inductivo normal. En este tipo de demostración, se prueba que una afirmación es cierta para un primer caso (el "caso base"). Luego, se demuestra una "regla de inducción": si la afirmación es cierta para un caso, entonces también lo es para el siguiente. Al aplicar esta regla repetidamente, se demuestra que la afirmación es cierta para muchos casos, a veces infinitos.
Por ejemplo, para demostrar que todos los números de la forma 2n + 1 son impares (para n = 1, 2, 3...):
- Paso 1 (Caso base): Comprobamos para n = 1. Si n = 1, 2n + 1 = 2(1) + 1 = 3. Y 3 es impar. Así que es cierto para n = 1.
- Paso 2 (Regla de inducción): Suponemos que 2n + 1 es impar para algún número n. Ahora, veamos qué pasa con el siguiente número, n+1: 2(n+1) + 1 = (2n + 1) + 2. Si 2n + 1 es impar, al sumarle 2, el resultado sigue siendo impar. Así que, si es cierto para n, también lo es para n+1.
- Conclusión: Como es cierto para el primer caso y se cumple la regla de inducción, la afirmación "2n + 1 es impar" es verdadera para todos los números naturales.
Demostración por contraposición
La demostración por contraposición se basa en la idea de que si una afirmación "si P, entonces Q" es verdadera, entonces su "contrapositiva" "si no Q, entonces no P" también lo es.
Un ejemplo matemático: para demostrar que si a² es impar, entonces a es impar.
- Sabemos que si a es par, entonces a² es par (porque par x par = par).
- La contrapositiva de esto es: si a² no es par (es decir, es impar), entonces a no es par (es decir, es impar).
- Así, hemos demostrado que si a² es impar, entonces a es impar.
Demostración por reducción al absurdo
En la demostración por contradicción (también llamada reductio ad absurdum), se asume que la afirmación que queremos probar es falsa. Luego, se sigue razonando lógicamente hasta llegar a una contradicción (algo que no puede ser cierto). Como la suposición inicial nos llevó a una contradicción, significa que nuestra suposición era falsa, y por lo tanto, la afirmación original debe ser verdadera.
Un ejemplo famoso demuestra que la raíz cuadrada de dos es un número irracional:
- Supongamos que la raíz cuadrada de 2 es un número racional. Esto significa que se puede escribir como una fracción a/b, donde a y b son números enteros sin factores comunes (no se pueden simplificar más).
- Si (raíz de 2) = a/b, entonces 2b² = a².
- Esto significa que a² es un número par, lo que implica que a también debe ser par. Podemos escribir a = 2c (donde c es otro entero).
- Sustituyendo en la ecuación: 2b² = (2c)² = 4c².
- Dividiendo por 2: b² = 2c².
- Esto significa que b² es par, lo que implica que b también debe ser par.
- Pero si a y b son ambos pares, entonces ambos tienen un factor de 2. ¡Esto contradice nuestra suposición inicial de que a y b no tenían factores comunes!
- Como llegamos a una contradicción, nuestra suposición de que la raíz cuadrada de 2 es racional debe ser falsa. Por lo tanto, la raíz cuadrada de 2 es un número irracional.
Demostración constructiva
En una demostración constructiva, se muestra que algo existe construyendo un ejemplo específico de ello. Por ejemplo, Joseph Liouville demostró que existen los números trascendentales (números que no son solución de ninguna ecuación polinómica con coeficientes enteros) al construir un ejemplo de uno de ellos.
También se puede usar para construir un "contraejemplo" que demuestre que una afirmación no es cierta para todos los casos.
Demostración por exhaustividad
En este método, la demostración se divide en un número limitado de casos, y se prueba cada caso por separado. A veces, el número de casos puede ser muy grande. Por ejemplo, la primera demostración del teorema de los cuatro colores (que dice que cualquier mapa se puede colorear con solo cuatro colores sin que dos regiones vecinas tengan el mismo color) tuvo 1936 casos. Esta demostración fue un poco polémica porque la mayoría de los casos se verificaron con un programa de computadora.
Demostración probabilística
Una demostración probabilística muestra que un ejemplo existe con certeza, usando ideas de la teoría de probabilidad. No se debe confundir con decir que un teorema es "probablemente" cierto. Este tipo de demostración es una forma de demostrar teoremas de existencia.
Demostración no constructiva
Una demostración no constructiva establece que un objeto matemático con una cierta propiedad existe, pero sin mostrar cómo encontrarlo. A menudo, estas demostraciones usan el método de reducción al absurdo.
Un ejemplo famoso de demostración no constructiva muestra que existen dos números irracionales a y b tales que a elevado a la b es un número racional:
- Consideremos el número (raíz de 2) elevado a la (raíz de 2).
- Si este número es racional, entonces ya hemos encontrado nuestro ejemplo (a = raíz de 2, b = raíz de 2).
- Si este número es irracional, entonces podemos tomar a = (raíz de 2) elevado a la (raíz de 2) y b = raíz de 2.
- Entonces, a elevado a la b sería ((raíz de 2) elevado a la (raíz de 2)) elevado a la (raíz de 2), lo cual es igual a (raíz de 2) elevado a la 2, que es 2. Y 2 es un número racional.
- En ambos casos, hemos demostrado que existen dos números irracionales a y b tales que a elevado a la b es racional, sin decir exactamente cuáles son.
Demostraciones asistidas por computadora
Desde el siglo XX, las computadoras se usan para ayudar a probar teoremas y hacer cálculos que serían demasiado largos para los humanos. La primera demostración del teorema de los cuatro colores fue asistida por computadora. Algunos matemáticos se preocupan por la posibilidad de errores en los programas, pero en la práctica, se usan varias técnicas para reducir esos riesgos.
Afirmaciones que no se pueden decidir
Una afirmación que no se puede demostrar como verdadera ni como falsa a partir de un conjunto de axiomas se llama indecidible. Un ejemplo es el postulado de las paralelas en la geometría euclidiana, que no se puede probar ni refutar con los otros axiomas.
Los matemáticos han descubierto que muchos sistemas de axiomas importantes tienen afirmaciones indecidibles. El primer teorema de la incompletitud de Gödel muestra que esto es común en muchos sistemas matemáticos.
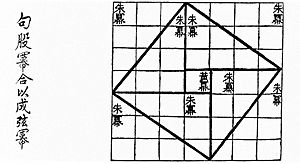
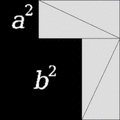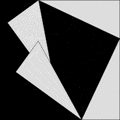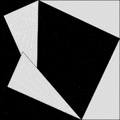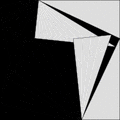
Demostraciones visuales
A veces, una "demostración sin palabras" es una imagen que ayuda a entender por qué un teorema es cierto, aunque no sea una demostración formal. La imagen de la derecha muestra una demostración visual del Teorema de Pitágoras para un triángulo con lados de 3, 4 y 5.
¿Cómo termina una demostración?
Al final de una demostración, a veces se escribe la abreviación QED. Esto viene del latín quod erat demonstrandum, que significa "lo que se quería demostrar". Una forma más común hoy en día es usar un cuadrado o un rectángulo, como □ o ∎, también conocidos como "tombstone" o "halmos".
Galería de imágenes
Véase también
 En inglés: Mathematical proof Facts for Kids
En inglés: Mathematical proof Facts for Kids